高三复习数学试题
时间:120分钟 满分:150分 命题人:彭 放
【一】选择题(本大题共10小题,每小题5分,共50分)
1.在![]() 中, 已知
中, 已知![]() ,则角
,则角![]() 的度数为 ( )
的度数为 ( )
A.
![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.在数列![]() 中,
中,![]() =1,
=1,![]() ,则
,则![]() 的值为
( )
的值为
( )
A.99 B.49 C.101 D. 102
3.已知![]() ,函数
,函数![]() 的最小值是
( )
的最小值是
( )
A.5 B.4 C.8 D.6
4.(文科选做)在等比数列中,![]() ,
,![]() ,
,![]() ,则项数
,则项数![]() 为 (
)
为 (
)
A. 3 B. 4 C. 5 D. 6
(理科选做)各项均为正数的等比数列![]() 的前n项和为Sn,若
的前n项和为Sn,若![]() =2,
=2,![]() =14,则
=14,则![]() 等于
等于
A.80 B.26 C.30 D.16
5.不等式![]() 的解集是
( )
的解集是
( )
A. ![]() B.
B.
![]()
C. ![]() D.
D. ![]()
6.设满足约束条件
,则
的最大值为 ( )
A. 5 B. 3 C. 7 D. -8
7.不等式![]() 的解集为
的解集为![]() ,那么
( )
,那么
( )
A.B.
C.
D.
8.![]() 中,若
中,若![]() ,则
,则![]() 的面积为
( )
的面积为
( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
9.
等差数列![]() 的前
的前![]() 项和为20,前
项和为20,前![]() 项和为70,则它的前
项和为70,则它的前![]() 的和为( )
的和为( )
A. 130 B. 150 C. 170 D. 210
10.在等比数列![]() 中,公比q=2,且
中,公比q=2,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C
C![]() D
D![]()
【二】填空题(本大题共4小题,每小题5分,共20分,其中14题任选一题作答,都做只计A题分数)
11.(文科选做) 等差数列![]() 中,已知
中,已知![]() ,那么
,那么![]() 的值是__________.
的值是__________.
(理科选做)若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 ;数列
,则此数列的通项公式为 ;数列![]() 中数值最小的项是第 项.
中数值最小的项是第 项.
12. 在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() __________.
__________.
13.若不等式![]() 的解为
的解为![]() 则
则![]() ,
,![]() .
.
14(A).定义一种新的运算“![]() ”对任意正整数n满足下列两个条件:(1)
”对任意正整数n满足下列两个条件:(1)![]()
![]() 则
则![]() ____________
____________
14(B).若对于一切正实数![]() 不等式
不等式![]() >
>![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
数学试题(答卷)
时间:120分钟 满分:150分 命题人:彭 放
【一】选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
【二】填空题(本大题共4小题,每小题5分,共20分,其中14题任选一题作答,都做只计A题分数,13题第一空3分,第二空2分)
11. , 12.
13.![]() ,
,![]() 14(A).
(B).
14(A).
(B).
【三】解答题(本大题共6个小题,共80分;解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分12分)已知等比数列![]() 中,
中,![]() ,求其第4项及前5项和.
,求其第4项及前5项和.
16.(本小题满分14分)求下列不等式的解集:(1)![]()
(2)(文科选做)![]() (理科选做)
(理科选做) ![]()
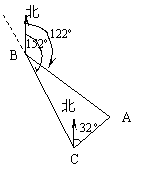
17.(本小题满分12分)如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为![]() 的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为
的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为![]() .半小时后,货轮到达C点处,观测到灯塔A的方位角为
.半小时后,货轮到达C点处,观测到灯塔A的方位角为![]() .求此时货轮与灯塔之间的距离.
.求此时货轮与灯塔之间的距离.
 |
18.(本小题满分14分)在![]() 中,
中,![]() 分别为
分别为![]() 的对边,已知
的对边,已知![]() 成等比数列,且
成等比数列,且![]() .求:(1)A的大小;(2)
.求:(1)A的大小;(2)![]() 的值.
的值.
19.(本小题满分14分)某厂用甲、乙两种原料生产A、B两种产品,已知生产1t A产品,1t B产品分别需要的甲、乙原料数,可获得的利润数及该厂现有原料数如下表所示.问:在现有原料下,A、B产品应各生产多少才能使利润总额最大?列产品和原料关系表如下:
|
| A产品 (1t) | B产品 (1t) | 总原料 (t) | ||
| 甲原料(t) | 2 | 5 | 10 | ||
| 乙原料(t) | 6 | 3 | 18 | ||
| 利润(万元) | 4 | 3 |
20.(文科选做)(本小题满分14分)已知![]() 为等差数列,且
为等差数列,且![]() .
.
(1)求数列![]() 的通项公式; (2)令
的通项公式; (2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(理科选做)数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项
的通项![]() ;
;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【一】选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | B | C | A | C | A | B | B | B |
【二】填空题(本大题共4小题,每小题5分,共20分,其中14题任选一题作答,都做只计A题分数,11、13题第一空3分,第二空2分)
11.文科 60 理科 ![]()
![]() 12. 7
12. 7
13.![]() -6 ,
-6 ,![]() 1 14(A). 4011 (B). a<
1 14(A). 4011 (B). a<![]()
15.解:设公比为![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分
由已知得 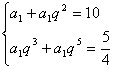 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 3分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 3分
|
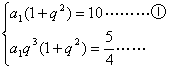 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 5分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 5分
②÷①得 ![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7分
将![]() 代入①得
代入①得 ![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
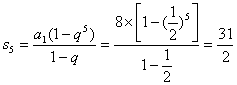 ┄┄┄┄┄┄┄┄┄┄ 12分
┄┄┄┄┄┄┄┄┄┄ 12分
16.解:(1)方程![]() 的两解为
的两解为![]() ,根据函数图像可知原不等式
,根据函数图像可知原不等式![]() 的解为
的解为![]() ┄┄┄┄┄ 7分
┄┄┄┄┄ 7分
(2)(文科选做)方程![]() 的两解为
的两解为![]() ,根据函数图像可知原不等式
,根据函数图像可知原不等式![]() 的解为
的解为![]() ┄┄┄┄┄ 14分
┄┄┄┄┄ 14分
(理科选做)解:原不等式等价于:
![]()
![]() 或
或![]()
∴原不等式的解集为![]() ┄┄┄┄
14分
┄┄┄┄
14分
17.在△ABC中,∠B=152o-122o=30o,∠C=180o-152o+32o=60o,∠A=180o-30o-60o=90o,┄┄┄┄┄(4分)
BC=![]() ,┄┄┄┄┄(6分)
,┄┄┄┄┄(6分)
∴AC=![]() sin30o=
sin30o=![]() .┄┄┄┄┄(12分)
.┄┄┄┄┄(12分)
答:船与灯塔间的距离为![]() n mile.
n mile.
18.解析:由已知得![]() ,
,
因此![]() 可化为
可化为![]() ……3分
……3分
![]()
![]() ………………………7分
………………………7分
![]() 法一:在
法一:在![]() 中,由正弦定理得
中,由正弦定理得![]()
![]() ………………………………10分
………………………………10分
![]() .……………………14分
.……………………14分
法二:在![]() 中,由面积公式得
中,由面积公式得![]() .
.
![]()
![]()
![]() .…………14分
.…………14分
19.(14分)[解析]:设生产A、B两种产品分别为xt,yt,其利润总额为z万元,
根据题意,可得约束条件为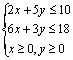 ……3分
……3分
 作出可行域如图: ….5分
作出可行域如图: ….5分
 目标函数z=4x+3y,
目标函数z=4x+3y,
作直线l0:4x+3y=0,再作一组平行于l0的直线l: 4x+3y =z,当直线l经过P点时z=4x+3y取得最大值, …….9分
由![]() ,解得交点P
,解得交点P![]() …….12分
…….12分
所以有![]() ………13分
………13分
所以生产A产品2.5t,B产品1t时,总利润最大,为13万元.………14分
20.(文科选做)解:(1)设为等差数列![]() 的公差为d,则
的公差为d,则
∴ ![]()
∴ d = 2
∴ ![]() …………5分
…………5分
(2)![]()
![]() ①
①
4![]() ②…………7分
②…………7分
②-①得
3![]() … 8分
… 8分
=![]() … ………10分
… ………10分
=![]() ……11分
……11分
∴ ![]() ………14分
………14分
(理科选做)解:(Ⅰ)![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() .
.
当![]() 时,
时,![]() ,
,
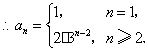 ………………… 5分
………………… 5分
(Ⅱ)![]() ,………………………6分
,………………………6分
当![]() 时,
时,![]() ;………………………7分
;………………………7分
当![]() 时,
时,![]() ,…………①
,…………①
![]() ,………………………②………………………9分
,………………………②………………………9分
![]() 得:
得:![]()
![]()
![]() .………………………12分
.………………………12分
![]() .………………………13分
.………………………13分
又![]() 也满足上式,
也满足上式,
![]() . ………14分
. ………14分
