高三理科数学下学期期中试题
（）
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．复数
等于（ ）
A．
B．
C．
D．
2．不等式
的解集是（ ）
A．
B．
C．
D．
3．设
是两个集合，则“
”是“
”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分又不必要条件
4．已知函数
,且对任意x都有
则
的最小正周期为（ ）
A．4 B．3 C．2 D．1
5．设随机变量
服从标准正态分布
，已知
，则
=（ ）
A．0.025 B．0.050 C．0.925 D．0.950
6．函数
的图象和函数
的图象的交点个数是（ ）
A．4 B．3 C．2 D．1
7．已知数列
,
的前n项和为（ ）
A.
B. 
C.
D.
8．随机抛掷一个材料均匀的骰子，所得骰子的点数的期望等于（ ）
A. 
B.
3.5
C. 6
D. 1
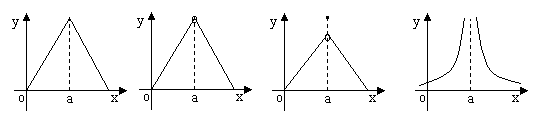
9．在下列图象所表示的函数中满足在点x＝a处有定义、有极限但不连续的是( )
A.
B.
C.
D.
10．甲、乙两台生产同一种零件的车床每天生产中分别出现次品数的分布列如下，如果两台车床的产量相同，判断哪台车床更好一些（ ）。
|
| 0 | 1 | 2 | 3 |
| 0 | 1 | 2 | 3 | |
| P | 0.3 | 0.5 | 0.2 | 0 | P | 0.4 | 0.3 | 0.2 | 0.1 |
A. 甲车床好些 B. 乙车床好些 C. 一样好 D. 无法比较
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题：本大题共5小题，每小题5分，共25分．把答案填在横线上．
11．已知函数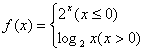
，则
的值等于____________。
12．若函数
，且它在x=1处的导数
=0，则a的值等于_____________。
13．函数
在区间
上的最小值是 ．
14．求曲线
在点P
处的切线方程 。
15．用数学归纳法证明某命题：若“n＝k时，左边＝
”，则“从n＝k到n＝k＋1”，左边多填加的项是______________________
三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．
16．（本小题满分12分）
等差数列{an}中，若a5=10，S3=3。求：
（1）数列的通项公式；
（2）数列的前10项和。
17. （本小题满分12分）
已知集合A={xx2-3x+2=0}，B={xx2-mx+2=0}，且A∩B=B，求实数m的取值范围。
18．（本小题满分12分）
某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响．
（I）任选1名下岗人员，求该人参加过培训的概率；
（II）任选3名下岗人员，记为3人中参加过培训的人数，求的分布列和期望．
19．（12分）据统计，某种型号的汽车在匀速行驶中每小时的耗油量y（升）与汽车行驶速度x（千米/小时）之间的函数关系可以表示为
，已知甲、乙两地相距100千米。问：汽车以多大的速度匀速行驶时，从甲地到乙地的耗油量
最少？最少为多少升？
20．（本小题满分12分）
函数f(x)=ax3+bx2+cx (a≠0)在x=±1时取得极值，且f(1)= -1
（1）求常数a、b、c的值；
（2）求函数f(x)的单调区间及极值。
21．（本小题满分13分）
已知
（
）是曲线
上的点，
，
是数列
的前
项和，且满足
，
，
…．
（I）证明：数列
（
）是常数数列；
（II）确定
的取值集合
，使
时，数列是单调递增数列；
（III）证明：当时，弦
（）的斜率随单调递增．
数学（高三理科）
参考答案
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．C 2．D 3．B 4．A 5．D 6．C 7．B 8．B 9．C 10．A
二、填空题：本大题共5小题，每小题5分，共25分．把答案填在横线上．
11．1/4
12．1
13．
14．
15．
三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．
16解：设等差数列首项为a1，公差为d. 则由题可知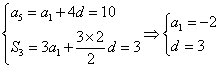
(1)所以数列的通项公式
(2) 数列的前十项和
17．化简条件得A={1，2}，A∩B=B
B
A,
根据集合中元素个数集合B分类讨论，B=φ，B={1}或{2}，B={1，2}
当B=φ时，△=m2-8<0
∴
当B={1}或{2}时，
，m无解;
当B={1，2}时，
∴ m=3
综上所述，m=3或.
18．(2007湖南理)解：任选1名下岗人员，记“该人参加过财会培训”为事件
，“该人参加过计算机培训”为事件
，由题设知，事件与相互独立，且
，
．
（I）解法一：任选1名下岗人员，该人没有参加过培训的概率是
所以该人参加过培训的概率是
．
解法二：任选1名下岗人员，该人只参加过一项培训的概率是
该人参加过两项培训的概率是
．
所以该人参加过培训的概率是
．
（II）因为每个人的选择是相互独立的，所以3人中参加过培训的人数服从二项分布
，
，
，即的分布列是
|
| 0 | 1 | 2 | 3 |
|
| 0.001 | 0.027 | 0. 243 | 0.729 |
的期望是
．
（或的期望是
）
19．解：当速度为x（千米/小时）时，汽车从甲地到乙地行驶用时为
小时，
则有
令
解得
当
时，
，函数是减函数；
当
时，
，函数是增函数
所以当x=80时，函数取到极小值
因为函数在区间
上只有一个极小值，所以它就是最小值
答：当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油量最少，
最少为11.25升。
（本题也可以利用均值定理解题）
20． 解：（1）因为
，
所以由题可得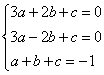 
，解得
……5分
（2）由（1）知
当
时，
，即函数在
单调递增；
当
时，
，函数在（－1，1）单调递减……10分
所以x＝－1时，函数取得极大值，f（－1）＝1
x＝1时，函数取得极小值，f（1）＝－1 12分
21．(2007湖南理)解：（I）当
时，由已知得
．
因为
，所以
．
…… ①
于是
．
……②
由②－①得
．
…… ③
于是
．
…… ④
由④－③得
，
…… ⑤
所以
，即数列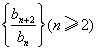
是常数数列．
（II）由①有
，所以
．由③有
，
，所以
，
．
而 ⑤表明：数列
和
分别是以
，
为首项，6为公差的等差数列，
所以
，
，
，
数列是单调递增数列
且
对任意的
成立．
且
．
即所求的取值集合是
．
（III）解法一：弦的斜率为
任取
，设函数
，则
记
，则
，
当
时，
，
在
上为增函数，
当
时，
，在
上为减函数，
所以
时，
，从而
，所以在和上都是增函数．
由（II）知，时，数列单调递增，
取
，因为
，所以
．
取
，因为，所以
．
所以
，即弦
的斜率随单调递增．
解法二：设函数
，同解法一得，在
和
上都是增函数，
所以
，
．
故，即弦的斜率随单调递增．