高三数学综合测试题(5)
(理科)
总分150分
一.选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只 有一项是符合题目要求的.请把答案填在答题卡上.
1.P是△ABC所在平面上一点,若![]() ,则P是△ABC的
,则P是△ABC的
A 外心 B 内心 C 重心 D 垂心
2.直线l经过A(2,1)、B(1,m2)(m∈R)两点,那么直线l的倾斜角的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知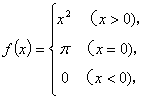 则
则![]() 的值等于( )
的值等于( )
A.0 B.![]() C.
C.![]() D.9
D.9
4.已知![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在R上定义运算![]() :
:![]() .若不等式
.若不等式![]() 对任意实数
对任意实数![]() 成立,则
成立,则![]() 的取值范围 ( )
的取值范围 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
6.要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象作下列变换,其中正确的变换是 ( )
的图象作下列变换,其中正确的变换是 ( )
A.先纵坐标不变,横坐标缩短原来的![]() 再按向量(
再按向量(![]() )平移
)平移
B.先纵坐标不变,横坐标缩短原来的![]() 再按向量(
再按向量(![]() )平移
)平移
C.先按向量(![]() )平移,再纵坐标不变,横坐标缩短原来的
)平移,再纵坐标不变,横坐标缩短原来的![]()
D.先按向量(![]() )平移,再纵坐标不变,横坐标缩短原来的
)平移,再纵坐标不变,横坐标缩短原来的![]()
7.设![]() 是定义在实数集
是定义在实数集![]() 上以2为周期的奇函数,已知
上以2为周期的奇函数,已知![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上( )
上( )
A.是减函数,且![]() ; B.是增函数,且
; B.是增函数,且![]() ;
;
C.是减函数,且![]() D.是增函数,且
D.是增函数,且![]() ;
;
8. 由动点P向圆x2 + y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为 ( )
A x2+y2=4 B x2+y2=3 C x2+y2=2 D x2+y2=1
二.填空题:本大题共6小题,每小题5分,共30分.请将答案填在答卷相应的横线上.
9.半径为5的圆过点A(-2, 6),且以M(5, 4)为中点的弦长为2![]() ,则此圆的方程是 。
,则此圆的方程是 。
10.已知函数![]() 的值域为R,则实数
的值域为R,则实数![]() 的取值范围是 .
的取值范围是 .
11.已知向量![]() ,且A、B、C三点共线,则k=_ __
,且A、B、C三点共线,则k=_ __
12.已知点A(2,0),B(4,0),动点P在抛物线y2=-4x运动,则使![]() 取得最小值的点P的坐标是
.
取得最小值的点P的坐标是
.
13.过点![]() (1,2)的直线l将圆
(1,2)的直线l将圆![]() 分成两段弧,其中的劣弧最短时,l的方程为
.
分成两段弧,其中的劣弧最短时,l的方程为
.
14. 海上有A、B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,那么B岛和C岛间的距离是 海里.
三、解答题:本大题共6小题,共80分.写出简要答案与过程。
15.(本题12分)已知△ABC中,∠C=120°,c=7,a+b=8,求![]() 的值。
的值。
16(本题13分)已知![]() 是二次函数,方程
是二次函数,方程![]() 有两相等实根,且
有两相等实根,且![]()
(1)求![]() 的解析式.
的解析式.
(2)求函数![]() 与函数
与函数![]() 所围成的图形的面积.
所围成的图形的面积.
17.( 本题13分)已知点A、B、C的坐标分别为A(3,0),B(0,3),C(cosα,sinα),α![]() (
(![]() )。
)。
(1)若![]() ,求角α的值;
,求角α的值;
| |
18. 已知定点A(0,1),B(0,-1),C(1,0)。动点P满足:![]() 。
。
(1)求动点P的轨迹方程,并说明方程表示的曲线;(2)当![]() 的最大值和最小值。
的最大值和最小值。
19.(本题14分)设函数![]() (
(![]() )的图象关于原点对称,且
)的图象关于原点对称,且![]() 时,
时,![]() 取极小值
取极小值![]()
①求![]() 的值;
的值;
②当![]() 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
③若![]() ,求证:
,求证:![]() 。
。
20.(本题14分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,且过点
的图象上,且过点![]() 的切线的斜率为
的切线的斜率为![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() ;
;
(Ⅲ)设![]() ,
,![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,
中的最小数,![]() ,求
,求![]() 的通项公式.
的通项公式.
高三级数学(5)(理科)
一.D D C B D A B A
二.9:(x-1)2+(y-2)2=25或(x-![]() )2+(y-
)2+(y-![]() )2=25 10:
)2=25 10:![]()
11:![]() 12:(0,0) 13:
12:(0,0) 13:![]() 14 :5
14 :5
三、解答题
15.解:由正弦定理:![]() ,…………………………3分
,…………………………3分
代入![]() …7分
…7分
![]() ………………………10分
………………………10分
∴![]() ………………………………………12分
………………………………………12分
16.解:(1)设![]() .
.
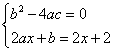 ----------------------- 4分
----------------------- 4分
得:![]()
![]() ----------------------- 6分
----------------------- 6分
(2)由题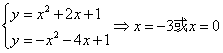 ------------------- 8分
------------------- 8分
![]() ------------------- 10分
------------------- 10分
![]()
=9 ------------------------------------------------------- 13分
17.解:解:(1)∵![]() =(cos
=(cos![]() -3, sin
-3, sin![]() ),
), ![]() =(cos
=(cos![]() , sin
, sin![]() -3). ……2分
-3). ……2分
∴∣![]() ∣=
∣=![]() 。
。
∣![]() ∣=
∣=![]() 。………………………4分
。………………………4分
由∣![]() ∣=∣
∣=∣![]() ∣得sin
∣得sin![]() =cos
=cos![]() .又∵
.又∵![]()
![]() ,∴
,∴![]() =
=![]() ……6分
……6分
(2)由![]() ·
·![]() =-1,得(cos
=-1,得(cos![]() -3)cos
-3)cos![]() +sin
+sin![]() (sin
(sin![]() -3)=-1
-3)=-1
∴ sin![]() +cos
+cos![]() =
=![]() .① ………………………………………………8分
.① ………………………………………………8分
又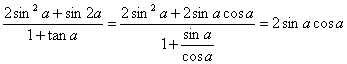 .
.
由①式两边平方得1+2sin![]() cos
cos![]() =
=![]() , ∴2sin
, ∴2sin![]() cos
cos![]() =
=![]() , ………12分
, ………12分
∴![]() ………………………………………………13分
………………………………………………13分
18解:(1)设动点的坐标为P(x,y),则![]() =(x,y-1),
=(x,y-1),![]() =(x,y+1),
=(x,y+1),![]() =(1-x,-y)
=(1-x,-y)
∵![]() ·
·![]() =k
=k![]() 2,∴x2+y2-1=k[(x-1)2+y2]
2,∴x2+y2-1=k[(x-1)2+y2]
即(1-k)x2+(1-k)y2+2kx-k-1=0。
若k=1,则方程为x=1,表示过点(1,0)是平行于y轴的直线。
若k≠1,则方程化为:![]() ,
,
表示以(-![]() ,0)为圆心,以
,0)为圆心,以![]() 为半径的圆。
为半径的圆。
(2)当k=2时,方程化为(x-2)2+y2=1。∵2![]() +
+![]() =2(x,y-1)+(x,y+1)=(3x,3y-1),
=2(x,y-1)+(x,y+1)=(3x,3y-1),
∴2![]() +
+![]() =
=![]() 。又x2+y2=4x-3,
。又x2+y2=4x-3,
∴2![]() +
+![]() =
=![]() ∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。
∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。
则36x-6y-26=36cosθ-6sinθ+46=6![]() cos(θ+φ)+46∈[46-6
cos(θ+φ)+46∈[46-6![]() ,46+6
,46+6![]() ],
],
∴2![]() +
+![]() max=
max=![]() =3+
=3+![]() ,2
,2![]() +
+![]() min=
min=![]() =
=![]() -3。
-3。
19.解:①![]() 函数
函数![]() 的图象关于原点对称
的图象关于原点对称
![]() 对任意实数
对任意实数![]() ,有
,有![]()
![]()
![]() …………………………………3分
…………………………………3分
即![]() 恒成立
恒成立
![]()
![]()
![]()
![]() 时,
时,![]() 取极小值
取极小值![]() ,
,![]() 且
且![]() ,
,
![]() …………………………………………………………………………5分
…………………………………………………………………………5分
②当![]() 时,图象上不存在这样的两点使结论成立。
时,图象上不存在这样的两点使结论成立。
假设图象上存在两点![]() ,使得过此两点处的切线互相垂直,则由
,使得过此两点处的切线互相垂直,则由![]() 知两点处的切线斜率分别为
知两点处的切线斜率分别为![]() …………………………………………… …6分
…………………………………………… …6分
且![]() (*)
(*)
![]() [-1,1]
[-1,1]![]() 与(*)矛盾………………………………9分
与(*)矛盾………………………………9分
③![]() 令
令![]() 得
得![]() ,
,![]()
或![]() 时,
时,![]() ,
,
![]() 时
时![]()
![]()
![]() 在[-1,1]上是减函数,且
在[-1,1]上是减函数,且![]() …………………………11分
…………………………11分
![]()
![]() 在[-1,1]上
在[-1,1]上![]()
![]() 时,
时,![]() ………………14分
………………14分
20(本题14分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,且过点
的图象上,且过点![]() 的切线的斜率为
的切线的斜率为![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() ;
;
(Ⅲ)设![]() ,
,![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,
中的最小数,![]() ,求
,求![]() 的通项公式.
的通项公式.
20. 解:(Ⅰ)因为点![]() 都在函数
都在函数![]() 的图象上
的图象上
所以![]()
![]()
当![]() 时,
时,![]() ------------------ 2分
------------------ 2分
当![]() 时,
时,![]() (*)------- 3分
(*)------- 3分
令![]() ,
,![]() ,也满足(*)式
,也满足(*)式
所以,数列![]() 的通项公式是
的通项公式是![]() . -------------- 4分
. -------------- 4分
(Ⅱ)由![]() 求导可得
求导可得
![]()
∵ 过点![]() 的切线的斜率为
的切线的斜率为![]()
∴ ![]() -------------
------ 6分
-------------
------ 6分
又∵![]()
∴![]() -------------- 7分
-------------- 7分
∴ ![]()
![]() ① 由①
① 由①![]() 可得
可得
![]()
![]() ②
②
①-②可得
![]()
![]()
![]()
![]()
∴ ![]() -------------- 9分
-------------- 9分
(Ⅲ)∵![]() ,
,![]()
∴![]() --------------------------- 10分
--------------------------- 10分
又∵![]() ,其中
,其中![]() 是
是![]() 中的最小数,
中的最小数,
∴![]() , --------------------------- 11分
, --------------------------- 11分
∴ ![]()
![]() (
(![]() 的公差是4 的倍数!)
的公差是4 的倍数!)
又∵![]()
∴![]() 解得
解得![]()
∴![]() --------------------------- 12分
--------------------------- 12分
设等差数列![]() 的公差为
的公差为![]()
则![]()
∴ ![]()
所以,![]() 的通项公式为
的通项公式为![]() . -------------------------- 14分
. -------------------------- 14分