高三数学综合练习（二）
总分１５０分
一、选择题（每题5分，共50分，请将答案填涂在答题卡上）
1、设全集U=R，A={xx＞2}，B={xx2－4x＋3＜0}，则A∩(CUB)是……………………………（ ）
(A){xx＜－2} (B){xx＜－2或x≥3} (C) {xx≥3} (D){x－2≤x＜3}
2、“直线l在y轴上的截距是在x轴上的截距的2倍”是“直线l的斜率等于－2”的…………（ ）
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
3、函数y=f(x)的图象与y=2x的图象关于y轴对称，若y=f -1(x)是y=f (x)的反函数，则y=f -1(x2－2x)的单调递增区间是………………………………………………………………………………（ ）
(A) [1，+∞) (B) (2，+∞) (C) (－∞，1] (D)(－∞，0)
4、已知等差数列{an}的首项a1=120，d=－4，记Sn= a1＋a2＋…＋an，若Sn≤an（n＞1），则n最小值为……………………………………………………………………………………………（ ）
(A)60 (B)62 (C)63 (D)70
5、半径为4的球面上有A、B、C、D四点，且满足·＝0, ·＝0，·＝0，则S△ABC＋S△ACD＋S△ADB的最大值为（S为三角形的面积）…………………………………（ ）
(A)8 (B)16 (C)32 (D)64
6、正四棱锥的一个对角面的面积是一个侧面面积的倍，则侧面与底面所成角为 …（ ）
(A) (B) (C) (D)
7、已知x、y∈R，且x＋2y≥1，则式u=x2＋y2＋4x－2y的最小值为 ………………（ ）
(A)－3 (B) (C)24 (D)－
8、某班有48名学生，某次数学考试，算术平均分为70分，标准差为s，后来发现成绩记录有误，某甲得80分却误记为50分，某乙得70分却误记为100分，更正后计算得标准差为s1，则s1和s之间的大小关系为 …………………………………………………………………（ ）
(A) s1＞s (B) s1＝s (C) s＋5＜s1 (D) s＞s1
9、从6人中选4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览，要求每个城市有一人游览，每个人只能游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有（ ）
(A)300种 (B)240种 (C)144种 (D)96种
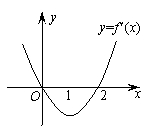
10、设f' (x)是函数f (x)的导函数，y= f' (x)的图象如右图所示，则y=f (x)
的图象最有可能是…（ ）
 |
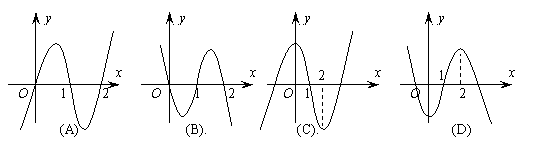二、填空题（每题5分，共30分，请将答案填在答案卷题号相应处）
11、设等比数列{an}的前n项和为Sn，若S6:S3＝1:2，则S9:S3＝ ▲ .
12、cos75°－cos15°的值等于 ▲ .
13、在(－)n的展开式中，只有第5项的二项式系数最大，则展开式中常数项是 ▲ .
 |
14、如图，在一个木制的棱长为3的正方体表面涂上颜色，
将它的棱三等分，然后从等分点把正方体锯开，得到27个
棱长为一的小正方体，将这些小正方体充分混合后，装入一
个口袋中.从口袋中同时任意取出2个小正方体，其中1个小
正方体恰好有1个面涂有颜色，另一个小正方体至少有两个
面涂有颜色的概率是 ▲ .
15、设双曲线－＝1(a＞0，b＞0)的右焦点为F，右准线l与两条渐近线交于P、Q两点，如果△PQF是直角三角形，则双曲线的离心率e= ▲ .
16、已知定义在R上的函数f(x)＝x2－2ax＋b（a,b∈R）.给出下列命题：
①f(x)必是偶函数；
②f(0)=f(2)时，f(x)的图象必关于直线x=1对称；
③若a2－b=0，则f(x)在区间[a，+∞)上是增函数；
④f(x)有最大值a2－b.
其中正确的命题的序号是 ▲ .
高三数学综合练习（二）
班级 学号 姓名
| 一、选择题（每题5分，共50分，请将答案填涂在答题卡上） |
| 二、填空题（每题5分，共30分，请将答案填在答案卷题号相应处） 11、 12、 13、 14、 15、 16、 |
| 三、解答题（共5题，满分70分） 17、（本题满分12分）设=(2cosx,sinx)，=(cosx,2cosx)，定义f(x)=·＋1＋m(m∈R). （1）求f(x)的最小正周期； （2）求f(x)的单调递减区间； （3）若当x∈[0，]时，f(x)的最小值为4，求m的值. |
|
（1）求证：四边形A B1C1D1为菱形； （2）求截面A B1C1D1与底面ABCD所成的二面角的大小； （3）求几何体ABCDD1C1B1的体积. |
|
（1）分别将A、B两产品的利润表示为投资量的函数关系式； （2）该公司已有10万元资金，并全部投入A、B两种产品， 问：怎样分配这10万元投资，才能使公司获得最大利
|
| 20、(本题满分14分)已知定点P(1,0)，动点Q满足比在x轴正方向上的投影多2. （1）求Q点的轨迹方程； （2）若O为原点，AB为动点Q的轨迹上两点，且△AOB的面积S=m·tan∠AOB， 求m的最小值； （3）当m取最小值时，若OR垂直AB于R，求R的轨迹方程. |
| 21、(本题满分16分)已知函数f(x)=，a∈R. （1）当x∈[a+1，a+2]时，求f(x)的取值范围； （2）证明：函数y=f(x)的图象关于点(a，－1)成中心对称图形； （3）我们利用函数y=f(x)构造一个数列{xn}，方法如下：对于给定的定义域中的x1，令x2=f(x1)，x3=f(x2)，…，xn=f(xn-1)，…上述构造数列的过程中，如果xi(i=2,3,4,…)在定义域中，构造数列的过程将继续下去，如果xi不在定义域中，则构造数列的过程停止. ①如果可以用上述方法构造出一个常数数列{xn}，求实数a的取值范围； ②如果取定义域中任一值作为x1，都可以用上述方法构造出一个无穷数列{xn}，求实数a的值. |
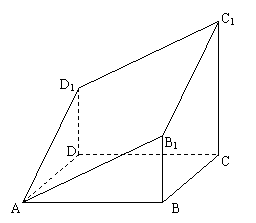18、（本题满分14分）经过底面是菱形的直四棱柱ABCD－A'B'C'D'的顶点A作一截面AB1C1D1，分别与侧棱BB'、CC'、DD'交于点B1、C1、D1，得到几何体ABCDD1C1B1（如图），若BB1=DD1，CC1=，AB=2，∠DAB=60°.
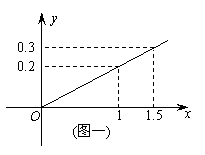19、（本题满分14分）某公司计划投资A、B两种金融产品，根据市场调查和预测，A产品的利润y与投资量x成正比例，其关系如图图(一)，B产品的利润y与投资量x的算术平方根成正比例，其关系如图图(二).(注：利润与投资量的单位：万元).
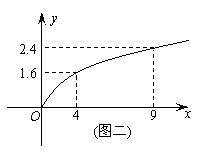润？其最大利润为多少元？