高三下学期数学模拟试题
参考公式:


第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.(理)若复数![]() 满足方程
满足方程![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)设![]() ,则下列不等式恒成立的是( )
,则下列不等式恒成立的是( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
3.(理)已知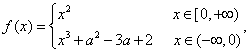 在
在![]() 上是增函数,则常数
上是增函数,则常数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(文)已知![]() 则
则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.在![]() 中,若
中,若![]() ,则这个三角形一定是( )
,则这个三角形一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
5.若向量![]() ,
,![]() ,则
,则![]() 一定满足( )
一定满足( )
 A.
A.![]() 的夹角等于
的夹角等于![]() B.
B.![]()
C.![]() D.
D.![]()
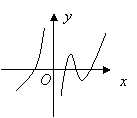
6.设函数![]() 在定义域内可导。函数
在定义域内可导。函数![]() 的图像如图,
的图像如图,
则导函数![]() 的图象可能为( )
的图象可能为( )
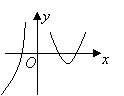
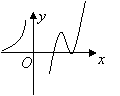
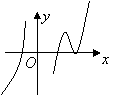
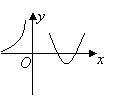
A. B. C. D.
7.三棱锥![]() 中,
中,![]() 、
、![]() 、
、![]() 两两互相垂直,且
两两互相垂直,且![]() ,
,![]() ,空间一点
,空间一点![]() 到点
到点![]() 、
、![]() 、
、![]() 、
、![]() 的距离均为
的距离均为![]() ,则
,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.要得到函数![]() 的图像,只需将函数
的图像,只需将函数![]() 的图象( )
的图象( )
A.向左平移![]() 个单位 B.向右平移
个单位 B.向右平移![]() 个单位
个单位
C.向左平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
9.已知等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.(理)函数极限![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.在![]() 的展开式中,各项系数和是( )
的展开式中,各项系数和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个数字,可以组成比
这五个数字,可以组成比![]() 大,并且百位数字不是数字
大,并且百位数字不是数字![]() 的没有重复数字的五位数,则这样的五位数共有( )
的没有重复数字的五位数,则这样的五位数共有( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分。)
13.某工厂生产![]() 、
、![]() 、
、![]() 三种不同型号的产品,产品数量之比依次为
三种不同型号的产品,产品数量之比依次为![]() 。现用分层抽样方法抽出一个容量为
。现用分层抽样方法抽出一个容量为![]() 的样本,样本中
的样本,样本中![]() 种型号产品有
种型号产品有![]() 件,那么此样本的容量
件,那么此样本的容量![]()
14.若![]() 、
、![]() ,且
,且![]() ,则
,则![]() 的最小值是
的最小值是
15.已知![]() ,函数
,函数![]() 的图象与
的图象与![]() 的图象关于
的图象关于![]() 对称,则
对称,则![]()
16.将正方形![]() 沿对角线
沿对角线![]() 折成直二面角
折成直二面角![]() ,有如下四个结论:
,有如下四个结论:
①![]() ;
;
②![]() 是等边三角形;
是等边三角形;
③![]() 与平面
与平面![]() 成
成![]() 角;
角;
④![]() 成
成![]() 角。
角。
其中正确结论的序号是
三、解答题(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤)
17.已知向量![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的最小值。
的最小值。
18.(理)已知甲、乙投篮一次投中的概率分别是![]() 。现甲、乙二人各投篮两次。
。现甲、乙二人各投篮两次。
(Ⅰ)求甲恰好投中两次、乙恰好投中一次的概率;
(Ⅱ)设甲、乙二人进球数之和为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
(文)已知甲、乙投篮一次投中的概率分别是![]() 。现甲、乙各投篮两次。
。现甲、乙各投篮两次。
(Ⅰ)求甲恰好投中两次、乙恰好投中一次的概率;
(Ⅱ)求甲进球数多于乙进球数的概率。
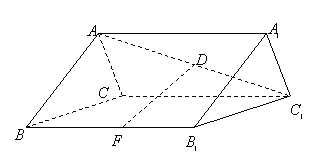 19.如图,正三棱柱
19.如图,正三棱柱![]() 的各棱长都等于
的各棱长都等于![]() ,
,![]() 在
在![]() 上、
上、![]() 为
为![]() 中点,且
中点,且![]() 。
。
(Ⅰ)求二面角![]() 的大小;
的大小;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离。
的距离。
20.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]()
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() 。求
。求![]() 的前
的前![]() 项和
项和![]() 。
。
21.(理)已知当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
(文)已知二次函数![]() 的图象经过原点,其导函数为
的图象经过原点,其导函数为![]() 。一次函数
。一次函数![]() ,且不等式
,且不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的解析式。
的解析式。
22.已知椭圆![]() 的方程是
的方程是![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点。
两点。
(Ⅰ)若椭圆的离心率![]() ,直线
,直线![]() 过点
过点![]() ,且
,且![]() ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)直线![]() 过椭圆的右焦点
过椭圆的右焦点![]() ,设向量
,设向量![]() ,若点
,若点![]() 在椭圆
在椭圆![]() 上,求
上,求![]() 的取值范围。
的取值范围。