高三元月数学测试题
一、 选择题:本大题共10题,每小题5分,共50分,在每小题给出的四个选项中,只 有一项是最符合要求的。
1.(理)对于两个非空数集A、B,定义点集如下:A×B={(x,y)︳x∈A,y∈B },若A={1,3},B={2,4},则点集A×B的非空真子集的个数是( )
A、4 B、8 C、14 D、16
(文)集合A={(x,y)∣2x+y=5,x∈N,y∈N},则A的非空真子集的个数为( )
A、4 B、5 C、6 D、7
2.在△ABC中,“A>300”是“sinA>![]() ”的( )
”的( )
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
3.已知函数的反函数满足,则的最小值 为( )
A、4 B、6 C、9 D、2
4.直线y=a与函数f(x)=x3-3x的图象有相异三个交点,则a的取值范围是( )
A、(-2,2) B、[-2,2] C、[-2,3] D、(-1,2)
5、(理)已知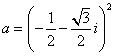 ,则1+a+a2+a3+…+a2006=( )
,则1+a+a2+a3+…+a2006=( )
A、a B、![]() C、1
D、0
C、1
D、0
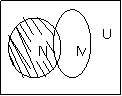 (文)设全集U是实数集R,M{x︴x2>4},N={x︱
(文)设全集U是实数集R,M{x︴x2>4},N={x︱![]() },则图中阴影部分所表示的集合是( )
},则图中阴影部分所表示的集合是( )
A、{x︱-2≤x<1} B、{x∣-2≤x≤2} C、{x∣1<x≤2}
D、{x︱x<2}
6、等差数列{an}中,![]() ,则
,则![]() ( )
( )
A、20 B、22 C、24 D、-8
7、给出下列命题,则其中的真命题是( )
A、若直线m,n都平行于平面![]() ,则m、n一定不是相交直线。
,则m、n一定不是相交直线。
B、已知平面![]() ,直线m⊥n,若
,直线m⊥n,若![]() ,则
,则![]() 。
。
C、直线m、n在平面![]() 内的射影分别是一个点和一条直线,且m⊥n,则
内的射影分别是一个点和一条直线,且m⊥n,则![]() .
.
D、直线mn是异面直线,或![]() ,则n必与
,则n必与![]() 相交。
相交。
8、从2007名学生中选取50名组成参观团,若采用下面的方法选取:先用简单随机抽样从2007名剔除7人,剩下的2000人再按系统抽样的方法进行,则第人入选的概率( )
A、不全相等 B、均不相等 C、都相等,且为![]() D、都相等,且为
D、都相等,且为![]()
9、设F1、F2为椭圆的两个焦点,A为椭圆上的点,且![]() ,
,![]() ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、(理)设f(x-1)=x+x2+…+xn,且f(x)的展开式中所有项的系数的系数和为An,则![]() 的值为( )
的值为( )
A、2 B、![]() C、
C、![]() D、-2
D、-2
(文)若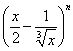 二项展开式中只有第5项的二项式系数最大,则展开式中常数项为( )
二项展开式中只有第5项的二项式系数最大,则展开式中常数项为( )
A、-7 B、7 C、-28 D、28
二、填空题:本大题共5小题,每小题4分(第15小题每空2分),共20分。
11、f(x)=(4a-3)x+b-2a,x∈[0,1],若f(x)≤2恒成立,则a+b的最大值为
12、在映射f:A→B中,若B中的每一个元素都有原象,则称这样的映射为从A到B的满射。若A中有4个元素,B中有3个元素,则从A到B的满射有 个。
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
13、将n2个正整数1,2,3,…,n2填 入n×n方格中,使其每行、每列、每条对角线上的数的和相等,这个正方形叫做n阶幻方。记f(n)为n阶幻方对角线的和,如右图就是一个3阶幻方,可知f(3)=15,是f(5)= 。
14、若f(x)是定义在R上的奇函数,且满足f(x-2)=-f(x),给出下列四个结论:①f(2)=0;②f(x)是以4为周期的周期函数;③f(x)的图象关于直线x=0对称 ;④f(x+2)=f(-x),其中所有正确结论的序号是
15、已知点P(x,y)在椭圆9x2+4y2=36上,则2x+y的最大值为 ;此时点P的坐标为 。
三、解答题:本大题共6小题,共80分。
16.(本小题满分 12分)设函数f(x)=![]() ,其中
,其中![]() ,
,
(Ⅰ)求f(X)的最小正周期;
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,f(A)=2,a=![]() ,b+c=3(b>c),求b、c的长。
,b+c=3(b>c),求b、c的长。
17、(本小题满分12分)(理)在一次购物投资活动中,假设某10张奖券中有一等奖1张,可获价值50元的奖品;二等奖3张,每张可获价值10元的奖品;其余6张没有奖。某顾客从这10张奖券中任抽2张,求
(Ⅰ)该顾客中中奖 的概率;
(Ⅱ)该顾客获得的奖品总价值![]() (元)的概率分布列和期望E
(元)的概率分布列和期望E![]() 。
。
(文)加工某种零件需经过三道工序,设第一、二、三道工序的合格率分别为![]() 且各道工序互不影响。
且各道工序互不影响。
(Ⅰ)求该种零件的合格率;
(Ⅱ)从该种零件中任取3件,求恰好取到一件合格品的概率和至少有一件合格品的概率 。
18、(本小题满分14分)如图所示,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,BD与平面AA1 B1B所成的角为300,AE⊥BD于E,F为A1B1的中点。
(1)求异面直线AE与BF所成的角;(用反三角函数表示);
(2)求平面BDF与平面AA1B所成的二面角(锐角)的大小(用反三角函数表示);
 (3)(理)求点A到平面BDF的距离。
(3)(理)求点A到平面BDF的距离。
19、(本小题满分14分)(理)已知a为实数,函数![]() .
.
(1)若a≥0,证明方程f(X)=0有唯一实根;
(2)若a<0,求函数![]() 的单调区间。
的单调区间。
(文)已知函数f(x)=ax3+bx2-3x在区间![]() 及
及![]() 上为增函数,在[-1,1]上为减函数。
上为增函数,在[-1,1]上为减函数。
(1)求f(x)的表达式;
(2)若f(x)≤m(x∈[-2,1])上恒成立,求m 的最小值 。
20、(本小题满分14分)已知点集L={(x,y)![]() },其中
},其中![]() ,又知点列
,又知点列![]() 为L与y轴的交点。等差数列{an}的公差为1,
为L与y轴的交点。等差数列{an}的公差为1,![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)若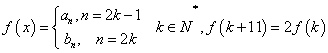 ,求出k的值;
,求出k的值;
(Ⅲ)(理)研究数列{an},{bn},发现数列{bn}有如下性质:设Sn是其 前n项和,则![]() 是一个与n无关的常数,请你进一步研究,对任意一个等差数列{Cn},Tn是其前n和,是否存在一个与n无关的常数k,使
是一个与n无关的常数,请你进一步研究,对任意一个等差数列{Cn},Tn是其前n和,是否存在一个与n无关的常数k,使![]() Tn=kT2n,若存在,求出此常数k,若不存在,请说明理由。
Tn=kT2n,若存在,求出此常数k,若不存在,请说明理由。
(文)对于数列{bn},设Sn是其前n项和,是否存在一个与n无关的常数M,使![]() =M,若存在,求出此常数M,若不存在,请说明理由。
=M,若存在,求出此常数M,若不存在,请说明理由。
21、(本小题满分14分)已知两定点M(-2,0),N(2,0),动点P在轴上的射影是H,如果![]() 和
和![]() 分别是公比为2的等比数列的第三、第四项。
分别是公比为2的等比数列的第三、第四项。
(Ⅰ)求动点P的轨迹方程的C;
(Ⅱ)已知过点N的直线l交曲线C于x轴下文两个不同点A、B,R为AB的中点,若过R与定点Q(0,-2)的直线交x轴于点D(x0,-2),求x0的取值范围。
答 案
一、C(C)、 B、 C、 A、 D(C)、 C、 C、 D、 D、 A(B)
二、11.![]() 12。36个 13.65 14。①②④ 15. 5;
12。36个 13.65 14。①②④ 15. 5;![]()
三、16.解:(1)
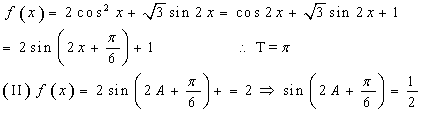
由于A为三角形的内角,![]() ,由余弦定理,有
,由余弦定理,有![]() ,又b+c=3且b>c,所以b=2,c=1.
,又b+c=3且b>c,所以b=2,c=1.
17.解:(理)(Ⅰ)共有10张奖券,能获奖的有4张,故获奖的概率为![]()
(Ⅱ)![]() 的所有可能值为:0;10;20 ;50;60(元)且
的所有可能值为:0;10;20 ;50;60(元)且
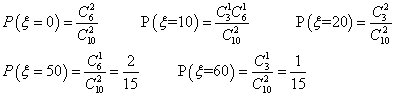 故
故![]() 的分布列为:
的分布列为:
|
| 0 | 10 | 20 | 50 | 60 |
| P | 1/3 | 2/5 | 1/15 | 2/15 | 1/15 |
从而期望E![]() =
=![]()
(文)(Ⅰ)p=![]()
(Ⅱ)由(Ⅰ)可知该种零件的合格率为![]() ,由独立重复实验的概率分布有:恰好取到一件合格品的概率为
,由独立重复实验的概率分布有:恰好取到一件合格品的概率为![]() 至少取到一件合格品的概率为
至少取到一件合格品的概率为![]() 。
。
18.(1)![]() (2)
(2)![]() (3)
(3)![]()
19.(理)(Ⅰ)由![]() 所以函数f(x)的定义域为R。又a≥0,所以
所以函数f(x)的定义域为R。又a≥0,所以![]() 在R上恒成立,故f(x)=0在R上有唯一实根x=0。
在R上恒成立,故f(x)=0在R上有唯一实根x=0。
(Ⅱ)若a<0,![]()
① 若a<-1,![]() 在R上恒成立,故f(x)在R上减函数,即(-∞,+∞)上均为f(x)的递减区间。
在R上恒成立,故f(x)在R上减函数,即(-∞,+∞)上均为f(x)的递减区间。
②
若a=-1,对x≠0,恒有![]() ,故f(x)在(-∞,0)和(0,+∞)上均为减函数,又函数f(x)在x=0处连续,故f(x)的单调区间为R。
,故f(x)在(-∞,0)和(0,+∞)上均为减函数,又函数f(x)在x=0处连续,故f(x)的单调区间为R。
③ 若-1<a<0,则由(*)可知,f(X)在(-∞,![]() )及(-
)及(-![]() ,+∞)上为减函数;在(-
,+∞)上为减函数;在(-![]() ,
,![]() )上为增函数。
)上为增函数。
(文)(Ⅰ)![]() ,依题意
,依题意![]() 解得a=1,b=0,
解得a=1,b=0,![]() .
.
(Ⅱ)![]() 在[-2,1]上f(x)与
在[-2,1]上f(x)与![]() 的变化情况如下表:
的变化情况如下表:
| -2 | (-2,-1) | -1 | (-1,1) | 1 | |
|
| + | 0 | - | 0 | |
| F(x) | -2 | 增 | 极大值2 | 减 | -2 |
由上表可知,f(x)在[-2,1]上的了大值为f(-1)=2。
而f(X)≤m∈(x[-2,1]上恒成立![]()
所以m≥2,故m的最小值为2。
20.(Ⅰ)由题设有L={(x,y)y=2x+1},故L为直线y=2x+1,它与y轴的交战为P1(0,1)又数列{an}是以1为公差的等差数列,所以![]() ,故
,故![]() .
.
(Ⅱ)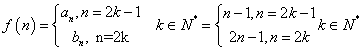
当k为奇数时,![]()
当k为偶数时,![]() .
.
(Ⅲ)(理)对于任意数列{Cn},设其通项公式为![]() ,则
,则![]() .假设存在与n无关常数k,使Tn=kT2n,则
.假设存在与n无关常数k,使Tn=kT2n,则![]() 整理得(4k-1)dn=(2c1-d)(1-2k),要使此式与n无关,则d=0或4k-1=0
整理得(4k-1)dn=(2c1-d)(1-2k),要使此式与n无关,则d=0或4k-1=0
所以①当d=c1=0时,k为任意实数;
②当d=0时,c1≠0时,![]() ;
;
③当d=2c1≠0时,k=![]() .
.
(文)![]() ,假设存在与n无关的常数M,使
,假设存在与n无关的常数M,使![]() ,即
,即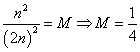 ,故存在与n无关的常数M=1/4,使
,故存在与n无关的常数M=1/4,使![]() .
.
21.解:(Ⅰ)设P(x,y),则H(0,y),
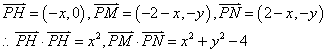
于是:2x2=x2+y2-4(x≠0),故动点P的轨迹方程为:y2-x2=4(x≠0)。
(Ⅱ)设直线l的方程为x=![]() y+2,代入上述方程中,整理得
y+2,代入上述方程中,整理得![]() ,设A(x1,y1),B(x2,y2),则有
,设A(x1,y1),B(x2,y2),则有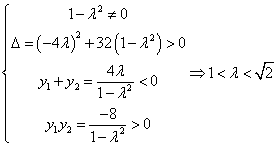
又R的坐标为![]() ,可得直线RQ的方程为
,可得直线RQ的方程为![]() .
.
令y=0得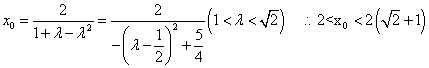 .
.