高三月考数学试题(新课程)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷1至2页。第II卷3至8页。共150分。考试时间120分钟。
第I卷(选择题60分)
注意事项:1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答,不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
一、选择题:本大题共12分,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、若集合M={y y=![]() },P={y y=
},P={y y=![]() }, 则M∩P= ( )
}, 则M∩P= ( )
A.{y 0<y≤![]() } B.{y0≤y≤
} B.{y0≤y≤![]() } C.{y y>0} D.{y y≥0}
} C.{y y>0} D.{y y≥0}
2、下列四个集合中,是空集的是 ( )
A .![]() B .
B .![]()
C. {![]() D .
D .![]()
3、设函数f(x)=![]() , 当x∈[-4, 0]时, 恒有f(x)≤g(x), 则a可能取的一个值是(
)
A. -5
B. 5 C. -
, 当x∈[-4, 0]时, 恒有f(x)≤g(x), 则a可能取的一个值是(
)
A. -5
B. 5 C. -![]() D.
D. ![]()
4、下列四组函数中,表示同一函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5、已知 函数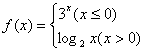 ,那么
,那么![]() 的值为(
)
的值为(
)
A. 9 B.![]() C.
C.![]() D.
D.![]()
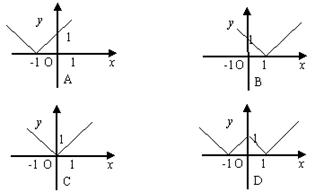 6、
6、![]() ( )
( )
7、若函数![]() 在R上为增函数,则a的取值范围是( )
在R上为增函数,则a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、![]() 、
、![]() 为锐角a=sin(
为锐角a=sin(![]() ),b=
),b=![]() ,则a、b之间关系为( )
,则a、b之间关系为( )
A.a>b B.b>a C.a=b D.不确定
9、将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到
个单位,得到![]() 的图象,则
的图象,则![]() 等于(
)
等于(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、若函数![]() 的图象与x轴有公共点,则m的取值范围是( )
的图象与x轴有公共点,则m的取值范围是( )
A.m≤-1 B.-1≤m<0 C.m≥1 D.0<m≤1
11、使![]() (ω>0)在区间[0,1]至少出现2次最大值,则ω有( )
(ω>0)在区间[0,1]至少出现2次最大值,则ω有( )
A.最小值![]() B.最大值
B.最大值![]() C.最小值4π D.最大值4π
C.最小值4π D.最大值4π
12、函数y=logax在![]() 上总有y>1,则a的取值范围是( )
上总有y>1,则a的取值范围是( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C. ![]() D.
D.![]() 或
或![]()
第II卷(非选择题共90分)
注意事项:
1.第II卷共4页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、填空题:(本大题共4小题,每小题4分,共16分。把答案填在题中横线上。)
13.把函数y = cos(x+![]() )的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_________。
)的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_________。
14.定义在(-∞,+∞)上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0)上是增函数,下面关于f(x)的判断:
①f(x)是周期函数; ②f(x)的图象关于x=1对称;
③f(x)在[0,1]上是增函数 ④f(x)在[1,2]上为增函数 ⑤f(2)=f(0)
其中正确的判断是 .(把你认为正确的判断都填上)
15.若函数![]() 是偶函数,则
是偶函数,则![]() ,
,![]() (a∈R)的大小关系是
(a∈R)的大小关系是![]()
![]() .
.
16.若![]() ,则函数
,则函数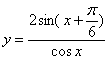 的值域是 。
的值域是 。
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)已知函数![]()
(1)判断函数的单调性,并用定义证明; (2)求函数的最大值和最小值.
(18)(本小题满分12分)若函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,求函数
,求函数![]() 的单调区间和周期。
的单调区间和周期。
(19)(本小题满分12分)设函数f(x)对任意x、y∈R,都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0.
(1)证明:f(x)为奇函数; (2)证明:f(x)在R上为减函数.
(20)(本小题满分12分)已知函数![]()
(I)求函数![]() 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(II)函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
(21)(本小题满分12分)某租赁公司拥有汽车100辆,当每辆汽车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车辆会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
(22)(本小题满分14分)设函数![]() .
.
(1)在区间![]() 上画出函数
上画出函数![]() 的图像;
的图像;
(2)设集合![]() . 试判断集合
. 试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.
高三月考数学试题(新课程)答案
一、选择题: CDADB BABCB AB
二、填空题:13、![]() 14、①②④⑤ 15、≥ 16、[1+
14、①②④⑤ 15、≥ 16、[1+![]() ,4]
,4]
三、17、(1)解:![]() 在[3,5]上为增函数。证明如下:……………………………………2分
在[3,5]上为增函数。证明如下:……………………………………2分
设![]() 是区间[3,5]上的任意两个实数且
是区间[3,5]上的任意两个实数且![]() ,则
,则
![]() …………………4分
…………………4分
∵3≤![]() <
<![]() ≤5 ∴
≤5 ∴![]() <0,
<0,![]() <0
<0 ![]() <0
<0
∴![]() <0 即
<0 即![]()
∴![]() 在[3,5]上为增函数…………………………………………………8分
在[3,5]上为增函数…………………………………………………8分
(2)由(1) ![]() 在[3,5]上为增函数,所以
在[3,5]上为增函数,所以
![]() 在[3,5]上有最大值
在[3,5]上有最大值![]() =-2,有最小值
=-2,有最小值![]() =-4………………12分
=-4………………12分
18、解:由已知得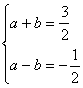 或
或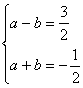 …………………………………………2分
…………………………………………2分
解得![]() 或
或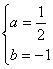 ………………………………………………………………6分
………………………………………………………………6分
当![]() 时
时 ![]() 周期为2π
周期为2π
单调减区间为[2kπ-![]() ,2kπ+
,2kπ+![]() ],k∈Z;
],k∈Z;
单调增区间为[2kπ+![]() ,2kπ+
,2kπ+![]() ],k∈Z…………………………………9分
],k∈Z…………………………………9分
当![]() 时
时 ![]() 周期为2π
周期为2π
单调增区间为[2kπ-![]() ,2kπ+
,2kπ+![]() ],k∈Z;
],k∈Z;
单调减区间为[2kπ+![]() ,2kπ+
,2kπ+![]() ],k∈Z…………………………………12分
],k∈Z…………………………………12分
19、证明:(1)由已知f(x+y)=f(x)+f(y) 令x=y=0得 f(0)=0……………2分
令y=-x,得f(x-x)=f(x)+f(-x)
∴f(x)+f(-x)=0 ∴f(x)为奇函数。……………………………5分
(2)设![]() 是 (-∞,+∞)上的任意两个实数,且
是 (-∞,+∞)上的任意两个实数,且![]()
∵![]() >0,
>0,![]() <0…………………………………8分
<0…………………………………8分
由(1)知f(x)为奇函数
∴![]() =
=![]() +
+![]() =
=![]() -
-![]() <0
<0
∴![]() <
<![]() ∴ f(x)在R上为减函数……………………12分
∴ f(x)在R上为减函数……………………12分
20、解:(I)![]()
![]()
![]() ………………4分
………………4分
![]() 的最小正周期
的最小正周期![]() ………………………………………………6分
………………………………………………6分
由题意得![]()
即 ![]()
![]() 的单调增区间为
的单调增区间为![]() ………………………………8分
………………………………8分
(II)方法一:先把![]() 图象上所有点向左平移
图象上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象,再把所得图象上所有的点向上平移
的图象,再把所得图象上所有的点向上平移![]() 个单位长度,就得到
个单位长度,就得到![]() 的图象。
的图象。
方法二:把![]() 图象上所有的点按向量
图象上所有的点按向量![]() 平移,就得到
平移,就得到![]() 的图象。…………………………………………………12分
的图象。…………………………………………………12分
21、解:(1)∵3600-3000=600元 100-![]() =88 ∴能租出88辆车……………4分
=88 ∴能租出88辆车……………4分
(2)设每辆车的月租金定为x元时,租赁公司的月收益为y元.
![]()
=![]() ……………………………………………………8分
……………………………………………………8分
∴x=4050元时,函数有最大值307050元
∴当每辆车的月租金定为4050元时,租赁公司的月收益最大为307050元……12分
22、[解](1)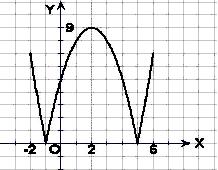 ………………………………4分
………………………………4分
(2)方程![]() 的解分别是
的解分别是![]() 和
和![]() ,由于
,由于![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增,因此
上单调递增,因此
![]() .
…………………………6分
.
…………………………6分
由于![]() ∴B
∴B![]() A. ………………………………8分
A. ………………………………8分
(3)[解法一] 当![]() 时,
时,![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() . 又
. 又![]() ,……………………10分
,……………………10分
①
当![]() ,即
,即![]() 时,取
时,取![]() ,
,
![]()
![]() .
.
![]() ,
,
则![]() . …………………………………………………………12分
. …………………………………………………………12分
②
当![]() ,即
,即![]() 时,取
时,取![]() ,
, ![]() =
=![]() .
.
由
①、②可知,当![]() 时,
时,![]() ,
,![]() .
.
因此,在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.…………14分
图像的上方.…………14分
[解法二] 当![]() 时,
时,![]() .
.
由![]() 得
得![]() ,
,
令 ![]() ,解得
,解得 ![]() 或
或![]() ,……………………………10分
,……………………………10分
在区间![]() 上,当
上,当![]() 时,
时,![]() 的图像与函数
的图像与函数![]() 的图像只交于一点
的图像只交于一点![]() ; 当
; 当![]() 时,
时,![]() 的图像与函数
的图像与函数![]() 的图像没有交点.
的图像没有交点.
如图可知,由于直线![]() 过点
过点![]() ,当
,当![]() 时,直线
时,直线![]() 是由直线
是由直线![]() 绕点
绕点![]() 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方. …………………………………………………………………14分
图像的上方. …………………………………………………………………14分