高三月考数学试题
第Ⅰ卷（选择题 共60分）
一、选择题：共12小题每小题5分，满分60分，在每小题给出的四个选项中，只有一个选项是符合题目要求的，把正确的选项的代号涂在答题卡上.
1. 已知映射
，其中A=B=R，对应法则
，对于实数
在集合A中不存在原象，则k的值范围: （ ）
A．k>1 B．k≥1 C．k<1 D．k≤1
2. 已知
则
等于 （ ）
A．
B．
C．
D．
3. 函数
零点所在的区间是 （ ）
A．
B．
C． 
D．
4. 设x，y，z是空间不同的直线或平面，对于下列四种情形，使“x⊥z且y⊥z
x//y”为真命题的是: （ ）
①x，y，z均为直线； ②x，y是直线，z是平面
③z是直线，x，y是平面； ④x，y，z均为平面.
A．①，② B．①，③ C．③，④ D．②，③
5. 已知点M（4，2）与N（2，4）关于直线l对称，则直线l的方程为（ ）
A．
B．
C．
D．
|
|
的大致图象是： （ ）
A B C D
7. 一个等差数列{an}中，a1 = －5，它的前11项的平均值是5，若从中抽取一项，
余下项的平均值是4，则抽取的项是 （ ）
A．a9 B．a8 C．a11 D．a10
8. 若函数
对任意
都有
，则
（ ）
A．0 B．－2 C．2 D．－2或2
9. 若直线
的周长，则
的最小值是 （ ）
A．4 B．3 C．
D．－3
10. 当0<x<
时，函数f（x）＝
的最小值是 （ ）
A．1 B．2 C．4 D．8
11. 若函数
在区间
内单调递增，则
的取值范围是 （
）
A．
B． 
C．
D．
12.设函数
，对任意实数t都有
成立，则函数值
中，最小的一个不可能是 （ ）
A．
B．
C．
D．
二、填空题：本大题有4个小题，每小题4分，共16分；将答案填写在答卷相应的题号后面的空格内.
13.一个正三棱子柱的三视图如下所示，则它的表面积为： 。
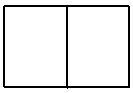
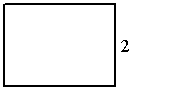
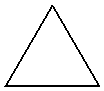
正视图 左视图 俯视图
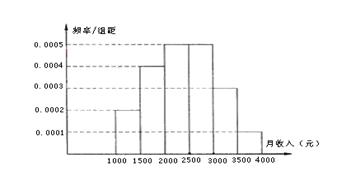
14．一个社会调查机构就某地居民的月收入调查10 000人，并根据所得数据画了样本的频率分布直方图（如下图）。为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在（2 500，3 000）（元）月收入段应抽出
人。
|
15已知
，点C在∠AOB内，且∠AOC=45°，设
，则
等于
.
|
|
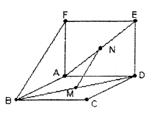
①MN⊥AD；
②MN与BF的是对异面直线；
③MN//平面ABF
④MN与AB的所成角为60°
三、解答题：本大题共6个小题，满分74分，解答时要求写出必要的文字说明、证明过程或演算步骤.
17. 已知集合
（1）当m=3时，求
；
（2）若
求实数m的值.
18. A、B、C为△ABC的三内角，且其对边分别为a、b、c.若
,
，且
.
（1）求角A的大小；
（2）若a＝2，三角形面积S＝，求b+c的值.
19. 已知函数
、
对任意实数x、y分别满足
①
②
为正整数
（1）求数列
、
的通项公式；
（2）设
的前n项和。
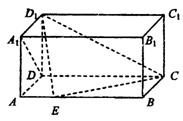
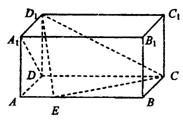
20．如图，在长方体ABCD—A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动.
|
（2）AE等于何值时，二面角D1—EC—D的大小为
21.某地西红柿从2月1日起开始上市，通过市场调查，得到西红柿种植成本Q（单位：元/102kg）与上市时间t（单位：天）的数据如下：
| 时间/t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
（1）根据上表数据，从下列函数中选取一个函数模型描述西红柿种植成本Q与上市时间t的变化关系：
，并说明选取的理由；
（2）利用您选取的函数模型，求西红柿种植成本最低时的上市天数及最低种植成本.
22.设二次函数f(x)=ax2+bx+c,(a,b,c∈R)满足下列条件：
①当x∈R时，f(x)的最小值为0，且f(x-1)=f(-x-1)成立；
②当x∈(0,5)时，x≤f(x)≤2
+1恒成立。
（1）求f(1)的值；
（2）求f(x)的解析式；
（3）求最大的实数m(m>1),使得存在实数t,只要当x∈
时，就有f(x+t)≤x成立。
高三月考数学参考答案
一．选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | B | D | D | A | C | D | A | D | C | B |
二．填空题
13．24+
14.25 15.
16.①③
三．解答题
17解：
|
|
=
（2）
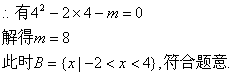
18解析:（1）∵，，且
·
＝，
∴－cos2＋sin2＝， 即－cosA＝，又A∈(0，k
)，
∴A＝
（2）S△ABC＝bc·sinA＝b·c·sin＝
，∴bc＝4,
又由余弦定理得：a2=b2+c2－2bc·cos120°＝b2+c2+bc ,
∴16＝(b+c)2，故b+c＝4.
19.（1）
成等比数列，
由②中令
成等差数列，
（2）
20．解法一：（1）
（2）过D作DH⊥CE于H，连D1H、DE，
则过D1H⊥DE
解法二：以D为坐标原点，直线DA、DC、DD1分别为x、y、z轴，建立空间直角坐标系，设AE=x，则A1（1,0,1）、D1（0,0,1）、E（1,x,0）、A（1,0,0）、C（0,2,0）
（1）
（2）设平面D1EC的法向量为n=（a,b,c）
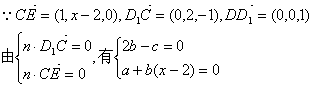
21.解：（1）由表格数据可知，随着时间t的增大，种植成本Q先减后增；而这些函数中除了Q = at2 + bt + c之外的三个函数都是单调函数，因而均不适合描述西红柿种植成本与上市时间之间的变化关系。应当选择Q = at2 + bt + c作为描述西红柿种植成本Q与上市时间t变化关系的函数模型。 …………………………………………………4分
（2）
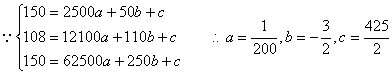
…………………………………………10分
∴由二次函数性质可知，当t = 150（天）时，西红柿的种植成本最低，此时的最低种植成本Q = 100（元/102kg） …………………………………………………… 12分
22(1)在(2)中令x=1,有1≤f(1)≤1,故f(1)=1
(2)由(1)知二次函数的关于直线x=-1对称,且开口向上
故设此二次函数为f(x)=a(x+1)2,(a>0),∵f(1)=1,∴a=
∴f(x)= (x+1)2
理科(3)假设存在t∈R,只需x∈[1,m],就有f(x+t)≤x.
f(x+t)≤x
(x+t+1)2≤xx2+(2t-2)x+t2+2t+1≤0.
令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m].
∴m≤1-t+2
≤1-(-4)+2
=9
t=-4时,对任意的x∈[1,9]
恒有g(x)≤0, ∴m的最大值为9.
文科:(3)f(x+t)≤x x2+(2t-2)x+t2+2t+1≤0
令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,3].
∴-4≤t≤-4+2
∴tmax=-4+2
（本题满分12分）
（本题满分12分）
（本题满分12分）
（本题满分12分）