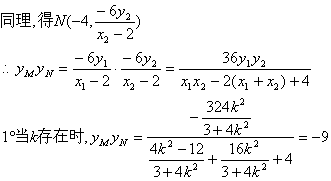高三综合测试（三）数学（理）试题
本试卷选择题和非选择题两部分，满分150分。考试用时120分钟。
注意事项：
1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡上，用2B铅笔将试卷类型（A）填涂在答题卡上。
2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑：如需改
动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区
域内的相应位置上；如需改动，先划掉原来的答案，然后写上新的答案；不准使用
铅笔和涂改液。不按以上要求作答的答案无效。
4．考生必须保持答题卡整洁，考试结束后，将本试题卷和答题卡一并交回。
第一部分 选择题（共40分）
一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知命题
是 （ ）
A．
B．
C．
D．
2．已知等差数列
的公差为2，若
成等比数列，则
的值为 （ ）
A．－4 B．－6 C．－8 D．－10
3．已知
的值为 （ ）
A．
B．
C．
D．
4．已知向量
，则
（ ）
A．
B．
C．
D．
5．在极坐标系中，曲线
所围成的图形的面积是 （ ）
A．
B．
C．
D．
6．已知地球半径为R，A地在北纬45°东经120°，B地在南纬75°东经120°，则A、B
的球面距离为 （ ）
A．
B．
C．
D．
7．若函数
外的切线的倾斜角为 （ ）
A．90° B．0° C．锐角 D．钝角
8．对一切实数x，不等式
恒成立，则实数a的取值范围是 （ ）
A．
B．
C．
D．
第二部分 非选择题（共110分）
二、填空题：本大题共6小题，每小题5分，共30分
9．由曲线
所围成的图形面积是
.
10．如果函数
对称，那么a=
.
11．已知点P是圆
上任意一点，P点关于直线
的对称点也在圆C上，则实数a=
.
12．编辑一个运算程序：1＆1=2，若1＆n=k，则1＆（n+1）=k+3，则1＆2006的输出结果为 .
13．若x、y满足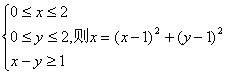
的取值范围是
.
|
|
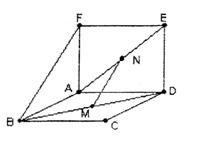
①MN⊥AD；
②MN与BF的是对异面直线；
③MN//平面ABF
④MN与AB的所成角为60°
三、解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.
|
（1）当m=3时，求
；
（2）若
求实数m的值.
16．（本小题满分12分）已知
是等差数列，其前n项和为
（1）求数列的通项公式；
（2）设
是等比数列，并求其前n项和Tn
17．（本小题满分14分）在△ABC中，A、B、C的对边分别是a、b、c，已知
（1）试判断△ABC的形状；
|
，求角B的大小.
|
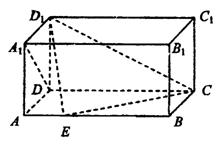
18．（本小题满分14分）如图，在长方体ABCD—A1B1C1D1中，AD—AA1—A，AB=2，点E在棱AB上移动.
（1）证明：D1E⊥A1D
（2）AE等于何值时，二面角D1—EC—D的大小为
19．（本小题满分14分）已知函数
的图像与函数
的图象相切，记
（1）求实数b的值及函数F（x）的极值；
（2）若关于x的方程F（x）=k恰有三个不等的实数根，求实数k的取值范围.
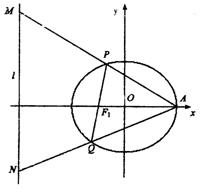
20．（本题满分14分）已知椭圆
为其左焦点，A为右顶点，l为左准线，过F1的直线l′与椭圆交于异于A的P、Q两点.
（1）求
的取值范围；
|
求证：M、N两点的纵坐标之积为定值－9
参考答案
一、DBAA DDCB
二、
9．e－2
10．－1
11．－6
12．6017
13．
14．① ③
三、解答题
15．解：
|
|
=
（2）
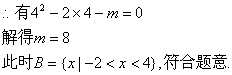
16．解：
（1）
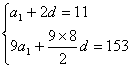
（2）
17．解：
（1）由余弦定理得：
（2）
中
①
②
②÷①得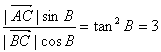
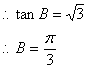
另解：（2）
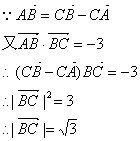
同理
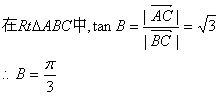
18．解法一：（1）
（2）过D作DH⊥CE于H，连D1H、DE，
则过D1H⊥DE
解法二：以D为坐标原点，直线DA、DC、DD1分别为x、y、z轴，建立空间直角坐标系，设AE=x，则A1（1,0,1）、D1（0,0,1）、E（1,x,0）、A（1,0,0）、C（0,2,0）
（1）
（2）设平面D1EC的法向量为n=（a,b,c）
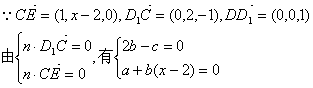
19．解：（1）依题意，令
，得
列表如下：
|
|
|
|
| －1 |
|
|
| + | 0 | － | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值0 | ↗ |
从上表可知
处取得极小值.
（2）由（1）可知涵数
作函数
的图象，当
的图象与函数的图象有三个交点时，关于x的方程
|
20．解：
（1）当直线PQ的斜率不存在时，PQ方程为
得
（2）AP的方程为
