高三数学期末测试

　　 高三数学期末测试　　　　　 姓名　　　　　 　

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分.考试时间120分钟.

第Ⅰ卷（选择题 共40分）

注意事项：

1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。不能答在试卷上。

　　3．考试结束，监考人将本试卷和答题卡一并收回.

一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集ｕ=R，集合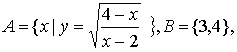　则Ａ∩（Ｃ_ｕＢ）＝（　　）

　　A．（2，3）∪（3，4）　　　　　　　　B．（2，4）

　　C．（2，3）∪（3，4　　　　　　　　 D．（2，4

2．过点引直线，使它与两点、距离相等，则此直线方程为（　）

　　或　　　　

　　或　　　　

3．已知数列{a_n}是等差数列，且a₃+a₁₁=50，a₄=13，则a₂等于　　　　　　　　　 （　　）

　　A．1　　　　　　　B．4　　　　　　　C．5　　　　　　　D．6

4．已知双曲线的焦点为、，点在双曲线上且轴，则到直线的距离为(　　   )

A． 　　　　　　　　　B． 　　　　　　　　　C． 　　　　　　　　　　　D．

5．下列命题：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

⑴ 若“p或q”是假命题，则“”是真命题；

⑵ 或；

⑶ 命题“都是偶数，则是偶数”的逆否命题是“若不是偶数，则都不是偶数”；

⑷ 是不等式与不等式解集相同的充要条件．其中真命题的是　　　　 （　　）

A．⑴　　　　　　　B．⑴⑵⑷　　　　 C．⑴⑷　　　　　 D．⑶⑷

6．的值为（　　　　  ）

A．　　　 B．　　 Ｃ．　　  Ｄ．

７．一种计算装置，有一个数据入口和一个运算出口，按照某种运算程序：（ⅰ）当从口输入自然数1时，从口得到；（ⅱ）当从口输入自然数时，在口得到的结果是前一结果的倍.则当从口输入自然数4时，从口得到的数为 （　　）

A．　　　　　　　 　B．　　　　　　 C．　　　　　　　 D．　　　　　　　

８．给出如下4个命题：①对于任意一条直线a，平面α内必有无数条直线与a垂直；②若α、β是两个不重合的平面，l、m是两条不重合的直线，则α//β的一个充分而不必要条件是l⊥α，m⊥β，且l//m；③已知a、b、c、d是四条不重合的直线，如果a⊥c，a⊥d,b⊥c,b⊥d，则 “a//b” 与 “c//d” 不可能都不成立；④已知命题P：若四点不共面，那么这四点中任何三点都不共线.则命题P的逆否命题是假命题。

 以上命题中，正确命题的个数（　　）　　　　

A．1　　B．2　　　　　 C．3 　　　　D．4

第Ⅱ卷（非选择题，共110分）

二、填空题：本大题共6小题，每小题5分，共30分.请把答案填写在题中横线上.

9．设动点P的坐标为（，向量a=（x，0），b=（1，y），（a+ b）⊥（a－ b）.

　 则点P的轨迹方程为­­­­­­­­­­­­______________________

10．(x² +3x+2)⁵ 二项展开式中x²项的系数是______

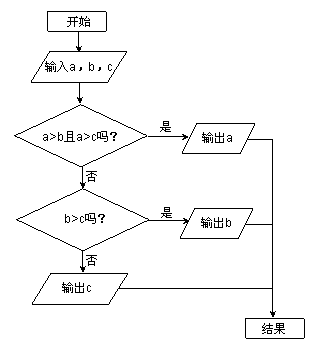11．右图所示的流程图是将一系列指令和问题用框图的形式排列而成，箭头说明下一步是到哪一个框图。阅读这个流程图，回答下列问题：

　　若a<b<c，则输出的数是　　 ；（2分）

　　若a=,b=,c=，则输出的数是　　　　  ．（用字母a、b、c填空）（3分）

 12．若球O的半径长为13，圆O₁为它的一个截面，且OO₁=12，则圆O₁的半径长为　

点A、B为圆O₁上的两定点，AB=10，若C为圆O₁上的动点，则△ABC的最大面积为　

13．有下列四个命题：

①函数的值域是；　

　　②平面内的动点P到点F和到直线:的距离相等，则P的轨迹是抛物线；

　　③直线AB与平面相交于点B，且AB与内相交于C的三条互不重合的直线CD、CE、CF所成的角相等，则AB；

　　④函数的最小正周期是．

　　其中正确的命题的编号是　　　　  ．

14．（三题中选做二题）

　①椭圆的内接矩形的最大面积是　　　　　　 　

②已知x、y、z∈R⁺，且x+y+z=1，则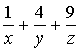的最小值是　　　 　 

③已知圆锥面S，其母线与轴线的夹角为30⁰，又有一平面与圆锥面的轴线成60⁰角并相交于点C，且SC=4，一球与圆锥面相切并在平面的上方与平面相切，则此内切球的半径为　　　　　 　　

三．解答题：

15．（本小题满分13分）

已知 ，。

（Ⅰ）求的值；

（Ⅱ）求的值。

16．（本小题满分13分）

从分别写有的九张卡片中，任意抽取两张，计算：

（Ⅰ）卡片上的数字都是奇数的概率；

（Ⅱ）当两张卡片上的数字之和能被3整除时，就说这次试验成功，求在15次试验中

成功次数的数学期望。

17．　　　　　　  （本小题满分13分）

如图所示，在直三棱柱中，，为棱的中点，且

。

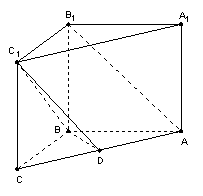
　　（Ⅰ）求证：平面；

（Ⅱ）求异面直线与所成的角；

（Ⅲ）求点到平面的距离。

18．（本题满分13分）

已知数列{a_n}中.

　　（1）求证数列{b_n}是等差数列

　　（2）求数列{a_n}中的最大项与最小项，并说明理由；

　

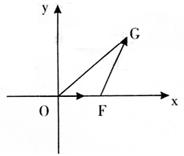
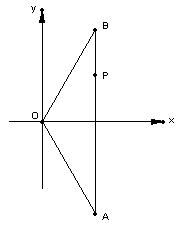
 19．（本题满分14分）以O为原点，所在直线为x轴，建立如图所示的直角坐标系，设·=1，点F的坐标为（t,0），，点G的坐标为（x₀，y₀）.

（1）求x₀关于t的函数x₀=f(t)的表达式，

判断函数f(t)的单调性，并证明你的

判断；

（2）设△OFG的面积，若以O

为中心， Ｆ为焦点的椭圆经过点Ｇ，

求当取最小值时椭圆的方程.

20．如图，在中，，点分线段所成的比，以、所在

直线为渐近线的双曲线恰好经过点，且离心率为．

（Ⅰ）求双曲线的标准方程；

（Ⅱ）若直线（，）与双曲线交于不同的两点、，且、

两点都在以为圆心的同一圆上，求实数的取值范围．

高三数学期末测试参考答案：

一．AC C　 CAC　　BC

二．9. 　10. 800　11、c  b 　12、5 　25 　13、③④

14、①40　②36　③

15．解：（Ⅰ）；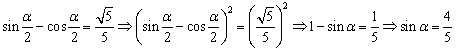

（Ⅱ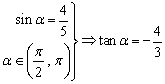），由此及得

．

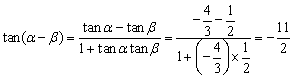16．　　　　　　  （Ⅰ）；

（Ⅱ）一次试验成功的概率为，从而，故

。

17．（Ⅰ）略；　　　 （Ⅱ）；　　（Ⅲ）。

18．解：（1）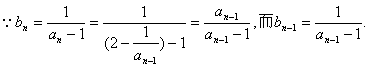

∴{b_n}是首项为，公差d=1的等差数列

　 （2）由（1）得

　　　　设函数

　　　　∴在区间内f(x)为减函数

　　　　∴当x≤3时，f(x)≥f(3)=－1

　　　　  当x≥4时，f(x)≤f(4)=3,

　　　　∴a_n的最小值为a₃=－1，最大值为a₄=3.

另解：a_n=1+.

　　当n≤3时，=a₁>a₂>a₃=－1, 当n≥4时，3=a₄>a₅>a₆>…>a_n>1.

　　∴a_n的最小值为a₃=－1，最大值为a₄=3.

19．解：（1）由题意知：…2分

解得

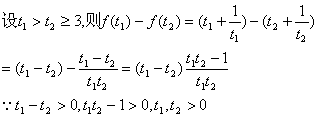
函数f(t)在区间[3，+∞]上单调递增

　 （2）由∴点G的坐标为

∵函数f(t)在区间上单调递增

∴当t=3时，取得最小值，此时点F、G的坐标分别为（3，0）、

由题意设椭圆方程为

由点G在椭圆上，得

∴所求椭圆方程为

20．解：（Ⅰ）因为双曲线的离心率为，所以可设双曲线的方程为，

由此可得渐近线的斜率，从而，．

又因为点分线段所成的比为，故，代入双曲线方程得，故双曲线的方程为；

（Ⅱ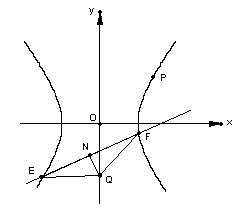）如图所示，由方程组

，

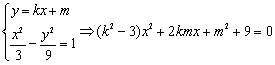　　设、，线段的中

点为，则有

．　　　　　　　……①

由韦达定理得，．因为、两点都在以为圆心的同一圆上，所以，即

．　　　 ……②

由①、②得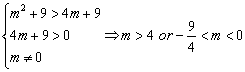．