高三数学期末测试B
一．选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.设全集U=R，
B）是 （ ）
A．
B．
或
C．
D．
2．若函数f(x)同时具有以下两个性质：①f(x)是偶函数，②对任意实数x，都有f(
)= f(
)，则f(x)的解析式可以是
（ ）
A．f(x)=cosx B．f(x)=cos(2x
) C．f(x)=sin(4x) D．f(x) =cos6x
3．已知等比数列
中，
为方程
的两根，则
的值为
A．32 B．64 C．256 D．±64 （ ）
4.对于直线m，n和平面
，
，⊥的一个充分条件是
( )
A．m⊥n，m∥，n∥ B．m⊥n，∩=m，n
C．m∥n，n⊥，m D．m∥n，m⊥，n⊥
5．椭圆的焦点为F1、 F2，过点F1作直线与椭圆相交, 被椭圆截得的最短的线段MN长为
，
的周长为20, 则椭圆的离心率为
（ ）
A． 
B． 
C． 
D． 
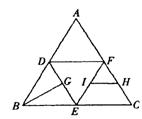
6．如图，在正三角形ABC中，D、E、F分别为各边的中点，G、H、I分别为DE、FC、EF的中点，将△ABC沿DE、EF、DF折成三棱锥以后，BG与IH所成的角的弧度数为
A．
B．
C．
D．
7.将函数 y = cos x－sin x 的图象向左平移 m（m > 0）个单位，所得到的图象关于 y 轴对称，则
m 的最小正值是
（ ）
A. B. C. D.
8.下列同时满足条件：
（1）是奇函数（2）在
上是增函数（3）在上最小值为0的函数是 （ ）
A．
B.
C.
D.
9 过圆
+
－4x=0外一点P(m,n)作圆的两条切线，当这两条切线互相垂直时，m,n 应满足的关系式为（ ）
A. 
+ 
=4
B. 
+=4
C. + =8
D. +=8
10．常州某中学的研究性学习小组为考察天目湖地区的一个小岛的湿地开发情况，从某码头乘汽艇出发，沿直线方向匀速开往该岛，靠近岛时，绕小岛环行两周后，把汽艇停靠岸边上岸考察，然后又乘汽艇沿原航线匀速返回。设t为出发后的某一时刻，S为汽艇与码头在时刻t的距离，下列图象中能大致表示S＝f(x)的函数关系的为
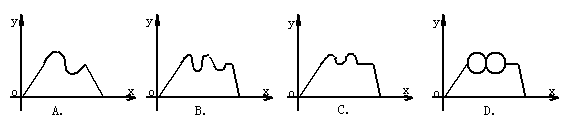
二.填空题：本大题共有6小题，每小题5分，共30分.把答案填在题中横线上.
11．函数
的最小值是
．
12．已知椭圆
与双曲线
具有相同的焦点F1，F2，设两曲线的一个交点为Q,∠QF1F2＝90°，则双曲线的离心率为
．
13．函数
在区间（1，+∞）上是单调增函数，则a的取值范围是
．
14．不等式x >
的解集是
．
15．Sn为等差数列{an}的前n项和，若
，则
=
．
16. 过抛物线y2=2px（p>0）的焦点的直线x－my+m=0与抛物线交于A、B两点，且△OAB（O为坐标原点）的面积为2
，则m6+m4=
三、解答题：本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）设
，
是平面内两个向量
⑴
若
且
，求
；
⑵
若
，求
．
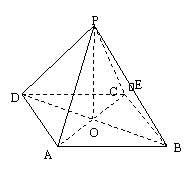18．（本小题满分14分）如图所示,正四棱锥
中，侧棱
与底面
所成的角的正切值为
.
（1）求侧面
与底面所成的二面角的大小；
（2）若
是
的中点，求异面直线
与
所成角的正切值；
（3）问在棱AD上是否存在一点
，使
⊥侧面
，若存在，试确定点的位置；若不存在，说明理由．
19．（本小题满分14分）
已知两个函数
，
.
（Ⅰ）若对任意
[－3，3]，都有
≤
成立，求实数
的取值范围；
（Ⅱ）若对任意
[－3，3]，
[－3，3]，都有
≤
成立，求实数的取值范围。
20.（本小题满分15分）
已知数列
的前
项和
满足
（Ⅰ）求k的值；
（Ⅱ）求；
（Ⅲ）是否存在正整数
使
成立？若存在求出这样的正整数；若不存在，说明理由
21．（本小题满分15分）
在平面直角坐标系中，
为坐标原点，已知两点
、
，若点
满足
（
），点的轨迹与抛物线：
交于
、
两点.
（Ⅰ）求证：
⊥
；
（Ⅱ）在
轴上是否存在一点
，使得过点
直线交抛物线于D、E两点，并以该弦DE为直径的圆都过原点。若存在，请求出
的值及圆心的轨迹方程；若不存在，请说明理由.