高三数学期末考试模拟试题
试题(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分![]() ,共150分
,共150分![]() 测试时间120分钟
测试时间120分钟![]()
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题![]() 每小题5分;共60分
每小题5分;共60分![]() 在每小题给出的四个选项中,只有一项是符合题目要求的
在每小题给出的四个选项中,只有一项是符合题目要求的![]()
1、1、设集合![]() 则下列关系中正确的是( )
则下列关系中正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、已知正方体外接球的体积是![]() ,那么正方体的棱长等于( )
,那么正方体的棱长等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、已知![]() 、
、![]() 是不重合的直线,
是不重合的直线,![]() 、
、![]() 是不重合的平面,则下列命题是真命题的是:( )
是不重合的平面,则下列命题是真命题的是:( )
①若![]() ②
②![]()
③![]() ④
④![]()
A、①③ B、②③ C、③④ D、④
4、当![]() 时,不等式
时,不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、函数![]() 满足
满足![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A、![]() B、
B、![]()
C、![]() D、大小关系随x的不同而不同
D、大小关系随x的不同而不同
6、在等差数列![]() 中,
中,![]() 则前n项和
则前n项和![]() 的最小值为( )
的最小值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、把函数![]() 的图象向右平移
的图象向右平移![]() 个单位,所得图象对应的函数是( )
个单位,所得图象对应的函数是( )
A、非奇非偶函数 B、既是奇函数又是偶函数
C、奇函数 D、偶函数
8、给出下列4个命题:
①若sin2A=sin2B,则△ABC是等腰三角形;
②若sinA=cosB,则△ABC是直角三角形;
③若cosAcosBcosC<0,则△ABC是钝角三角形;
④若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC是等边三角形.
其中正确的命题是( )
A、①③ B、③④ C、①④ D、②③
9、过点![]() 的直线l将圆
的直线l将圆![]() 分成两段弧,当其中的劣弧最短时,直线l的方程是( )
分成两段弧,当其中的劣弧最短时,直线l的方程是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、定义在(![]() ,0)
,0)![]() (0,
(0,![]() )上的奇函数
)上的奇函数![]() ,在(0,
,在(0,![]() )上为增函数,当x>0时,
)上为增函数,当x>0时,![]() 图像如图所示,则不等式
图像如图所示,则不等式![]() 的解集为( )
的解集为( )
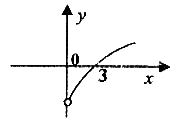
A、![]() C、
C、![]()
B、![]() D、
D、![]()
11、设椭圆的两个焦点为F1,F2,过F2作椭圆长轴的垂线交椭圆于点P,若![]() 为等腰直角三角形,则椭圆的离心率为( )
为等腰直角三角形,则椭圆的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入a元定期储蓄,若年利率为p且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将所有的存款及利息全部取回,(2008年不再存)则可取回的钱的总数(元)为(不计利息税)( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
二、填空题:本大题共4个小题![]() 每小题4分;共16分,把答案填在题中横线上
每小题4分;共16分,把答案填在题中横线上![]()
13、平面内满足不等式组1≤x+y≤3,—1≤x—y≤1,x≥0,y≥0的所有点中,使目标函数z=5x+4y取得最大值的点的坐标是_______________。
14、若A(6,m)是抛物线![]() 上的点,F是抛物线的焦点,且AF=10,则此抛物线的焦点到准线的距离为
。
上的点,F是抛物线的焦点,且AF=10,则此抛物线的焦点到准线的距离为
。
15、图中阴影部分的面积为__________。
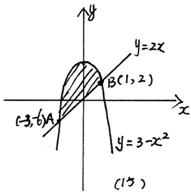
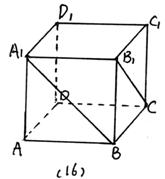
16、在正方体ABCD—A1B1C1D1中直线BA1与B1C所成角的大小为_____________。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤![]()
17、(本小题满分12分)
已知![]() 、
、![]() 、
、![]() 三点的坐标分别为
三点的坐标分别为![]() 、
、![]() 、
、![]() ,
,![]() ,
,
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值。
的值。
18、 (12分) 已知圆C:![]() ,圆C关于直线
,圆C关于直线![]() 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为![]()
①求圆C的方程;
②已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l方程。
19、 (本小题满分12分)
如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=![]() ,
,
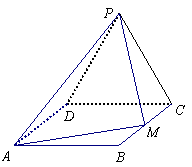 M为BC的中点
M为BC的中点![]()
(Ⅰ)证明:AM⊥PM;
(Ⅱ)求二面角P-AM-D的大小;
(Ⅲ)求点D到平面AMP的距离![]()
20、数列![]() 的前
的前![]() 项和记为
项和记为![]()
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)等差数列![]() 的各项为正,其前
的各项为正,其前![]() 项和为
项和为![]() ,且
,且![]() ,
,
又![]() 成等比数列,求
成等比数列,求![]()
21、(本题满分12分)
已知函数![]()
(1)求证:函数![]() 在(0,
在(0,![]() )上是增函数;
)上是增函数;
(2)若![]() 在[1,
在[1,![]() ]上恒成立,求实数a的取值范围;
]上恒成立,求实数a的取值范围;
22、(本小题14分)
已知中心在原点的双曲线![]() 的右焦点为抛物线
的右焦点为抛物线![]() 的焦点,右顶点为椭圆
的焦点,右顶点为椭圆![]() 的右顶点。
的右顶点。
![]() 求该双曲线
求该双曲线![]() 的方程;
的方程;
![]() 若直线
若直线![]() 与双曲线有两个不同的交点
与双曲线有两个不同的交点![]() ,且
,且![]()
![]() 求
求![]() 的取值范围?
的取值范围?
数学试题参考答案
一、选择题
1——5:CDDAA 6——10:CDBDA 11——12:BD
二、 填空题
13、(2,1) 14、8 15、![]() 16、
16、![]()
三、解答题:
17、(本小题满分12分)
解:(1)![]()
![]() ,
,
![]() (3分)
(3分)
由![]() 得
得![]() 又
又![]()
![]() (6分)
(6分)
(2)由![]() ,得
,得![]()
![]()
![]() (10分)
(10分)
又![]() =
=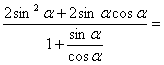
![]() (12分)
(12分)
18、解:(1)![]() (4分)
(4分)
(2)![]() 切线在两坐标轴上的截距相等且不为零,设
切线在两坐标轴上的截距相等且不为零,设![]() (6分)
(6分)
![]() 圆
圆![]()
![]() 圆心
圆心![]() 到切线的距离等于半径
到切线的距离等于半径![]() ,
,
即![]() (8分)
(8分)
![]() 。
。
所求切线方程![]() (12分)
(12分)
19、 (本小题满分12分)
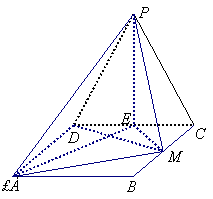 解法1:(Ⅰ) 取CD的中点E,连结PE、EM、EA
解法1:(Ⅰ) 取CD的中点E,连结PE、EM、EA
∵△PCD为正三角形
∴PE⊥CD,PE=PDsin∠PDE=2sin60°=![]()
∵平面PCD⊥平面ABCD
∴PE⊥平面ABCD (2分)
∵四边形ABCD是矩形
∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得
EM=![]() ,AM=
,AM=![]() ,AE=3
,AE=3
∴![]() (3分)
(3分)
![]()
又![]() 在平面ABCD上射影:
在平面ABCD上射影:
∴∠AME=90°
∴AM⊥PM (4分)
(Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM
∴∠PME是二面角P-AM-D的平面角 (6分)
∴tan ∠PME=![]()
∴∠PME=45°
∴二面角P-AM-D为45°; (8分)
(Ⅲ)设D点到平面PAM的距离为![]() ,连结DM,则
,连结DM,则
![]() (10分)
(10分)
∴![]()
而![]()
在![]() 中,由勾股定理可求得PM=
中,由勾股定理可求得PM=![]()
![]()
![]() ,
,
所以:![]() ∴
∴![]()
![]()
即点D到平面PAM的距离为![]()
![]() (12分)
(12分)
解法2:(Ⅰ) ∵四边形ABCD是矩形
∴BC⊥CD
∵平面PCD⊥平面ABCD
∴BC⊥平面PCD (2分)
而PC![]() 平面PCD
平面PCD
∴BC⊥PC, 同理AD⊥PD
在Rt△PCM中,PM=![]()
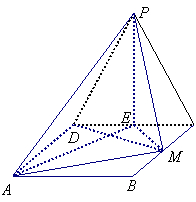 同理可求PA=
同理可求PA=![]() ,AM=
,AM=![]()
∴![]() (3分)
(3分)
∴∠PMA=90°
即PM⊥AM (4分)
|
∵△PCD为正三角形
∴PE⊥CD,PE=PDsin∠PDE=2sin60°=![]()
∴PE⊥平面ABCD
由(Ⅰ) 可知PM⊥AM
∴EM⊥AM
∴∠PME是二面角P-AM-D的平面角 (6分)
∴sin ∠PME=![]()
∴∠PME=45°
∴二面角P-AM-D为45°; (8分)
(Ⅲ)同解法(Ⅰ)
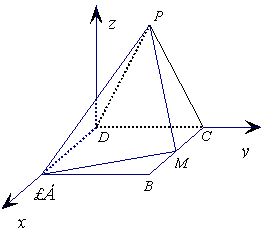
解法3:(Ⅰ) 以D点为原点,分别以直线DA、DC为
x轴、y轴,建立如图所示的空间直角坐标系![]() ,
,
依题意,可得
![]()
![]() ……2分
……2分
∴![]()
![]() (4分)
(4分)
∴![]()
即![]() ,∴AM⊥PM
,∴AM⊥PM![]() (4分)
(4分)
(Ⅱ)设![]() ,且
,且![]() 平面PAM,则
平面PAM,则
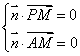 即
即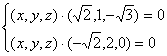
∴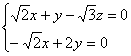
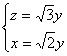
取![]() ,得
,得![]() (6分)
(6分)
取![]() ,显然
,显然![]() 平面ABCD
平面ABCD
∴![]()
结合图形可知,二面角P-AM-D为45°; (8分)
(Ⅲ) 设点D到平面PAM的距离为![]() ,由(Ⅱ)可知
,由(Ⅱ)可知![]() 与平面PAM垂直,则
与平面PAM垂直,则
![]() =
=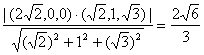
![]()
即点D到平面PAM的距离为![]()
![]() (12分)
(12分)
20. 解:(Ⅰ)由![]() 可得
可得![]() ,
,
两式相减得![]()
又![]() ∴
∴![]()
故![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 得等比数列
(4分)
得等比数列
(4分)
∴![]() (5分)
(5分)
(Ⅱ)设![]() 的公差为
的公差为![]()
由![]() 得,可得
得,可得![]() ,可得
,可得![]() (6分)
(6分)
故可设![]()
又![]()
由题意可得![]()
解得![]() (8分)
(8分)
∵等差数列![]() 的各项为正,∴
的各项为正,∴![]()
∴![]()
∴![]() (12分)
(12分)
21.解:(1)![]()
![]() 在(0,
在(0,![]() )上为增函数 (4分)
)上为增函数 (4分)
(2)![]() 在[1,
在[1,![]() )上恒成立
)上恒成立
设![]()
则![]() 在[1,
在[1,![]() )上恒成立
)上恒成立
![]()
![]() 在[1,
在[1,![]() ]上单调递增
]上单调递增
![]() (10分)
(10分)
故![]() 即
即![]()
![]() 的取值范围为(
的取值范围为(![]() ,3) (12分)
,3) (12分)
22解:
(1)由题意知:双曲线的焦点为(2,0),右顶点为(![]() ,
,![]() ) (
) (![]() 分)
分)
设所求双曲线方程为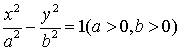 ,
,
则![]()
![]() (
(![]() 分)
分)
![]() 所求双曲线方程为
所求双曲线方程为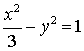 (
(![]() 分)
分)
(2)设![]() ,由
,由
![]()
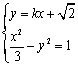 消去
消去![]() 得到:
得到:![]()
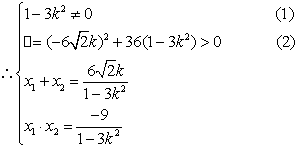 (
(![]() 分)
分)
![]()
![]()
![]()
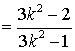 (
(![]() 分)
分)
![]()
![]()
![]()
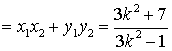 (
(![]() 分)
分)
又![]()
![]()
![]()
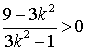 ③
(
③
(![]() 分)
分)
由①②③解得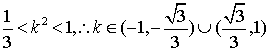 (
(![]() 分)
分)