高三数学选择题分章强化训练（四）
（数列及其极限）
命题人：陈文运
姓名： 学号：
1．在等差数列｛
｝中，若
则
（ ）
（A）1 （B）－1
（C）2 （D）－2
2．已知等比数列｛｝的各项均为正数，公比q
，设
则P与Q的大小关系是（ ）
（A）
（B）
（C）P=Q （D）无法确定
3．等差数列｛｝和｛
｝的前n项的和分别为
和T
，对一切自然数n都有
，则
（ ）
（A）
（B）
（C）
（D）
4．已知数列｛｝的通项公式
则其前n项的和的最小值是（ ）
（A）－784 （B）－392
（C）－389 （D）－368
5．公差不为0的等差数列｛｝中，
依次成等比数列，则公比等于（ ）
（A）
（B）
（C）2 （D）3
6．数列1，，，，，，
，，，，…的前100项的和等于（ ）
（A）
（B）
（C）
（D）
7．非0实数
成等差数列，
与
分别成等比数列，则y＝（ ）
（A）10 （B）12
（C）14 （D）16
8．无穷数列
各项和等于（ ）
（A）1
（B）
（C）
（D）
9．无穷等比数列｛｝中，
设
则
（ ）
（A）
（B）
（C）2 （D）1
10．已知等比数列｛｝中，
则
（ ）
（A）
（B）
（C）6 （D）12
11．数列｛｝既是等差数列又是等比数列，则｛｝是（ ）
（A）公差为0的等差数列 （B）公比为1的等比数列
（C）常数数列
（D）前n项和是二次函数的数列
12．｛｝是项数为偶数的等差数列，它的奇数项之和为24，偶数项之和为30，若它的末项比首项大10.5，则数列的项数是（ ）
（A）6 （B）8
（C）12 （D）16
13．在｛｝中，已知前n项和＝
则
（ ）
（A）69200 （B）1400
（C）1415 （D）1385
14．在－9和3之间插入n个数，使这n＋2个数组成和为－21的等差数列，则n的值为（ ）
（A）4 （B）5
（C）6 （D）7
15．已知等比数列｛｝，又第m项至第n项的和为720（m<n），则m的值为（ ）
（A）3 （B）5
（C）6 （D）7
16．已知等差数列｛｝，表示前n项的和，
则
中最小的是（ ）
（A）S
（B）
（C）S
（D）
17．在各项均为正数的等比数列｛｝中，
则
（ ）
（A）12 （B）10
（C）8
（D）2＋
18．已知等比数列｛｝，首项为
，公比为q，则｛｝为递增数列的充要条件是（ ）
（A）
（B）
且
（C）且
（D）
或
19．等差数列｛｝中，表示前n项的和，若
，则
（ ）
（A）
（B）
（C）
（D）
20．公差不为0的等差数列的第二、三、六项构成等比数列，则公比为（ ）
（A）1 （B）2
（C）3 （D）4
21．在等差数列｛｝中,
若
，则n的最小值为（ ）
（A）60 （B）62
（C）70 （D）72
22．已知非0实数
成等差数列，则二次函数
＋2bx+c的图象与x轴的交点个数为（ ）
（A）1 （B）2
（C）1或2 （D）0
23．等差数列｛｝中，
数列｛｝是等比数列。已知
则满足不等式
的最小自然数
是（ ）
（A）5 （B）6
（C）7 （D）8
24．已知数列｛｝为等比数列，对于任意
有
则
（ ）
（A）
（B）
（C）
（D）
25．双曲线
（
>0，b>0）的实轴长、虚轴长、焦距成等差数列，则其离心率
等于（ ）
（A）
（B）
（C）2
（D）2
26．下面的数列中，有极限的是（ ）
① －1，0.1，－0.01，0.001，－0.0001，…
② 0，
…
③ 
（A）①和③ （B）②和③
（C）①和② （D）①、②和③
27．下列命题中，正确的是（ ）
（A） 若
则
（B） 若，
则
（C） 若
则
（D） 若
则
28．使
与
的差的绝对值小于
的最小自然数n的值是（ ）
（A）68 （B）79
（C）88 （D）大于100的某数
29．
（ ）
（A）1
（B）
（C）
（D）
30．等比数列｛｝中，公比为q，表示前n项的和。若
则
（ ）
（A）2 （B）1
（C）－1 （D）－2
31．当
时，
（ ）
（A）1 （B）c
（C）
（D）1或
32．若
则r的取值范围是（ ）
（A）
（B）
（C）
（D）
33．
且
存在是
存在的 （ ）
（A）充分不必要条件 （B）必要不充分条件
（C）充分必要条件 （D）既不充分也不必要条件
34．设等差数列｛｝，｛｝的前项的和分别为与
，若，则
＝ （ ）
（A）1
（B）
（C）
（D）
35．
的值是 （ ）
（A）
（B）
（C）1
（D）
36．设等差数列｛｝的首项
，公差
，则
＋…＋
的值是 （ ）
（A）
（B）3
（C）
（D）
37．已知
的展开式的第7项为
，则
的值是（ ）
（A）
（B）
（C）－
（D）－
38．数列的通项＝
，若存在，则
的取值范围是 （ ）
（A）
（B）
（C）
（D）
39．某个命题与正整数有关，若当
时该命题成立，那么可推得当
时该命题也成立，现已知当
时该命题不成立，那么可推得 （ ）
（A）当
时，该命题不成立
（B）当时，该命题成立
（C）当
时，该命题成立
（D）当时，该命题不成立
40．若三数
成等差数列，且
又成等比数列，则
的值是（ ）
（A）0 （B）1 （C）0或1 （D）不存在
41. 已知集合Ａ＝｛１，２，４，８，…，２ｎ｝（ｎ≥３，ｎ∈Ｎ），集合A中含有三个元素的所有子集依次为Ｂ１，Ｂ２，…，Ｂｍ.若Ｂｉ中所有元素之和为ａｉ（ｉ＝１，２，…，ｍ）则
(A)2 (B)1 (C)0 (D)不存在
42．已知数列
的通项公式为
=
，其中a、b、c均为正数，那么与
的大小是
（
）
A．>
B． < C． = D. 与n的取值有关
43.已知数列{}的前n项和
其中a、b是非零常数，则存在数列{
}、{
}使得（ ）
A．
为等差数列，{}为等比数列
B．和{}都为等差数列
C．
为等差数列，{}都为等比数列
D．和{}都为等比数列
44.将正偶数按下表排成5列：
第1列 第2列 第3列 第4列 第5列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
…… …… 28 26
则2004在 （ ）
A．第251行，第1列 B．第251行，第3列
C．第250行，第2列 D．第250行，第5列 ．
45. 11．{an}为公比不为1的正项等比数列，则 （ ）
A．a1+a8>a4+a5 B．a1+a8<a4+a5
C．a1+a8=a4+a5 D．a1+a8与a4+a5大小不定
46. 
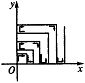如图，一个粒子在第一象限运动，在第一秒内，它从原点运动到(0，1)，而后它接着按图所示在x轴、y轴的平行方向来回运动(即(0，0)→(0，1)→(1，1)→(1，O)→(2，O)→…)，且每秒移动一个单位长度，那么2004秒时，这个粒子所处位置为
A.(20，44) B.(21，44)
C.(44，20) D.(44，21)
47.
等于
A.
B.0
C.
D.不存在
48.利用数学归纳法证明(n+1)(n+2)…(n+n)=2n·1·3·…·(2n-1)时，由k到k+1左边应添加的因式是
A.2k+1
B.
C.
C.
答案:
CABBD ABBAA BBDBA BBDDC BCCDB CCBCA ABABB ACDDC CBCBA ACC
46.A 研究粒子到达点(0，n)时所用秒数，当n为奇数时，恰好用n2秒；当n为偶数时，用时为(n+1)2-1秒.
47.C
将分子局部有理化，原式=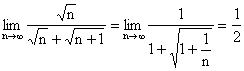
.
48.C 注意观察第一个数及最后一个数的特征.