高三数学选择题分章强化训练（一）

高三数学选择题分章强化训练（一）

(集合、简易逻辑与函数)

命题人：陈文运

姓名：　　　　　　　　　　  学号：

1．已知全集I＝｛x│x＝，mN｝，A＝｛x│x＝，nN｝，B=｛x│x＝()，nN｝，那么　　  （　　　 ）

（A）AB＝　　　　　　　　　　　　　　 （B）B＝

（C）A＝　　　　　　　　　　　　　  （D）＝　　

2．函数y＝的值域为　　　　（　　　）

（A）　　　　　　　　　　　　　　  （B）

（C）　　　　　　　　　　　　　　　 （D）

3．设f (x ) 是定义在R上的函数，且在（－）上是增函数，　又 F（x ）＝f (x)－f (－x)，那么F（x ）一定是　　　　　　　 （　　　 ）

（A）　　　奇函数，且在（－）上是增函数；

（B）　 奇函数，且在（－）上是减函数；

（C）　 偶函数，且在（－）上是增函数；

（D）　偶函数，且在（－）上是减函数；

4．函数y＝log(6－x－x)的单调递增区间是　　　　  （　　　　）

（A）　　　　　　　　　　　　　　 　（B）

（C）　　　　　　　　　　　　　　　　 （D）

5．函数y＝log（x＋＋1）　　（x > 1）的最大值是　　（　　 ）

（A）－2　　　　　　　　　　　　　　　　　　 （B）2

（C）－3　 　　　　　　　　　　　　　　　　　（D）3

6．若把函数y＝f(x)的图象作平移，可以使图象上的点P(1, 0)变换成点Q（2，2），则函数y＝f(x)的图象经此变换后所得图象对应函数为　 （　　　　 ）

（A）y＝f(x－1)＋2　　　　　　　　　　　　　  （B）y＝f(x－1)－2　

（C）y＝f(x＋1)＋2　　　　　　　　　　　　　　（D）y＝f(x＋1)－2

7．已知y＝f(x)存在反函数，且y＝f(x＋1) 的图象过（0，2），那么下列函数中，可能

是y＝f(x)的反函数的是　（　　　 ）

（A）y＝1＋　（0x2）　　　　 （B）y＝1－　（－2x2）

（C）y＝2－　（0x2）　　　 　　 （D）y＝　（0x2）

8．设＜()＜（）＜1，那么　（　　 ）

（A）a＜a＜b　　　　　　　　　　　　　 （B）a＜ b＜a

（C）a＜a＜b　　　　　　　　　　　　　 （D）a＜b＜a

9．定义在R上的奇函数f (x )满足f (3＋x )＝f (3－x )，若当x（0，3）时，f ( x )＝2，则当x（－6，－3）时，f ( x )的解析式为　 （　　　 ）

（A）2　　　　　　　　　　　　　　　　 （B）－2

（C）2　　　　　　　　　　　　　　　　 （D）－2

10．已知log（3a－1）恒为正数，那么实数的取值范围是 （　　　　 ）

（A）a＜　　　　　　　　　　　　　　　　 （B）＜a

（C）a＞1　　　　　　　　　　　　　　　　  （D）＜a＜或a＞1

11．函数f (x )＝的奇偶性及单调性的情况是 （　　　　）

（A）增函数、偶函数　　　　　　　　　　　 （B）减函数、奇函数

（C）增函数、非奇非偶函数　　　　　　　　 （D）减函数、非奇非偶函数

12．为了得到函数y＝f (－2x )的图象，可以把函数y＝f (1－2x )的图象适当平移，这个平移是 （　　）

（A）沿x轴向右平移1个单位　　　　　　　 （B）沿x轴向右平移个单位

（C）沿x轴向左平移1个单位　　　　　　　 （D）沿x轴向左平移个单位

13．映射f：XY使任意xX,都有y＝x，yY．集合X、Y可以是 （　　  ）

（A）X＝R，Y＝　　　　　  　　　　　　（B）X＝Y，Y＝R

（C）X＝，Y＝R　　　　　　　　　　　 （D）X＝，Y＝

14．函数y＝f ( x )的图象关于x轴对称，这样的函数数目有 （　　　 ）

（A）0　　　　　　　　　　　　  　　　　　 （B）1

（C）2　　　　　　　　　　　　　　　　　　 （D）无数多个

15．全集为R，集合M＝｛x│x9｝，集合S＝｛x│x－3x＋2≥0｝，则∩S＝（　　　　）

（A）∪　　　　　　　　　　  （B）∪

（C）∪　　　　　　　　　　　  （D）∪

16．定义在R上的函数y＝f ( x )，对任何x∈R都有f ( x )＋f (－x )＝1，这个函数的图象的几何特征是 （　　 ）

（A）关于原点对称　　　　　　　　　　　　　  （B）关于y轴对称

（C）关于点（0，1）对称　　　　　　　　　　  （D）关于点（0，）对称

17．函数y＝f ( x )的定义域和值域都是R，则函数y＝－f (－ x )的图象位置是 （　　）

（A）在第一象限　　　　　　　　　　　　　　  （B）在第二象限

（C）在第三象限　　　　　　　　　　　　　　  （D）在第四象限

18．函数y＝f ( x )的图象与直线x＝1的公共点数目是 （　　　）

（A）1　　　　　　　　　　　　　　　　　　　 （B）0

（C）0或1　　　　　　　　　　　　　　　　　 （D）1或2

19．函数y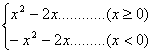＝这个函数的奇偶性是 （　　　）

（A）偶函数　　　　　　　  　　　　　　　　　（B）奇函数

（C）既是奇函数又是偶函数　　　　　　　　　  （D）非奇非偶函数

20．有三个函数，第一个函数是y＝f ( x )，第二个函数是第一个函数的反函数 y＝

f ( x )，第三个函数与第二个函数的图象关于点（1，0）对称。第三个函数是 （　　　 ）

（A）函数y＝f ( 2－x )的反函数　　　　　　　　 （B）函数y＝f ( x )＋2的反函数

（C）函数y＝2－f ( x )的反函数　　　　　　　 　（D）函数y＝f ( x )－2的反函数

21．函数y＝x的奇偶性和单调性的情况是 （　　）

（A）偶函数，在（－，0）上是减函数　　

（B）偶函数，在（－，0）上是增函数

（C）奇函数，在（－，0）上是减函数

（D）奇函数，在（－，0）上是增函数

22．奇函数y＝f ( x )在x < 0时，f ( x )＝2＋x－1，则在x≥0时函数的解析式是（　 ）

（A）f ( x )＝2－x＋1　　　　　　　　　　　　 （B）f ( x )＝－2＋x－1

（C）f ( x )＝2＋x－1　　　　　　　　　　　　 （D）f ( x )＝－2－x＋1

23．已知a、b、c＞0，a、b、c1，x＞0，abc1，logx＝b，logx＝c，logx＝a，则logx的值是 （　　　 ）

（A）＋＋　　　　　　　　　　　　　　　 （B）a＋b＋c

（C）　　　　　　　　　　　　　　　　　 （D）

24．集合M满足条件｛3，4｝M｛0，1，2，3，4｝，这样的集合M的数目是（　）

（A）1　　　　　　　　　　　　　　　　　　　 （B）2

（C）7　　　　　　　　　　　　　　　　　　　 （D）8

25．集合M＝｛x︱x，xQ｝，S＝｛x︱x＝p＋q，p、qQ｝，这两个集合的关系是 （　　）

（A）M＝S　　　　　　　　　　　　　　　　　 （B）MS

（C）SM　　　　　　　　　　　　　　　　　 （D）M∩S＝

26．奇函数y＝f ( x )的反函数为函数y＝f ( x )，函数y＝f ( x )在上是减函数，则函数y＝－f ( x )在（－，0）上是 （　　 ）

（A）增函数　　　　　　　　　　　　　　　　  （B）减函数

（C）非单调函数　　　　　　　　　　　　　　  （D）不能确定

27．函数，则函数是（　　 ）

（A）　　  奇函数且在区间上单调递减

（B）　　  偶函数且在区间上单调递增

（C）　　  奇函数且在区间上单调递减

（D）　　 偶函数且在区间上单调递增

28．c＜0，下列不等式中正确的是 （　　　　）

（A）c2　　　　　　　　　　　　　　　 （B）c＞（）

（C）2＜（）　　　　　　　　　　　　 （D）2＞（）

29．函数f ( x )＝a （a＞1，x＞0），下列命题中的假命题是　（　　　 ）

（A）f (logx)＝logf ( x )　　　　　　　　  （B）f ( x )＝logf [f ( x )]

（C）f (a)＝a　　　　　　　　　　　　 （D）[f (a)] ＝a

30．a(，1)∪（1，＋），x＝︱log2︱，y＝log2，z＝log2，则x、y、z的大小关系是　（　　　　）

（A）x＞y＞z　　 　　　　　　　　　　　　　　（B）z＞y＞x

（C）y＞z＞x　　　　　　　　　　　　　　　　 （D）x＞z＞y

31．x（1，＋∞）时，x＞x，则、的大小关系是　（　　）

（A）︱︱＞︱︱　　　　　　　　　　　　  （B）＞

（C）0  （D）＞0＞

32．定义在R上的函数y＝f ( x )有反函数y＝f ( x )，则函数y＝f ( x＋a )＋b的图象与函数y＝f ( x ＋a)+b的图象间的关系是　（　　 ）

（A）关于直线y＝x＋a－b对称　　　　　　 （B）关于直线y＝x＋a＋b对称

（C）关于直线y＝x－a－b对称　　　　　　 （D）关于直线y＝x－a＋b对称

33．已知集合P、Q满足P∩Q＝｛1，2｝，P∪Q＝｛1，2，3，4，5｝，I＝N，则（P∪Q）∩（∪）为　（　　　 ）

（A）｛1，2，3｝　　　　　　　　　　　　　　 （B）｛2，3，4｝

（C）｛3，4，5｝　　　　　　　　　　　　　　 （D）｛1，4，5｝

34．集合A＝｛1，2，3，a｝，B＝｛3，a｝，则使A∪B＝A成立的a的个数是（　　）

（A）2个　　　　　　　　　　　　　　　　　 （B）3个

（C）4个　　　　　　　　　　　　　　　　　 （D）5个

35．如果（x，y）在映射f下的像是（，），则（－5，2）在f作用下的原像是（　　　　 ）

（A）（－10，4）　　　　　　　　　　　　　 　（B）（－3，－7）

（C）（－6，－4）　　　　　　　　　　　　　  （D）（－，－）

36．设全集I＝R，集合M＝｛x︱＞2｝，N＝｛x︱log7＞log7｝，那么M∩＝（　　　　）

（A）（－，－2）　　　　　　　　　　　　　 （B）（－∞，－2）∪

（C）　　　　　　　　　　　　　　　　 （D）

37．设集合A＝｛x︱︱x︱<2｝，B=｛x︱xa｝，若AB ，则有 （　　　　 ）

（A）a＞2　 　　　　　　　　　　　　　　　　（B）a2

（C）a2　　　　　　　　　　　　　　　　　 （D）a＜2

38.函数y＝＋1　 （x2）的反函数是　（　　　　  ）

（A）y＝2－（x－1）　 （x2）　　　　　  （B）y＝2＋（x－1） （x2）

（C）y＝2－（x－1）　 （x1）　　　　　  （D）y＝2＋（x－1） （x1）

39．已知函数f ( x )定义在R上，且对任意的x、y∈R，满足f ( x＋y )＝f ( x )＋f ( y )，则函数f ( x )一定是 （　　　 ）

（A）奇函数　　　　　　　　　　　　　　　  （B）偶函数

（C）既是奇函数又是偶函数　　　　　　　　  （D）非奇非偶函数

40．设函数f ( x )＝2x＋3，g (x＋2)＝f ( x )，则g ( x )的表达式是 （　　）

（A）2x＋1　　　　　　　　　　　　　　　　 （B）2x－1

（C）2x－3　　　　　　　　　　　　　　　　 （D）2x＋7

41．若A、B是两个集合，则下列命题中真命题是（　　 ）

（A） 如果，那么　　  （B）如果,那么

（C）如果，那么　　　 （D）如果,那么

42．命题“方程的解集是”中，使用逻辑连结词的情况是（　　）

（A） 没有使用逻辑连结词　　　　　　　　  （B） 使用了逻辑连结词“或”

（C）使用了逻辑连结词“且”　　　　　　　 （D） 使用了逻辑连结词“非”

43．命题“若，则”的逆命题是（　　）

（A） 若，则A　　　　　　　　 （B） 若，则

（C） 若A，则　　　　　　　　 （D）若，则

44．命题“若，则”的否命题是（　　）

（A）若，则　　　　　 （B） 若，则

（C）若，则　　　　  （D）若，则

45．命题“若，则”的逆否命题是（　　）

（A） 若，则　　　　　  （B） 若，则

（C） 若，则　　　　　  （D） 若，则

46．已知，则下列判断中，错误的是（　　）

（A） 或为真，非为假 　　　　　　　 （B） 或为真，非为假

（C） 且为假，非为假　　　　　　　  （D） 且为假，或为真

47. 已知f(x)是定义在R上的偶函数，若g(x)是奇函数，且g(x)=f(x-1),g(2)=2001,则f(1999)的值等于　(　　)　　　

 (A) －２０００　 　　　　　　　　　　　　　　(B) －２００１　

 (C) ２０００　 　　　　　　　　　　　　　　　(D) ２００１

48. 设为偶函数，且恒成立，时，，则时，(　　)

（A）　 （B）　 （C）　 （D）

49. 有一件商品的成本为1000元，若在月初出售，可获利100元，然后将本利存入银行(已知银行月息为2%)；若在下月初出售，可获利120元，但要付5元保管费，则

 (Ａ)本月初出售获利大　　　　 (B)在下月初出售获利大

(C)在本月初出售和在下月初出售获利相同

(D)在本月初出售和在下月初出售获利大小不能确定

50．ABCD为四边形，动点p沿折线BCDA由点B向A点运动，设p点移动的路程为x，

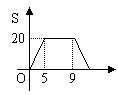△ABP的面积为S，函数S=f（x）的图象如图，给出以下命题：

①ABCD是梯形；

14

②ABCD是平行四边形；　　　　　　　　　　　　　　　　

③若Q为AD的中点时，那么△ABQ面积为10；　　　　　

④当9x14时，函数S=f（x）的解析式为56－4x.　　

其中正确命题为　　　　　　　　　　　　　　　　　　　　

A．①②　　　　　 B．②③　　　　　  C．②④　　　　　 D．①③④

答案:BBABA  AACBD　CDADB　DACBB　BDCCC　ADCDA　BBCCB　BCDAB　ABBAD　ABCAD