高三数学第二次月考试卷
总分150分
一.选择题(满分50分)
1.已知向量![]() ,
,![]() ,则向量
,则向量![]() 与
与![]()
A.互相平行
B.互相垂直
C.夹角为![]() D.夹角为
D.夹角为![]()
2.椭圆![]() 的右焦点到直线
的右焦点到直线![]() 的距离是
的距离是
A.![]() B.
B.![]() C.1
D.
C.1
D.![]()
3.已知![]() ,
,![]() ,当
,当![]() 时,代数式
时,代数式![]() 的值是
的值是
A.正数 B.负数 C.![]() D.介于
D.介于![]() 与
与![]() 之间
之间
4.设![]() 是椭圆的两个焦点,点P是椭圆短轴的顶点,且
是椭圆的两个焦点,点P是椭圆短轴的顶点,且![]() ,则椭圆的离心率e的值是
,则椭圆的离心率e的值是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
5.若x∈[-![]() ],则函数
],则函数![]() 的最小值是
的最小值是
A.1
B.-1
C.-![]() D.-2
D.-2
6.已知等差数列![]() 的公差
的公差![]() , 若
, 若![]() ,
, ![]() , 则该数列的前n项和
, 则该数列的前n项和![]() 的最大值为( )
的最大值为( )
A. 50 B. 45 C. 40 D. 35
7.若实数![]() 、
、![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.直线![]() 曲线
曲线![]() ,则b的值为
,则b的值为
A.3 B.-3 C.2 D.-2
9.设F1、F2是双曲线![]() 的两个焦点, 点P在双曲线上, 且
的两个焦点, 点P在双曲线上, 且![]() ·
·![]()
![]()
![]() ·
·![]()
![]() , 则a的值等于
, 则a的值等于
A. 2 B. 1
C. ![]() D.
D.
![]()
10.直线![]() 与圆
与圆![]() 相切,并且在两坐标轴上的截距之和等于
相切,并且在两坐标轴上的截距之和等于![]() ,则直线
,则直线![]() 与两坐标轴围成的三角形的面积等于
与两坐标轴围成的三角形的面积等于
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
二.填空题(满分30分)
11.已知双曲线的渐近线方程是y=±x,焦点在坐标轴上,焦距是10,则它的方程为 ▲ 。
12.已知![]() ,则
,则![]() 的值为____▲___________
的值为____▲___________
13.
{an}是等差数列,![]() ,{bn}是等比数列,
,{bn}是等比数列,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的通项公式是
的通项公式是![]() ____▲______________
____▲______________
14. .若把圆![]() 按向量a=(1,2)平移后,恰好与直线x一2y+λ=0相切,则实数λ的值为 ▲
按向量a=(1,2)平移后,恰好与直线x一2y+λ=0相切,则实数λ的值为 ▲
15.已知正数x、y满足x+2y=1,则![]() 的最小值是
▲
.
的最小值是
▲
.
16.已知椭圆![]() 与双曲线
与双曲线![]() 具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为
▲
.
具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为
▲
.
17.(满分12分)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边是
所对的边是![]() 、
、![]() 、
、![]() ,且
,且![]() .(1)求
.(1)求![]() 值 ;(2)若
值 ;(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
18.(满分14分)已知函数![]() (a、b、c为常数)的导函数为
(a、b、c为常数)的导函数为![]() ,其分别在
,其分别在![]() 处取得极值。(1)求a、b的值;
处取得极值。(1)求a、b的值;
(2)解不等式![]()
19.(本小题共14分)已知两点![]() ,且动点
,且动点![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求点![]() 的轨迹
的轨迹![]() ;
;
(2)设![]() 、
、![]() 分别是直线
分别是直线![]() 与
与![]() 上的两点,且
上的两点,且![]() 是直线
是直线![]() 的方向向量,直线
的方向向量,直线![]() 与曲线
与曲线![]() 相切,当
相切,当![]() 是以
是以![]() 为底边的等腰三角形时,求
为底边的等腰三角形时,求![]() 的值.
的值.
20.(满分14分)如图, ![]() ,
, ![]() 是双曲线C的两焦点, 直线
是双曲线C的两焦点, 直线![]() 是双曲线C的右准线, A1,
A2双曲线C的两个顶点, 点P是双曲线C右支上异于A2的一动点, 直
是双曲线C的右准线, A1,
A2双曲线C的两个顶点, 点P是双曲线C右支上异于A2的一动点, 直
线A1P,A2P交双曲线C的右准线分别于M, N两点.
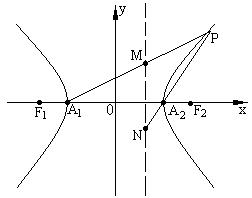 (1) 求双曲线C的方程;
(1) 求双曲线C的方程;
(2) 求证: ![]() 是定值.
是定值.
21.(满分16分)设Sn是数列![]() 的前n项和,且
的前n项和,且![]() .(1)求数列
.(1)求数列![]() 的通项公式;(2)设数列
的通项公式;(2)设数列![]() 使
使![]()
![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)设![]() ,且数列
,且数列![]() 的前n项和为Tn,试比较Tn与
的前n项和为Tn,试比较Tn与![]() 的大小.
的大小.
第二次月考答案
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.B 2. A 3.B 4. A 5. A 6. B 7. D 8.A
9.B 10. A
第Ⅱ卷
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.
11.![]() 12.
12.![]() 13.
13. ![]() 14.3或13
14.3或13
15.
![]() 16.
16. ![]()
三、解答题:本大题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤.
17.(本小题共12分)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边是
所对的边是![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
(1)求![]() 值 ;
值 ;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
(1)![]()
![]() ,
,![]() ,
,
![]() 2分
2分
由![]() ,
,
![]()
![]() ;
;![]() 6分
6分
(2)![]()
![]() ,且
,且![]() ,
,![]()
![]() ,
,
又![]() ,
,![]() ,
,
![]() 9分
9分
![]() .
.
![]() 11分
11分
当切仅当![]() 时,
时,![]() 面积取最大值,最大值为
面积取最大值,最大值为![]() .
. ![]() 12分
12分
18.
(1)∵![]()
∴![]() ……………………………………………………… … 2分
……………………………………………………… … 2分
又∵![]() 在
在![]() 处取得极值
处取得极值
∴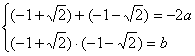 ……………………………………………… 4分
……………………………………………… 4分
解得 a = 1,b = ―1……………………………………………………………… 5分
(2)不等式![]()
即 ![]()
等价于![]() ……………………………………………………… 7分
……………………………………………………… 7分
即![]() ……………………………………………………… 9分
……………………………………………………… 9分
所以原不等式解集为![]() ………………………… 12分
………………………… 12分
19.(1)设![]() ,由
,由![]() ,得
,得
![]() ,
,![]()
![]() ,
,![]() 3分
3分
于是,![]() ,
,![]() ,
,![]() 成等差数列等价于
成等差数列等价于
![]()
![]()
![]()
![]() 6分
6分
所以点![]() 的轨迹是以原点为圆心,
的轨迹是以原点为圆心,![]() 为半径的圆;
为半径的圆;
![]() 7分
7分
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() 、
、![]() ,
,
![]() 直线
直线![]() 与曲线
与曲线![]() 相切,
相切,![]()
![]() ,即
,即![]()
![]() ①,
①, ![]() 9分
9分
由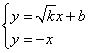
![]()
![]() ,同理
,同理![]() ,
,
![]() 的中点
的中点![]() ,
,
![]() 10分
10分
![]()
![]() 是以
是以![]() 为底边的等腰三角形,
为底边的等腰三角形,
![]() ,即
,即![]()
![]() ②,
②,
![]() 12分
12分
由①②解得![]() .
.
![]() 14分
14分
20.解: (1)由已知, ![]() ∴
∴![]()
所以求双曲线C的方程为![]() …………(4分)
…………(4分)
(2)设P的坐标为![]() , M, N的纵坐标分别为
, M, N的纵坐标分别为![]() …………(5分)
…………(5分)
∵![]() , ∴
, ∴![]()
![]()
![]()
![]()
![]()
![]() …………(6分)
…………(6分)
∵![]() 与
与![]() 共线, ∴
共线, ∴![]()
![]()
同理![]() …………(8分)
…………(8分)
∵![]()
![]()
![]()
![]()
∴![]() ·
·![]() =
=![]() …………(10分)
…………(10分)
=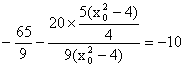 …………(12分)
…………(12分)
21. ∵![]() ,∴
,∴![]() ,
,
于是an+1=Sn+1-Sn=(2 an+1-2)-(2 an-2),即an+1=2an. …………2分
又a1=S1=2 a1-2, 得a1=2. …………1分
∴![]() 是首项和公比都是2的等比数列,故an=2n.
…………1分
是首项和公比都是2的等比数列,故an=2n.
…………1分
(2) 由a1b1=(2×1-1)×21+1+2=6及a1=2得b1=3. …………1分
当![]() 时,
时,![]()
![]() ,
,
∴![]() .
…………2分
.
…………2分
∵an=2n,∴bn=2n+1(![]() ).
).
∴![]()
(3)![]() .
.
![]() .
.