高三数学第二次月考试卷
总分150分
一．选择题（每小题5分，共60分；每小题只有一个正确答案）
1．已知
，
，则复数
在复平面内所对应的点位于（ ）
A. 第一象限 B. 第二象限； C. 虚轴的正向 D. 虚轴的负向．
2．已知
，则下列不等式中成立的是
A．
B．
C．
D．
3．设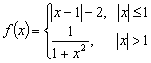
，则f[f(
)]＝(
)
A .
B. 
C. 
D. 
4.
反函数是（
）
A.
B.
C.
D.
5. 设a=
，b=
，c=
，则a, b，c，从小到大排列正确的是（ ）
A .a<b<c B. b<a<c C. c<a<b D. a<c<b
6.下列函数中，值域为（0，+∞）的是（ ）
A．
B．
C．
D．
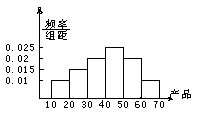
7．一容量为20的样本，其频率分布直方图如右，
则样本在
上的概率为
A．0.09 B. 0.6
C. 0.7 D. 0.9
8. 设0<
<1，则函数
的图象大致形状是（ ）
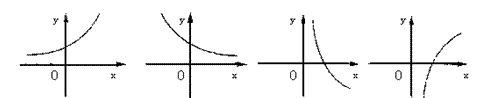
A B C D
9．已知函数
为常数），若
时，
恒成立，则（ ）
A．
B．
C．
D．
10．已知关于
的方程
的两个实根都大于1，则
的范围为（ ）
A．
B．
C．
D．
11．已知函数f(x)满足
，a>0；则
的周期T=（ ）
A．2a B．4 a C．3 a D．6 a
12．对于定义在R上的函数，有下述四个命题，其中正确命题为（
）
①若是奇函数，则
的图象关于点A（1，0）对称；
②若对x∈R，有
，则
的图象关于直线
对称；
③若函数的图象关于直线对称，则为偶函数；
④函数
与函数
的图象关于直线对称。
A．①②④ B．②④ C．①③ D．①③④
二、填空题（本题每小题4分，共16分，只需写出最后结果）
13．已知
，则函数
的最大值为 ；
14．已知函数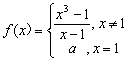
，若在R上连续，则
。
15．盒中有2个白球，3个黑球，从中任取3个球，以
表示取到白球的个数，
表示取到黑球的个数，则
+
=
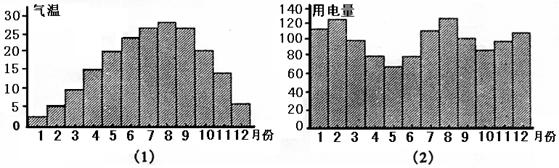
16．一般地，家庭用电量y（千瓦）与气温x（℃）有函数关系
.图（1）表示某年12个月中每月的平均气温，图（2）表示某家庭在12个月中每月的用电量.
试在数集
是2.5的整数倍}中确定一个最小值
和最大值
，使
上的增函数，则区间[，x2]=
.
三、解答题（共6小题，共74分；要求写出必要的文字说明，解题过程和演算步骤）
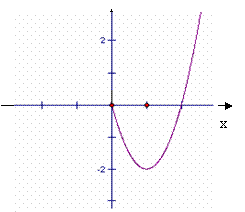17．（本小题12分）已知定义在R上的奇函数，
在
时的图象是如图所示的抛物线的一部分，
1）请补全函数的图象
2）求函数的表达式，
3）说出函数的单调增区间。
18.（本小题12分）
已知不等式
的解集为
1）求a的值； 2）解关于
的不等式
（c为常数）
19. (本大题满分12分）已知定义域为
的函数
（a∈R）是奇函数，
1）求a的值并判断f(x)的单调性
2）若对任意的
，不等式
恒成立，求
的取值范围；
20.（本题满分14分）
某工厂统计资料显示，产品次品率p与日产量n (件)
的关系表如下：
| n | 1 | 2 | 3 | 4 | ┅ | 98 |
| p |
|
|
|
| ┅ | 1 |
又知每生产一件正品盈利a元，每生产一件次品损失
元（
）。 
(1)将该厂日盈利额T（元）表示为日产量n (件)的一种函数关系式；
（2）为了获得最大盈利，该厂的日产量应定为多少件？(精确到1件)
21.（本小题满分12分）
已知函数
在(-1，0)内是增函数，在(0，+
)内是减函数。
1) 实数的值；
2) 当
时，
恒成立，求整数m的最大值
3）0<
时，求证：
；
22．（本小题满分14分）
集合
是由适合以下性质的函数
构成的：
对于任意的
，且
，都有
（1） 试判断
及
是否在集合中？说明理由；
（2） 设
，且定义域是
，值域是
，写出一个满足以上条件的的解析式，并证明你写出的函数
高三第二次月考试题参考答案
一．选择题 CBBABB DAABCC
二．填空题 
； 3； 3； [20，27.5]
三．解答题 17．解：（1）略 (看图给分) ……………………………………4分
（2）当时，设
，又
，得a=2，即
当
时，
，则
8分
所以 = 
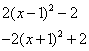
………………………………… 9分
（3）单调递增区间是：
，
……12分
18．解：不等式
可转化为
……………2分
依题意的解集为
∴ 
的两根为1、2
…………………… ………………4分
利用韦达定理不难得
………………………… ………………6分
（2）将代入不等式 得
①当
，原不等式得解集为
……………………………8分
②当
，原不等式得解集为
……………………………………………10分
③当
，原不等式得解集为
…………………………………12分
19．解：1）因为是奇函数，所以
=0，即
，即
…………3分
故
，易知在
上为减函数。……… 6分
2）因是奇函数，从而不等式：
………… 8分
等价于
，因为减函数，由上式推得：
．即对一切有：
，
………………10分
从而判别式
……………………………12分
另：对单调性的判断也可采用求导或定义的方法求解。
20. 解：（1）由题意可知
---------------3分
----------6分.
,
当且仅当
，----------------10分
故
时
取最大值，即
取最大值.------------12分
21解：1）
，依题
，故可得
4分
2）依题
恒成立；即
，令
，
则
9分
易知当
时，
递减；
时，递增
10分
故
，故满足条件的m的最大值-1。 12分
3）因为
，欲证原不等式，只需证明
，其中
，故可令
，则
显然当时
恒成成立，故
在时递增，故
恒成立。
即
恒成立，故原不等式成立。
法二 
由（1）知 
又
22解：见下页
