高三数学第三次限时训练
一、选择题
1、已知![]() ,则
,则![]() 之间的大小关系是
之间的大小关系是
A.m>n B.m<n C.m≥n D.m≤n
2.设f:x→![]() 是集合A到集合B的映射,若B={1,2},则
是集合A到集合B的映射,若B={1,2},则![]()
A.![]() B.{1} C.
B.{1} C.![]() 或{2} D.
或{2} D.![]() 或{1}
或{1}
3.设函数![]() 若
若![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() ∪
∪![]() B.
B.![]() ∪
∪![]()
C.![]() ∪
∪![]() D.
D.![]() ∪
∪![]()
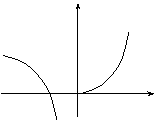
 4.函数
4.函数![]() 的大致图像是
的大致图像是
5.定义在R上的函数![]() 不是常数函数,满足
不是常数函数,满足![]() ,
,![]() ,则函数
,则函数![]()
A.是奇函数也是周期函数 B.是偶函数也是周期函数
C.是奇函数但不是周期函数 D.是偶函数但不是周期函数
6.函数![]() ,(x∈R)的反函数为
,(x∈R)的反函数为
A.![]() , x∈R B.
, x∈R B.![]() ,x∈(0,+∞)
,x∈(0,+∞)
C.![]() , x∈R
D.
, x∈R
D.![]() ,x∈(0,+∞)
,x∈(0,+∞)
7、实数![]() 满足
满足![]() ,则
,则![]() 的值为
的值为
A.8 B.-8 C.8或-8 D.与θ有关
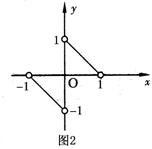 8.函数f(x)的图象是两条直线的一部分(如图2所示),其定义域为
8.函数f(x)的图象是两条直线的一部分(如图2所示),其定义域为![]() ,则不等式f(x)-f(-x)>-1的解集是
,则不等式f(x)-f(-x)>-1的解集是
A.![]()
B.![]()
C.![]()
D.![]()
9.已知函数![]() 对任意实数
对任意实数![]() 都有
都有![]() 成立,若当
成立,若当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.函数![]() 在
在![]() 上是增函数,则
上是增函数,则![]() 的取值范围是
的取值范围是
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
二、填空题
11.设![]() ,那么f(x)的图象关于
对称。
,那么f(x)的图象关于
对称。
12.设二次函数![]() ,如果
,如果![]() ,则
,则![]() =
=
13.已知R为全集,A=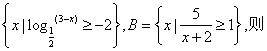 (CRA)∩B是
(CRA)∩B是
14.已知函数![]() ,且满足
,且满足![]() ,
,![]() ,则
,则![]() 的取值范围是
.
的取值范围是
.
15.换成:设函数f(x)的定义域为R,若存在正常数M,使得![]() 对一切实数x均成立,则称f(x)为F函数。给出下列函数:
对一切实数x均成立,则称f(x)为F函数。给出下列函数:
(1)f(x)=x2;
(2)f(x)=![]() ;
;
(3)f(x)=![]()
(4)f(x)=2sinx.
其中是F函数的序号为 。
三、解答题
16.(本题满分12分)
已知![]() 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且![]() ,若
,若![]() ,
,![]() 恒成立.
恒成立.
(1)判断![]() 在[-1,1]上是增函数还是减函数,并证明你的结论;
在[-1,1]上是增函数还是减函数,并证明你的结论;
(2)解不等式![]() ;
;
(3)若![]() 对所有
对所有![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
17.(本题满分12分)
已知函数![]() 的图象与函数
的图象与函数![]() 的图象相切,记
的图象相切,记![]()
![]()
(1)求实数![]() 的值及函数
的值及函数![]() 的极值;
的极值;
(2)若关于![]() 的方程
的方程![]() 恰有三个不等的实数根,求实数
恰有三个不等的实数根,求实数![]() 的取值范围
的取值范围![]()
18.(本题满分12分)
已知函数![]() ,过其上一点P(1,f(1))的切线方程恰为
,过其上一点P(1,f(1))的切线方程恰为![]() 。
。
(1)求![]() 的解析式。
的解析式。
(2)求函数![]() 的定义域和值域。
的定义域和值域。
(3)过![]() 图象上一点Q
图象上一点Q![]() 作
作![]() 的切线L分别交x轴、y轴于M、N两点,O是坐标原点,求ΔMON面积的最小值。
的切线L分别交x轴、y轴于M、N两点,O是坐标原点,求ΔMON面积的最小值。
19、(本题满分14分)
已知函数f(x)=![]() (ax+b)图象过点A(2,1)和B(5,2).
(ax+b)图象过点A(2,1)和B(5,2).
(1)求函数f(x)的解析式;
(2)记![]() ,
,![]() ,是否存在正数k,使得
,是否存在正数k,使得![]() …
…![]() 对一切
对一切![]() 均成立,若存在,求出k的最大值,若不存在,请说明理由.
均成立,若存在,求出k的最大值,若不存在,请说明理由.
参考答案
|
(x<0) (x>0) -1 0 x |
1.A
2.D 集合A中只要含有1或4即可满足题意,此时A∩B为{1}或![]() .
.
3.B 可画出此函数图像,知![]() 轴上方的图像对应的
轴上方的图像对应的![]() 满足
满足![]() .知
.知![]() ∪
∪![]() .
.
4.A
5.B 由![]() ,知
,知![]() ,所以
,所以![]() 以2为周期,再由
以2为周期,再由
![]() 得,
得,![]() .令
.令![]() ,则有
,则有![]() ,∴
,∴![]() 是偶函数.故
是偶函数.故![]() 是偶函数也是周期函数.
是偶函数也是周期函数.
6.A
7.A
 8.D 由函数的图象可知,函数
8.D 由函数的图象可知,函数![]() 是奇函数,所以原不等式可化为2
是奇函数,所以原不等式可化为2![]() ,即
,即![]() ,因而不等式的解集选 D.
,因而不等式的解集选 D.
9.C
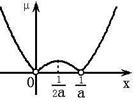
10.A 令![]() ,
,![]() ,
,![]() 的图象如图.当
的图象如图.当![]() 时,由复合函数的单调性可知,区间
时,由复合函数的单调性可知,区间![]() 落在
落在![]() 或
或![]() ,所以
,所以![]() 或
或![]() ,所以有
,所以有![]() .当
.当![]() 时,同理可得
时,同理可得![]()
![]() ,综上选A.
,综上选A.
11.f(x)的图象关于直线x=2对称
12.![]()
13.![]()
14.∵![]() ,∴
,∴![]()
![]() ,
,
∵![]() .
.
又![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
15.②④
(1).当f(x)=x2时,由![]() ,即
,即![]() ,即
,即![]() ,则M不存在;
,则M不存在;
(2).当f(x)=![]() 时,即
时,即![]() ,即
,即![]() =
=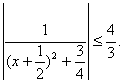 即存在正正常数M,使
即存在正正常数M,使![]() 对一切实数x均成立;
对一切实数x均成立;
(3)当f(x)=![]() 时,取x=0,则
时,取x=0,则![]() ,而
,而![]() ,与
,与![]() 矛盾,故不存在M;
矛盾,故不存在M;
(4)当f(x)=2sinx.,![]() ,当
,当![]() 时,2
时,2![]() ,不妨取M=
,不妨取M=![]() ,式子使
,式子使![]() 对一切实数x均成立;当
对一切实数x均成立;当![]() 时,
时,![]() 也成立,故存在M,使得
也成立,故存在M,使得![]() 对一切实数x均成立;
对一切实数x均成立;
综上所述:应填:(2),(4).
16.(1)设![]()
![]() 是奇函数
是奇函数
∴![]()
由题设知![]() 时,
时,
∴![]() ,
,
即![]()
∴![]()
∴![]() 在[-1,1]上是增函数
在[-1,1]上是增函数
(2)![]() 在[-1,1]上是增函数,不等式等价于
在[-1,1]上是增函数,不等式等价于
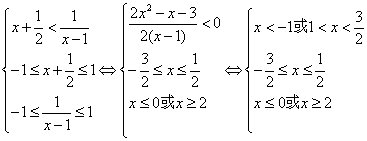
∴![]()
(3)由(1)知,![]() 在[-1,1]上是增函数,且
在[-1,1]上是增函数,且![]()
∴![]()
要![]() ,对所有
,对所有![]() 恒成立,必
恒成立,必![]() 成立
成立
∴![]() 恒成立
恒成立
只要![]() 最小值大于或等于0.
最小值大于或等于0.
①当![]() ∴
∴![]() ∴
∴![]()
②当![]() 恒成立
恒成立
③当![]() 上是减函数,必
上是减函数,必![]() ∴
∴![]()
![]() ∴
∴![]() .
.
综上知,![]()
17.(1)解法一:依题意,令![]()
∴函数![]() 的图象与函数
的图象与函数![]() 的图象的切点为
的图象的切点为![]() ……………2分
……………2分
将切点坐标代入函数![]() 可得
可得 ![]()
![]() ……………4分
……………4分
解法二:依题意得方程![]() ,即
,即![]() 有唯一实数解………2分
有唯一实数解………2分
故![]() ,即
,即![]() ……………4分
……………4分
∴![]() ,
,
故![]() ,
,
令![]() ,解得
,解得![]() ,或
,或![]()
![]() ………………………6分
………………………6分
列表如下:
|
|
|
|
|
|
|
|
|
|
| - |
|
|
|
| 递增 | 极大值 | 递减 | 极小值0 | 递增 |
从上表可知![]() 在
在![]() 处取得极大值
处取得极大值![]() ,在
,在![]() 处取得极小值
处取得极小值![]() ……8分
……8分
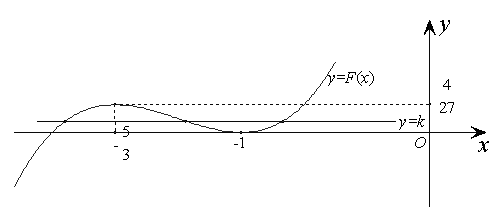 (2)由(1)可知函数
(2)由(1)可知函数![]() 大致图象如下图所示
大致图象如下图所示![]()
![]()
……………………………10分
作函数![]() 的图象,当
的图象,当![]() 的图象与函数
的图象与函数![]() 的图象有三个交点时, 关于
的图象有三个交点时, 关于![]() 的方程
的方程![]() 恰有三个不等的实数根
恰有三个不等的实数根![]()
结合图形可知:![]() ………………………12分
………………………12分
18.(1)∵函数![]() ,∴f’(x)=2ax……2’
,∴f’(x)=2ax……2’
又过其上一点P(1,f(1))的切线方程恰为![]() 。∴2a=1,a=
。∴2a=1,a=![]() ,∴f(x)=
,∴f(x)= ![]()
![]() +b,P(1,
+b,P(1, ![]() +b)代入切线方程得b=-1……4’
+b)代入切线方程得b=-1……4’
∴f(x)= ![]()
![]() -1(
-1(![]() )其反函数
)其反函数![]() ……6’
……6’
(2) ∵![]() =
=![]() ∴其定义域为[-1,1] ……8’
∴其定义域为[-1,1] ……8’
又![]()
∴![]()
∴![]() ……12’
……12’
(3) ∵ 反函数![]() 的
的![]()
∴直线L:![]()
∴M(-![]() -2,0),N(0,
-2,0),N(0,![]() ) ∴
) ∴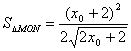 (
(![]() >-1) ……9’
>-1) ……9’
由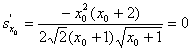 可得
可得![]() =0时,
=0时,![]() ……12’
……12’
19.(1)由已知,得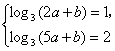 解得:
解得:![]() .∴
.∴![]()
(2)![]() .
.![]()
设存在正数k,使得![]() …
…![]() 对一切
对一切![]() 均成立,则
均成立,则![]() …
…![]() .记
.记![]() …
…
![]() ,则
,则![]()
![]() …
…![]()
![]() .
.
∵![]() .
.
∴![]() ,
,
∴F(n)是随n的增大而增大,
∵![]() ,
,
∴当![]() 时,
时,![]() .
.