高三数学第一次模拟试题(文科)
总分150分
一、选择题:(本大题共10小题,每小题5分,共50分。)
1.已知集合U=R,集合![]()
![]() = (A )
= (A )
A ![]()
![]() B
B ![]()
![]() C
C ![]()
![]() D
D ![]()
![]()
2.设直线 ax+by+c=0的倾斜角为![]() ,且sin
,且sin![]() +cos
+cos![]() =0,则a,b满足( C )
=0,则a,b满足( C )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
3.某医院要在20天内接待8所学校的学生体检,每天只安排一所学校,其中有一所人数较多的学校要连续体检3天,其余学校均只需一天,则在这20天内不同的安排方法为(B )
A. ![]() 种
B.
种
B. ![]() 种
C.
种
C. ![]() 种
D
种
D ![]() 种
种
4. 设等比数列![]() 的前n项和为Sn,若
的前n项和为Sn,若![]() ,则
,则![]() ( C
)
( C
)
A.1:2 B.2:3 C.3:4 D.1:3
5.有关命题的说法错误的是 ( D )
![]() 命题“若
命题“若![]() 则
则
![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() , 则
, 则![]() ”.
”.
![]() “
“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
![]() 对于命题
对于命题![]() :存在
:存在![]() 使得
使得![]() . 则
. 则![]()
![]() :对任意
:对任意![]() 均有
均有![]()
![]() 若
若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题.
均为假命题.
6.在正方体![]() 中,E为正方形ABCD的中心,F为CC1的中点,则EF与AB所成角的正切值为( C )
中,E为正方形ABCD的中心,F为CC1的中点,则EF与AB所成角的正切值为( C )
A.2 B.3
C.![]() D.
D.![]()
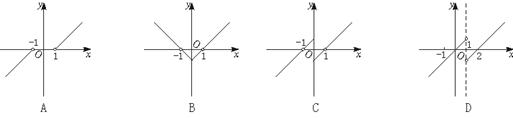
7. 奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为 ( D )
8. 将函数![]() 的图象按向量
的图象按向量![]() 平移后所得图象的解析式是(D)
平移后所得图象的解析式是(D)
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D) ![]()
9. 已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和
![]() .若
.若![]() 是
是![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率是
( A
)
的等差中项,则椭圆的离心率是
( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设数列![]() 的前n项和为
的前n项和为![]() ,令
,令![]() ,称
,称![]() 为数列
为数列![]() ,
,![]() ,……,
,……,![]() 的“理想数”,已知数列
的“理想数”,已知数列![]() ,
,![]() ,……,
,……,![]() 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, ![]() ,
,![]() ,……,
,……,![]() 的“理想数”为
( A
)
的“理想数”为
( A
)
(A) 2002 (B) 2004 (C) 2006 (D) 2008
二、填空题:本大题共4小题,每小题4分,共16分。
11. 设![]() ,则
,则![]() 的值为 1
的值为 1
12.在条件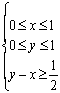 下,则
下,则![]() 的最大值是 3 .
的最大值是 3 .
13.已知![]() 是R上的增函数,如果点A(-1,1)、B(1,3)在它的图象上,
是R上的增函数,如果点A(-1,1)、B(1,3)在它的图象上,![]() 是它的反函数,那么不等式
是它的反函数,那么不等式![]() 的解集为 .
的解集为 .![]()
14.给出如下4个命题:①若α、β是两个不重合的平面,![]() 、m是两条不重合的直线,则α∥β的一个充分而不必要条件是
、m是两条不重合的直线,则α∥β的一个充分而不必要条件是![]() ⊥α,m⊥β,且
⊥α,m⊥β,且![]() ∥m;②对于任意一条直线a,平面α内必有无数条直线与a垂直;③已知命题P:若四点不共面,那么这四点中任何三点都不共线.而命题P的逆否命题是假命题;④已知a、b、c、d是四条不重合的直线,如果a⊥c,a⊥d,b⊥c,b⊥d,则“a∥b”与“c∥d”不可能都不成立.在以上4个命题中,正确命题的序号是__①②④____. (要求将所有你认为正确的命题序号都填上)
∥m;②对于任意一条直线a,平面α内必有无数条直线与a垂直;③已知命题P:若四点不共面,那么这四点中任何三点都不共线.而命题P的逆否命题是假命题;④已知a、b、c、d是四条不重合的直线,如果a⊥c,a⊥d,b⊥c,b⊥d,则“a∥b”与“c∥d”不可能都不成立.在以上4个命题中,正确命题的序号是__①②④____. (要求将所有你认为正确的命题序号都填上)
三、解答题:本大题共6小题,每小题14分,共84分。解答应写出文字说明,证明过程或演算步骤。
15.已知向量![]() ,
,![]() .
.
(Ⅰ)当![]() ⊥
⊥![]() 时,求
时,求![]() +
+![]() 的值;
的值;
(Ⅱ)求函数![]() =
=![]() ·(
·(![]() -
-![]() )的值域.
)的值域.
(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
16.盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意任取3张,每张卡片被抽出的可能性都相等,求:
(Ⅰ) 抽出的3张中有2张卡片上的数字是3的概念;
(Ⅱ) 抽出的3张卡片上最大的数字是4的概率;
(Ⅲ)抽出的3张卡片上的数字互不相同的概率.
解:(I)“抽出的3张中有2张卡片上的数字是3”的事件记为B,则
![]()
(II)“抽出的3张卡片上最大的数字是4”的事件记为A,由题意
![]()
(III)“抽出的3张卡片上的数字互不相同”的事件记为C,“抽出的3张卡片上有两个数字相同”的事件记为D,由题意,C与D是对立事件,因为 ![]()
所以 ![]() .
.
17.设![]() 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为![]() ,且对于所有的正整数n,有
,且对于所有的正整数n,有![]() 。
。
(Ⅰ)写出数列![]() 的前三项;(Ⅱ)求数列
的前三项;(Ⅱ)求数列![]() 的通项公式,并写出推证过程;
的通项公式,并写出推证过程;
(Ⅰ)由题意,当n = 1时,有![]() =
=![]() -2 ,
-2 ,![]() =
= ![]()
∴![]() =
=![]() -2 ,解得
-2 ,解得![]() = 2
= 2
当n =2时,有![]() =
=![]() -2 ,
-2 ,![]() =
= ![]() +
+![]() ,
,
将![]() = 2代入,整理得(
= 2代入,整理得(![]() -2)
-2)![]() =16,由
=16,由![]() >0,解得
>0,解得![]() = 6
= 6
当n = 3时,有![]() =
=![]() -2 ,
-2 ,![]() =
= ![]() +
+![]() +
+![]() ,
,
将![]() = 2,
= 2,![]() = 6代入,整理得(
= 6代入,整理得(![]() -2)
-2)![]() = 64,由
= 64,由![]() >0,解得
>0,解得![]() =10
=10
所以该数列的前三项分别为2,6,10 …………………………………………3分
(Ⅱ)由![]() =
=![]() -2(n∈
-2(n∈![]() ),
),
整理,得![]() =
=![]() ,
,
则![]() =
=![]()
∴![]() =
=![]() -
-![]() =
=![]()
整理,得![]() = 0
= 0
由题意知![]() +
+![]() ≠0,∴
≠0,∴![]() -
-![]() = 4
= 4
∴即数列{![]() }为等差数列,其中首项
}为等差数列,其中首项![]() = 2,公差d = 4 ……………………8分
= 2,公差d = 4 ……………………8分
∴![]() =
= ![]() +(n-1)d = 2 + 4( n – 1 )
+(n-1)d = 2 + 4( n – 1 )
即通项公式为 ![]() =
= ![]() -2,n∈
-2,n∈![]() …………………………………………10分
…………………………………………10分
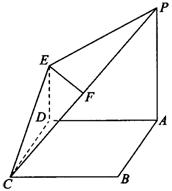
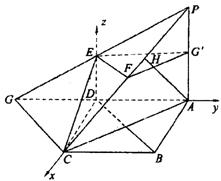
18.如图,四边形ABCD是边长为2的正方形,PA⊥平面ABCD,DE//PA,PA=2DE=AB,F为PC的中点.
|
(2)求平面PCE与平面ABCD所成二面角的余弦值;
(3)求点A到平面PEC的距离.
(1)证法一:取PA中点G′连接EG′、FG′、AC
易得EG′//AD,FG′//AC ………………2分
∴平面EFG′//平面ABCD ∴EF//平面ABCD …………4分
证法二:由条件知DC,DA,DE两两垂直,
∴以DC,DA,DE所在直线为坐标轴建立空间直角坐标系D-xyz
|
D(0,0,0),E(0,0,1),P(0,2,2)
∵F这PC的中点 ∴F(1,1,1)
∵![]() ……2分
……2分
即![]()
又∵![]() 而ABCD 而EF
而ABCD 而EF![]() 面ABCD
面ABCD
∴EF//面ABCD …………4分
(2)解法1 延长PE、AD交于G点,连接GC,
则平面PEC∩平面ABCD=GC
∵![]() ∴GD=DA=DC ∴△ACG为直角三角形
∴GD=DA=DC ∴△ACG为直角三角形
∴GC⊥AC 而AC为PC在平面ABCD内的射影,GC![]() 平面ABCD
平面ABCD
∴由三垂线定理得GC⊥PC
∴∠PCA就是平面PEC与平面ABCD所成二面角的平面角 …………6分
在Rt△PCA中,![]() …………8分
…………8分
解法2 设平面PEC的法向量![]()
∴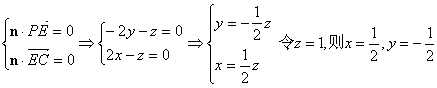
∴![]() …………6分
…………6分
又DE⊥平面ABCD, 即![]() 是平面ABCD的法向量,且
是平面ABCD的法向量,且![]() =(0,0,1)
=(0,0,1)
![]() =1,设平面PEC与平面ABCD的二面角为θ
=1,设平面PEC与平面ABCD的二面角为θ
则 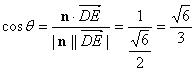 …………8分
…………8分
(3)解法1 作AH⊥PC于H点
由EF//DB,AC⊥DB,PA⊥平面ABCD,PA⊥BD,且AC∩PA=A
∴BD⊥平面PAC ∴EF⊥平面PAC 而AH![]() 平面PAC
平面PAC
∴AH⊥EF 又AH⊥PC EF∩PC=F ∴AH⊥平面PEC
即AH为点A到平面PEC的距离
故在Rt△PCA中有![]() …………12分
…………12分
解法2 由(2)知平面PEC的法向量为n=(![]() )
)
且n=![]()
∴A到平面的距离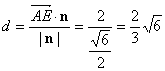 …………
…………
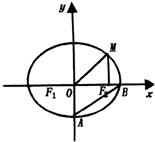
19.如图,![]() 分别是椭圆
分别是椭圆![]() 的左右焦点,M为椭圆上一点,
的左右焦点,M为椭圆上一点,![]() 垂直于
垂直于![]() 轴,且OM与椭圆长轴和短轴端点的连线AB平行,
轴,且OM与椭圆长轴和短轴端点的连线AB平行,
(Ⅰ)求椭圆的离心率;
(Ⅱ)过![]() 且与OM垂直的直线交椭圆于P,Q.若
且与OM垂直的直线交椭圆于P,Q.若![]() ,求椭圆的方程.
,求椭圆的方程.
解:(Ⅰ)由已知![]()
![]()
![]()
![]() ,
,![]()
(Ⅱ) 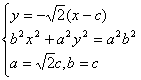
![]()
![]()
![]()
![]()
![]() 椭圆的方程为
椭圆的方程为![]()
20.设函数![]() 、
、![]() R)。
R)。
(1)若![]() ,过两点(0,0)、(
,过两点(0,0)、(![]() ,0)的中点作与
,0)的中点作与![]() 轴垂直的直线,与函数
轴垂直的直线,与函数![]() 的图象交于点
的图象交于点![]() ,求证:函数
,求证:函数![]() 在点P处的切线过点(
在点P处的切线过点(![]() ,0)。
,0)。
(2)若![]() ),且当
),且当![]() 时
时![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
解(1)由已知![]() …………1分
…………1分
![]() …………2分
…………2分
所求,所求切线斜率为![]() …………3分
…………3分
切线方程为![]()
所以,函数y=f (x)过点P的切线过点(b,0) …………4分
(2)因为![]() ,所以
,所以![]() ,
,
![]() …………5分
…………5分
当![]() 时,函数
时,函数![]() 上单调递增,在(
上单调递增,在(![]() ,
,![]() )单调递减,
)单调递减,
在![]() 上单调递增. 所以,根据题意有
上单调递增. 所以,根据题意有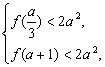 即
即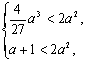
解之得![]() ,结合
,结合![]() ,所以
,所以![]() …………8分
…………8分
当![]() 时,函数
时,函数![]() 单调递增。
…………9分
单调递增。
…………9分
所以,根据题意有![]() …………10分
…………10分
即![]() , 整理得
, 整理得![]() (
(![]() )
)
令![]() ,
,![]()
![]() ,所以“
,所以“![]() ”不等式无解。…13分
”不等式无解。…13分
综上可知:![]() 。
…………14分
。
…………14分