高三数学模拟试卷5

高三数学模拟试卷　　

第Ⅰ卷（选择题　共60分）

参考公式：

如果事件A、B互斥，那么　　　　　　 P(A+B)=P(A)+P(B)　　　　  　　　　　　　

如果事件A、B相互独立，那么　　　　 P(A·B)=P(A)·P(B)　　　　　　　　　 

如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率　　　　 

球的表面积公式　　　其中R表示球的半径

球的体积公式　　　　 其中R表示球的半径

一、选择题（本大题共10小题，每小题5分，共50分.每小题给出的四个选项中，只有一项是符合题目要求的）

1．若sin2α<0，且tanα·cosα<0，则角α在　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．第一象限　　　　　　B．第二象限　　　　　　C．第三象限　　　　　　D．第四象限

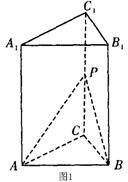
2．如图1所示，正三棱柱ABC—A₁B₁C₁的底面边长为2，

　 高为4，过底面的边AB作一截面交侧棱CC₁于P点，

　 且截面与底面成60°角，则截面△PAB的面积是（　　）

　　　 A．　　　　　　　　 B．

　　　 C．　　　　　　　　　D．

3．若的展开式的第5项是常数项，则正整数n的值为　　　　　　　　　　　　

　　　 A．12　　　　　　　　　　　B．13　　　　　　　　　　　 C．14　　　　　　　　　　　D．15　　　　　　　 （　　）

4．某学习小组共8名同学，其中男生6人女生2人.现从中抽取3名男生1名女生参加某项

　 活动，则不同的抽取方法共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．240种　　　　　　　　B．80种　　　　　　　　　C．70种　　　　　　　　　D．40种

5．设P为△ABC所在平面内一点，且满足，则P是△ABC

　 的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．重心　　　　　　　　　 B．垂心　　　　　　　　　 C．外心　　　　　　　　　 D．内心

6．已知实数x、y满足取得的最小值为－6，则常数m的值为

　　A．－2　　　　　　　　　　　　B．0　　　　　　　　　　　　C．2　　　　　　　　　　　　D．5　　　　　 （　　）

7．已知m、n为两条不同的直线，α、β为两个不同的平面，若m⊥α,n⊥β，则下列命题

　 不正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．若m//n，则α⊥β　　　　　　　　　　　　　　 B．若α⊥β，则m⊥n

　　　 C．若m、n相交，则α、β相交　　　　　　 D．若α、β相交，则m、n相交

8．已知函数f(x)=a^x(a>0，且a≠1)，若f^－1(2)<0，则函数y=f^－1(x+1)的图象中可能是（　　）

9．若椭圆的左、右焦点分别为F₁、F₂，线段F₁F₂被抛物线y²=2bx的焦点F分成3：1两段，则此椭圆的离心率为　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　　　D．

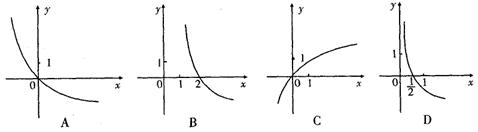
10．设a=sin15°+cos15°，b=sin17°+cos17°，则下列各式正确的是　　　　　　　　　 （　　）

　　　 A．a<<b 　　　　　　　　　　　　　　　　　B．b<<a

　　　 C．a<b< 　　　　　　　　　　　　　　　　　D．b<a<

第Ⅱ卷（非选择题　共100分）

二、填空题（本大题共4小题，每小题5分，共30分.把答案填在题中横线上）

11．在中，角的对边分别为，若，，的面积，那么的外接圆的直径为　　　　 

12．棱长为a的正方体的内切球的体积为　　　　　   .

13．已知圆C：x²+y²－2x+4y=0，则过原点O且与圆C相切的直线方程为　　　　　   .

14．设函数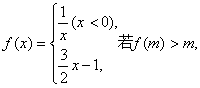则实数m的取值范围是　　　　　　　   .

　　 用区间形式表示）

15．黑、白两种颜色的正六边形地砖按如图2所示产的规律拼成若干个图案：

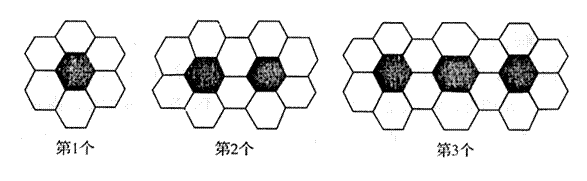　　则第n个图案中有白色地砖　　　　   块.

16．以下四个关于圆锥曲线的命题中

①设A、B为两个定点，k为非零常数，，则动点P的轨迹为双曲线；

②过定圆C上一定点A作该圆的动弦AB，O为坐标原点，若则动点的轨

迹为椭圆；

③方程的两根可分别作为椭圆和双曲线的离心率；

④双曲线有相同的焦点.

　　　 其中真命题的序号为　　　　　　　　 （写出所有真命题的序号）。

三、解答题（本大题共5小题，共70分.解答应写出文字说明、推理过程或演算步骤）

17．（本小题满分14分）

从10个元件中（其中4个相同的甲品牌元件和6个相同的乙品牌元件）随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为，每个乙品牌元件能通过测试的概率均为.试求：

（I）选出的3个元件中，至少有一个甲品牌元件的概率；

（II）若选出的三个元件均为乙品牌元件，现对它们进行性能测试，求至少有两个乙品牌元件同时通过测试的概率.

18．（本小题满分12分）如图，四棱锥P—ABCD的底面边长为1的正方形，PD⊥BC，且PD=1，PC=.

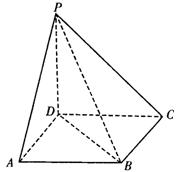
（Ⅰ）求证：PD⊥平面ABCD；

（Ⅱ）求二面角A—PB—D的大小.

19．（本小题满分14分）已知△ABC的周长为6，成等比数列，求

（I）△ABC的面积S的最大值；　　

（Ⅱ）的取值范围.

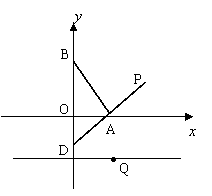20．（本小题满分14分）如图，在平面直角坐标系中，为坐标原点，点，且点是轴上动点，过点作线段的垂线交轴于点，在直线上取点，使

（1）求动点的轨迹的方程

（2）点是直线上的一个动点，过点

作轨迹的两条切线，切点分别为，

求证：

21．（本小题满分16分）设数列满足 a₁=t，a₂=t²，前n项和为S_n，且S_n+2－ (t+1)S_n+1＋tS_n=0(n∈N_＋)．

（Ⅰ）证明数列为等比数列并求的通项公式；

（Ⅱ）当＜t＜2,时，比较与的大小

（Ⅲ）若＜t＜2, ，求证：<．