高三数学模拟试卷(三)
注意:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,时间120分钟。
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若集合![]() ,
,![]() ,则
,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知直线![]() ,直线
,直线![]() 与
与![]() 关于直线
关于直线![]() 对称,则直线
对称,则直线![]() 的斜率为
的斜率为
A.
![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.关于两条直线![]() 与两个平面
与两个平面![]() ,有以下四个命题:
,有以下四个命题:
①若![]() 且
且![]() ,则
,则![]() ;②若
;②若![]() 且
且![]() ,则
,则![]() ;
;
③若![]() 且
且![]() ,则
,则![]() ;④若
;④若![]() 且
且![]() ,则
,则![]() ;
;
其中真命题的个数是
A. 1 B. 2 C. 3 D.4
4.已知![]() 为等差数列
为等差数列![]() 中的第8项,则二项式
中的第8项,则二项式![]() 展开式中常数项是
展开式中常数项是
A. 第7项 B.第8项 C.第9项 D.第10项
5.如果实数![]() 、
、![]() 满足
满足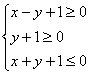 ,那么
,那么![]() 的最大值为
的最大值为
A. 2
B. 1
C. ![]() D.
D.![]()
6.袋中有42个乒乓球,其中红色球3个,蓝色球9个,紫色球12个,黄色球18个,从中随机抽取14个球作成一个样本,则这个样本恰好是按分层抽样方法得到的概率为
A.
![]() B.
B.![]() C.
C.![]() D.
D.![]()
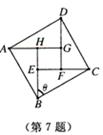 7.2002年8月,在北京召开了国际数学家大会,大会会标为右图所示,它是由四个相同的直角三角形与中间的一个小正方形拼成一个大正方形,若直角三角形有较大的锐角为
7.2002年8月,在北京召开了国际数学家大会,大会会标为右图所示,它是由四个相同的直角三角形与中间的一个小正方形拼成一个大正方形,若直角三角形有较大的锐角为![]() ,大正方形
,大正方形![]() 的面积为
的面积为![]() ,小正方形
,小正方形![]() 的面积为
的面积为![]() ,则
,则![]() 的值等于
的值等于
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
8、![]() 的三内角A,B,C所对边长分别是
的三内角A,B,C所对边长分别是![]() ,设向量
,设向量![]()
![]() ,若
,若![]() ,则角
,则角![]() 的大小为
的大小为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
9、已知![]() 是定义
是定义![]() 在上的偶函数,对任意
在上的偶函数,对任意![]() ,都有
,都有![]() ,若
,若![]() ,则
,则![]() 等于
等于
A. 2007 B. 2006 C. 2 D.0
10、在平面直角坐标系中,定义横坐标及纵坐标均为整数的点为格点。如果直线![]() (
(![]() 不全为0,
不全为0,![]() )与圆
)与圆![]() 的公共点均为格点,那么这样的直线有
的公共点均为格点,那么这样的直线有
A. 24条 B.28条 C.32条 D.36条
第Ⅱ卷(非选择题,共100分)
二、填空题:(本大题共6小题,每小题5分,共30分)把答案填在题中横线上.
11.若函数![]() 在闭区间
在闭区间![]() 上的最大值,最小值分别为
上的最大值,最小值分别为![]() ,则
,则
![]() ▲
▲
12.与双曲线![]() 有共同的渐近线,且经过点
有共同的渐近线,且经过点![]() 的双曲线的一个焦点到一条渐近线的距离等于 ▲
的双曲线的一个焦点到一条渐近线的距离等于 ▲
13.若函数![]() ,其中
,其中![]() 表示
表示![]() 两者中的较小者,则不等式
两者中的较小者,则不等式![]() 的解集为 ▲
的解集为 ▲
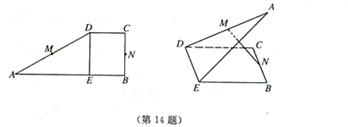
14.如图,设![]() 是直角梯形
是直角梯形![]() 的两腰中点,
的两腰中点,![]() ,现将
,现将![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 为
为![]() ,此时点
,此时点![]() 在平面
在平面![]() 内的射影恰为
内的射影恰为![]() ,则
,则![]() 的连线与
的连线与![]() 所成角为 ▲
所成角为 ▲
15.等差数列有如下性质:若数列![]() 为等差数列,则当
为等差数列,则当![]() 时,数列
时,数列![]() 也是等差数列;类比上述性质,若
也是等差数列;类比上述性质,若![]() 为正项等比数列,则当
为正项等比数列,则当![]() ▲ 时,数列
▲ 时,数列![]() 也是等比数列。
也是等比数列。
16.在直角坐标系![]() 中,已知点
中,已知点![]() ,若点
,若点![]() 在
在![]() 平分线上,且有
平分线上,且有
![]() ,则
,则![]() ▲ 。
▲ 。
三.解答题:(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分,第一小问满分6分,第二小问满分6分)
已知![]() 是两个不共线的向量且
是两个不共线的向量且![]() 。
。
(1)求证:![]() ;
;
(2)若![]() 。
。
18.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为p1,寿命为2年以上的概率为p2.从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
(Ⅰ)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率;
(Ⅱ)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;
(Ⅲ)当p1=0.8,p2=0.3时,求在第二次灯泡更换工作,至少需要更换4只灯泡的概率(结果保留两个有效数字).
19.(本小题满分16分,第一小问满分5分,第二小问满分5分,第三小问满分6分)
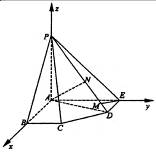
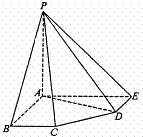 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=![]() a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
(1)求证:PA⊥平面ABCDE;
(2)求二面角A-PD-E的大小;
(3)求点C到平面PDE的距离.
20.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
在直角坐标系中,O为坐标原点,设直线l经过点P(3,![]() ),且与x轴交于点F(2,0).
),且与x轴交于点F(2,0).
(1)求直线l的方程;
(2)如果一个椭圆经过点P,且以点F为它的一个焦点,求椭圆的标准方程;
(3)若在(Ⅰ)(Ⅱ)的情况下,设直线l与椭圆的另一个交点Q,且![]() ,当|
,当|![]() |最小时,求
|最小时,求![]() 对应值.
对应值.
21.(本小题满分14分,第一小问满分3分,第二小问满分5分,第三小问满分5分)
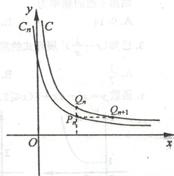
已知曲线C:![]() ,
, ![]() :
:![]() (
(![]() )。从
)。从![]() 上的点
上的点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,再从点
,再从点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,
,
设![]() 。
。
 (I)求
(I)求![]() 的坐标;
的坐标;
(II)求数列![]() 的通项公式;
的通项公式;
(III)记数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]()
高三数学模拟试卷(三)参考答案
一、填空题:每小题5分,满分50分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | A | C | B | C | D | B | C | C |
二、填空题:每小题5分,满分30分.
11.-14 12.2 13.(0,1/2)∪(3,+∞)14.90°15.![]() 16.(-1,2)
16.(-1,2)
三、解答题
17.略(见2007年1-2期中学数学教学参考62页)
18、解:(I)在第一次更换灯泡工作中,不需要换灯泡的概率为![]() 需要更换2只灯泡的概率为
需要更换2只灯泡的概率为![]()
(II)对该盏灯来说,在第1、2次都更换了灯泡的概率为(1-p1)2;在第一次未更换灯泡而在第二次需要更换灯泡的概率为p1(1-p2),故所求的概率为
![]()
(III)至少换4只灯泡包括换5只和换4只两种情况,换5只的概率为p5(其中p为(II)中所求,下同)换4只的概率为![]() (1-p),故至少换4只灯泡的概率为
(1-p),故至少换4只灯泡的概率为

19.(1)证明∵PA=AB=2a,PB=2![]() a,∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
a,∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
同理PA⊥AE.3分∵AB∩AE=A,∴PA⊥平面ABCDE. 5分
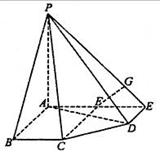 (2)解法一:∵∠AED=90°,∴AE⊥ED.
(2)解法一:∵∠AED=90°,∴AE⊥ED.
∵PA⊥平面ABCDE,∴PA⊥ED.
∴ED⊥平面PAE.过A作AG⊥PE于G,
过DE⊥AG,∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角. 8分
在直角△PAE中,AG=![]() a.在直角△PAD中,AH=
a.在直角△PAD中,AH=![]() a,
a,
∴在直角△AHG中,sin∠AHG=![]() =
=![]() .∴∠AHG=arcsin
.∴∠AHG=arcsin![]() .
.
 ∴二面角A-PD-E的大小为arcsin
∴二面角A-PD-E的大小为arcsin![]() . 10分
. 10分
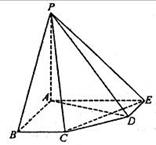
解法二:建立如图所示的直角坐标系,
则B(2a,0,0),E(0,2a,0),P(0,0,2a),D(a,2a,0),C(2a,a,0),
过A作AN⊥PD于N,
∵![]() =(a,2a,-2a),设
=(a,2a,-2a),设![]() =λ
=λ![]() ,
,
∴![]() =
=![]() +
+![]() =(λa,2λa,2a-2λa)
=(λa,2λa,2a-2λa)
∵AN⊥PD,∴![]() ·
·![]() =0.∴a·λa+2a·2λa-2a·(2a-2λa)=0.
=0.∴a·λa+2a·2λa-2a·(2a-2λa)=0.
解得λ=![]() .∴
.∴![]() =(
=(![]() a,
a,![]() a,
a, ![]() a)即
a)即![]() =(-
=(-![]() a, -
a, -![]() a, -
a, -![]() a)
a)
同理,过E作EM⊥PD于M,则![]() =(-
=(-![]() a,
a, ![]() a, -
a, -![]() a). 8分
a). 8分
二面角A-PD-E的大小为![]() ,
,![]() 所成的角<
所成的角<![]() ,
,![]() >.
>.
∵cos<![]() ,
,![]() >=arccos=
>=arccos=![]() .∴<
.∴<![]() ,
,![]() >=arccos=
>=arccos=![]() .
.
∴二面角A-PD-E的大小为arccos![]() . 10分
. 10分
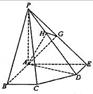 (3)解法一:∵∠EAB=∠ABC=∠DEA=90°, BC=DE=a,AB=AE=2a,
(3)解法一:∵∠EAB=∠ABC=∠DEA=90°, BC=DE=a,AB=AE=2a,
取AE中点F,连CF,
∵AF∥=BC, ∴四边形ABCF为平行四边形.
∴CF∥AB,而AB∥DE, ∴CF∥DE,而DE![]() 平面PDE,CF
平面PDE,CF![]() 平面PDE,
平面PDE,
∴CF∥平面PDE. ∴点C到平面PDE的距离等于F到平面PDE的距离.
∵PA⊥平面ABCDE, ∴PA⊥DE. 又∵DE⊥AE,∴DE⊥平面PAE.
∴平面PAE⊥平面PDE.
∴过F作FG⊥PE于G,则FG⊥平面PDE. ∴FG的长即F点到平面PDE的距离.
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,
 ∴FG=
∴FG=![]() a. ∴点C到平面PDE的距离为
a. ∴点C到平面PDE的距离为![]() a. 16分
a. 16分
解法二:∵PA平面ABCDE,∴PA⊥DE,
又∵∠DEA=90°,∴DE⊥平面PAE,∴DE⊥PE.
∵BC=DE=a,AB=AE=2a,
连接CE,则S△CDE=![]() a2,S△DEP=
a2,S△DEP=![]() a2 .
a2 .
∵VP-CDE=![]() ·PA·S△CDE=
·PA·S△CDE=![]() ·2a·
·2a·![]() a2=
a2=![]() a2.
13分
a2.
13分
 设点C到平面PDE的距离为h,则V C-PDE=
设点C到平面PDE的距离为h,则V C-PDE=![]() ·h·S△PDE=
·h·S△PDE=![]() ·h·
·h·![]() a2=
a2=![]() a2h.∵VP-CDE=VC-PDE, 即
a2h.∵VP-CDE=VC-PDE, 即![]() a3=
a3=![]() a2h, 解得h=
a2h, 解得h=![]() a.即点C到平面PDE的距离为
a.即点C到平面PDE的距离为![]() a. 16分
a. 16分
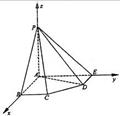
解法三:建立如图所示的直角坐标系,
则B(2a,0,0),E(0,2a,0),P(0,0,2a),
D(a,2a,0),C(2a,a,0),
设平面PDE的一个法向量为n=(x,y,1),∵![]() =(0,2a,-2a),
=(0,2a,-2a),![]() =(-a,0,0),
=(-a,0,0),
又∵n⊥平面PDE.∴n⊥![]() ,n⊥
,n⊥![]() .
.
∴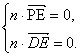 即
即![]() 解得
解得![]() ∴n=(0,1,1). 13分
∴n=(0,1,1). 13分
∵![]() =(-a,a,0),∴cos<
=(-a,a,0),∴cos<![]() ,n>=
,n>=![]()
∵0≤<![]() ,n>≤π,∴<
,n>≤π,∴<![]() ,n>=
,n>=![]() .
.
∵过C作CH⊥平面PDE于H,则CH=![]() ·cos<
·cos<![]() ,n>,
,n>,
即点C到平面PDE的距离为![]() ·cos<
·cos<![]() ,n>=
,n>=![]() a. 16分
a. 16分
20.(1)∵P(3,![]() ),F(2,0),∴根据两点式得,所求直线l的方程为
),F(2,0),∴根据两点式得,所求直线l的方程为![]() =
=![]()
即y=![]() (x-2).∴直线l的方程是y=
(x-2).∴直线l的方程是y=![]() (x-2). 4分
(x-2). 4分
(2)解法一:设所求椭圆的标准方程为![]() =1(a>b>b),
=1(a>b>b),
∵一个焦点为F(2,0),∴c=2.
即a2-b2=4 ①5分∵点P(3,![]() )在椭圆
)在椭圆![]() =1(a>b>0)上,
=1(a>b>0)上,
∴![]() =1 ②7分由①,②解得a2=12,b2=8.
=1 ②7分由①,②解得a2=12,b2=8.
所以所求椭圆的标准方程为![]() =1. 9分
=1. 9分
解法二:设所求椭圆的标准方程为![]() =1(a>b>0),
=1(a>b>0),
∵c=2,a2-b2=4.6分∴椭圆的另一个焦点为F1(-2,0).
由椭圆过点P(3,![]() ),
),
∴2a=PF1+PF2=![]() +
+![]() =4
=4![]() .
.
∴a2=12,b2=8.所以所求椭圆的标准方程为![]() =1. 9分
=1. 9分
(3)解法一:由题意得方程组
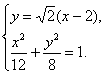 解得
解得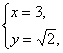 或
或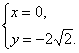 ∴Q(0,2
∴Q(0,2![]() ).11分
).11分
![]() =(-3,-3
=(-3,-3![]() ).∵
).∵![]() =λ
=λ![]() =(-3λ,3
=(-3λ,3![]() λ),
λ),
∴![]() =
=![]() +
+![]() =(3-3λ,
=(3-3λ,![]() ,3
,3![]() λ).∴
λ).∴![]() =
=![]()
=![]() =
=![]() ,
,
∴当λ=![]() 时,
时,![]() 最小. 14分
最小. 14分
解法二:由题意得方程组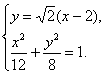 解得
解得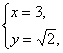 或
或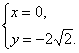
∴Q(0,-2![]() ). ∵
). ∵![]() =λ
=λ![]() =(-3λ,3
=(-3λ,3![]() λ),
λ),
∴点M在直线PQ上,∴![]() 最小时,必有OM⊥PQ.
最小时,必有OM⊥PQ.
∴kOM=-![]() =-
=-![]() .∴直线OM的方程为y=-
.∴直线OM的方程为y=-![]() x.
x.
直线OM与PQ的交点为方程组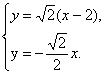 的解,解之得
的解,解之得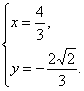
∴M(![]() ,-
,-![]() ),∴
),∴![]() =(-
=(-![]() ,-
,-![]() )
)
∵![]() =λ
=λ![]() ,即(-
,即(-![]() ,-
,-![]() )=λ(-3,-3
)=λ(-3,-3![]() ),∴λ=
),∴λ=![]() .
.
∴当λ=![]() 时,
时,![]() 最小. 14分
最小. 14分
21、(1)由题意得知![]() ,
,![]() ,
,![]() 3分
3分
(2)![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]()
![]() 在曲线
在曲线![]() 上,
上,![]() ,
,![]()
又![]() 在曲线
在曲线![]() 上,
上,![]()
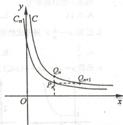
![]()
![]() 8分
8分
(III)![]() ……+
……+![]() …9分
…9分
=![]() =
=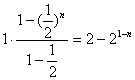
![]()
![]()
![]() ……………………………………12分
……………………………………12分
![]()
![]() ,
,![]()
![]()
![]()
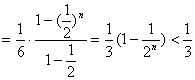 14分
14分