高三上第三次月考数学试卷
总分150分
一、选择题(本大题包括10小题,每小题5分,共50分。每小题恰有一个选项最符合题意。)
1、直线x=-1与直线![]() x+y=0的夹角为:
x+y=0的夹角为:
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2、已知![]() ,
,![]() ,则
,则![]() 的值为
的值为
A.![]() , B.
, B.![]() , C.
, C.![]() , D.
, D.![]()
3、将函数![]() 的图象按向量
的图象按向量![]() 平移后的图象的函数解析式为
平移后的图象的函数解析式为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、已知双曲线![]() ,则双曲线上的点
,则双曲线上的点![]() 到左焦点的距离与点P到左准线的距离之比等于
到左焦点的距离与点P到左准线的距离之比等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、![]() 的展开式中x3的系数是
的展开式中x3的系数是
A.6 B.12 C.24 D.48
6、下列函数中,在其定义域内既是奇函数又是减函数的是
A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]()
7、将棱长相等的正方体按右图所示的形状摆放,从上往下依次为
第1层,第2层,第3 层,…,则第6层正方形的个数是
A.28 B.21 C.15 D.11.
8、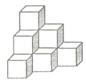 设
设![]() ,
,![]() ,
,![]() 为两两不重合的平面,
为两两不重合的平面,![]() 为两条不重合的直线,给出下列四个命题:
为两条不重合的直线,给出下列四个命题:
①
若![]() 则
则![]() ;②若
;②若![]() 则
则![]() ;
;
③若![]() 则
则![]() ; ④若
; ④若![]() ,则
,则![]() 。其中真命题的个数是
。其中真命题的个数是
A.1 B.2 C. 3 D.4
9、若![]() 则
则![]() 是
是![]() 的
的
A.充分不必要条件,B.必要不充分条件,C.充要条件 ,D既不充分也不必要条件。
10、如果一条直线与一个平面平行,那么,称此直线与平面构成一个“平行线面对”。在一个平行六面体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面对”的个数是
A.60 B.48 C.36 D.24
二、填空题(本大题包括6小题,每小题5分,共30分。)
11、设a 、b为实数,集合M={![]() ,1},N={a,0}, f:x→x表示把集合M是的元素x映射到集合N中仍为x,则a+b的值等于 。
,1},N={a,0}, f:x→x表示把集合M是的元素x映射到集合N中仍为x,则a+b的值等于 。
12、已知![]() 的面积为S,
的面积为S,![]() ,若
,若![]() ,则向量
,则向量![]() 与
与![]() 的夹角的范围是 .
的夹角的范围是 .
13、已知圆![]() 关于直线
关于直线![]() 成轴对称,则
成轴对称,则![]() .
.
14、甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,且a,b![]() {0,1,2,3,…,9},若a-b≤1,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 .
{0,1,2,3,…,9},若a-b≤1,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 .
15、一个正四棱柱的顶点都在球面上,底面边长为1,高为2,则此球的表面积为
16、已知抛物线![]() 过点
过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,则y1+y2的最小值是
。
两点,则y1+y2的最小值是
。
三、解答题(5小题共70分)
17、(本小题12分,第一、二两小问满分各6分)
已知数列![]() 是等差数列,
是等差数列,![]() 是等比数列,且
是等比数列,且![]()
![]() ,
, ![]() ,(I)求数列
,(I)求数列![]() 的通项公式;(II)求数列
的通项公式;(II)求数列![]() 的前10项和
的前10项和![]() 。
。
18、(本小题满分14分,第一小问满分6分,第二小问满分8分)
一个口袋内装有大小相同且已编有不同号码的4个黑球和3个红球,某人一次从中摸出2个球。
(I)如果摸到的球中含有红球就中奖,那么此人中奖的概率是多少?
(II)如果摸到的两个球都是红球,那么就中大奖。在有放回的3次摸球中,此人恰好两次中大奖的概率是多少?
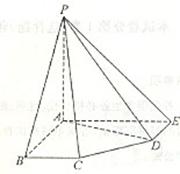 19、(本小题满分15分,第一小问满分5分,第二小问满分5分,第三小问满分5分)
19、(本小题满分15分,第一小问满分5分,第二小问满分5分,第三小问满分5分)
在五棱锥![]() 中,
中,![]() ,PB=PE
,PB=PE
![]() , BC=DE=
, BC=DE=![]() ,
,![]() 。
。
(I)求证:![]() 平面
平面![]() ;
;
(II)求二面角![]() 的大小。
的大小。
(III)求点C到平面PDE的距离。
20.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
在直角坐标系中,O为坐标原点,设直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]()
(I)求直线![]() 的方程;
的方程;
(II)如果一个椭圆经过点![]() ,且以点
,且以点![]() 为它的一个焦点,求椭圆的标准方程;
为它的一个焦点,求椭圆的标准方程;
(III)若在(I)、(II)、情形下,设直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,且
,且![]() ,当
,当![]() 最小时,求
最小时,求![]() 对应的值。
对应的值。
21、(本小题满分15分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
设不等式组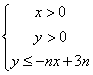 所表示的平面区域为Dn ,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n
所表示的平面区域为Dn ,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n![]() N*).
N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)记Tn=![]() ,若对于一切正整数n,总有Tn≤m,求实数m的取值范围;
,若对于一切正整数n,总有Tn≤m,求实数m的取值范围;
(3)设Sn为数列{bn}的前n项和,其中bn=![]() ,问是否存在正整数n、t,使
,问是否存在正整数n、t,使![]() 成立?若存在,求出正整数n , t;若不存在,说明理由.
成立?若存在,求出正整数n , t;若不存在,说明理由.
高三上第三次月考数学试卷参考答案
一选择题 ACADC CBCDB
二、填空题 11、1;12、(,);13、4;14、![]() ;15、6
;15、6![]() ;16、2。
;16、2。
三、解答题
17、
解(I)![]() 是等比数列,且
是等比数列,且![]() ,
, ![]()
![]() ………3分
………3分
![]()
![]() ……………………6分
……………………6分
(II)![]() 数列
数列![]() 是等差数列,
是等差数列,![]() ,
,
又![]()
![]()
![]()
![]()
![]()
从而![]() …9分
…9分 ![]()
![]()
![]()
![]() ……………………12分
……………………12分
18、解:(I)记“从袋中摸出的两个球中含有红球”为事件![]() 。则
。则
![]() (或“不含红球即摸出的两个球都是黑球”为事件
(或“不含红球即摸出的两个球都是黑球”为事件![]() 。
。
![]()
![]() ……5分 答:此人中奖的概率是
……5分 答:此人中奖的概率是![]() 。
。
(II)记“从袋中摸出的两个球都是红球”为事件B,则![]() …10分
…10分
由于有放回的3次摸球,每次是否摸到两个红球之间没有影响。
所以3次摸球恰好有两次中大奖相当于作用于次独立重复试验,根据![]() 次独立重复试验中事件恰好发生
次独立重复试验中事件恰好发生![]() 次的概率公式得,
次的概率公式得,![]() ……13分
……13分
答:此人恰好两次中大奖的概率是![]() ……………………………………14分
……………………………………14分
19、(I)证明:![]() ,
,![]()
![]()
![]() ,
,![]()
![]() 即
即![]() 同理
同理![]()
![]()
![]() 平面ABCDE………………5分
平面ABCDE………………5分
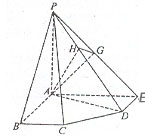 (II)解:
(II)解:![]() ,
,![]()
![]()
![]()
![]()
![]()
过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,![]()
![]() 平面
平面![]() 。
。
过![]() 作
作![]() 于H,连
于H,连![]() 由三垂线定理得
由三垂线定理得 ![]() 。
。 ![]()
![]() 为二面角
为二面角![]() 的平面角……………………8分
的平面角……………………8分
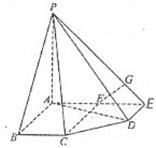 在
在![]() 中,
中,![]() 在
在![]() 中,
中,![]() ,
,![]() 在
在![]() 中,
中,![]() ,
,![]() 。
。![]() 二面角
二面角![]() 的大小为
的大小为![]() ………………10分
………………10分
(III)![]() ,
, ![]() ,
,
取![]() 中点
中点![]() ,连
,连![]() ,
,
![]()
![]() 四边形
四边形![]() 为平行四边形。
为平行四边形。
![]() 而
而![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 点
点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离。
的距离。
![]() 平面
平面![]()
![]()
又![]()
![]() ,
,![]() 平面PAE
平面PAE
![]() 平面
平面![]() 。
。 ![]() 。
。
![]() 的长即为
的长即为![]() 点到平面
点到平面![]() 的距离。…………………………13分
的距离。…………………………13分
在![]()
![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,
中点,![]()
![]()
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。……………………15分。
。……………………15分。
20、![]()
![]() 根据两点式得,所求直线
根据两点式得,所求直线![]() 的方程为
的方程为 ![]()
即 ![]() 。
。
![]() 直线
直线![]() 的方程是
的方程是![]() …………………………4分
…………………………4分
(II)解:设所求椭圆的标准方程为![]()
![]()
![]() 一个焦点为
一个焦点为![]()
![]() 即
即 ![]() ①…………6分
①…………6分
![]() 点
点![]() 在椭圆
在椭圆![]()
![]()
![]()
![]() 上,
上,
![]()
![]() ②
②
由①②解得 ![]()
所以所求椭圆的标准方程为 ![]() ………………………………9分
………………………………9分
(III)由题意得方程组
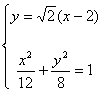 解得
解得 ![]() 或
或![]()
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 最小。…………………………………………14分
最小。…………………………………………14分
21、解(Ⅰ)由题意,作图易得f (1)=3,f (2)=6. ……………………2分
一般地,由![]() ,
,![]() ,得
,得![]() .
.
又![]() ,∴
,∴![]() .
.
∴Dn内的整点在直线![]() 和
和![]() 上. ……………………………………3分
上. ……………………………………3分
记直线![]() 为
为![]() ,
,![]() 与直线
与直线![]() 和
和![]() 的交点的纵坐标分别为
的交点的纵坐标分别为![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
∴![]() . ……………………………………………………5分
. ……………………………………………………5分
(Ⅱ)由(Ⅰ),得 ![]() , ……………………………………………6分
, ……………………………………………6分
∴![]() .
.
∴当n≥3时,![]() ,且
,且![]() .……………………………8分
.……………………………8分
于是![]() 是
是![]() 的最大项,故m≥
的最大项,故m≥![]() .…………………………………10分
.…………………………………10分
(Ⅲ)假设存在正整数n,t使得上面的不等式成立,
由(Ⅰ),有 ![]() ,∴
,∴ ![]() . ……………………………11分
. ……………………………11分
不等式![]() ,即
,即![]() ,
,
解得 ![]() .
.
∴n=t=1. ………………………………………………………………………14分
即存在正整数n=1,t=1,使![]() 成立. ………………………15分
成立. ………………………15分