高三上期第一学月考试试题数学试卷
（时间：120分钟 满分：150分）
说明：请把选择题和填空题做在答题卷上，只交答卷
一、选择题：（12×5=60分）
1、平面上有9个点，其中有4点共线，此外无3点共线，过其中任意两点作直线，不同的直线共（ ）
A．60条 B．61条 C．30条 D．31条
2、12.从单词“equation”中选取5个不同的字母排成一排，含有“qu”（其中“qu”相连且顺序不变）的不同的排列共有（ ）
A、120个 B、480个 C、720个 D、840个
3、五种不同的商品排成一排，要求其中
两件商品必须排在一起，
两种商品不能排在一起，那么不同的排法种数为（ ）
A. 12 B. 20 C. 24 D. 48
4、某办公室有8人，现从中选出3人参加A，B，C三项活动，其中甲不得参加A项活动，则不同的选派方法有（ ）
A．35种 B．56种 C．294种 D．336种
5、（理科做）若
的展开式中第5项的系数与第3项的系数之比是
，则展开式中的常数项是（ ）
A、0 B、45 C、90 D、180
5、（文科做）若
的展开式中只有第6项的系数最大，则常数项的值为（ ）
A．462 B．252 C． 10 D．210
6、一排九个坐位有六个人坐，若每个空位两边都坐有人，共有（ ）种不同的坐法
A．7200 B．3600 C．2400 D．1200
7、在(1+
x)7的展开式中,x3项的系数是x2项系数与x5项系数的等比中项,则的值为( )
A.
B.
C.
D.
8、在三张卡片的正反面上分别写有数字0与2，3与4，5与6，且6可以作9用，把这三张卡片拼在一起表示一个三位数，则三位数的个数为（ ）
A．12 B．72 C．60 D．40
9、如果(3x－
)n的展开式中各项系数之和为128,则展开式中
的系数是( )
A.7 B.-7 C.21 D.-21
10、
的展开式中，无理数项的个数是（ ）
A、84 B、85 C、86 D、87
11、
的展开式中，x的一次项的系数是（ ）
A．28 B．-28 C．56 D．-56
12、（理科做）若（2x＋
）4＝a0＋a1x＋a2x2＋a3x3＋a4 x4，则（a0＋a2＋a4）2－（a1＋a3）2的值为（ ）
A.1 B.－1 C.0 D.2
12、（文科做）若（2x＋
）4＝a0＋a1x＋a2x2＋a3x3＋a4 x4，则a0－a1＋a2－a3＋a4的值为（ ）
A.1 B.－1 C.0 D.2
二、填空题：（4×4＝16分）
13、由1,2,3,4,5组成比40000小的没有重复数字的五位偶数的个数是____________.（结果用数值表示）
14、在（1+x）6（1－x）4的展开式中，x3的系数是_____（结果用数值表示）.
15、8名世界网球顶级选手在上海大师赛上分成两组，每组各4人，分别进行单循环赛，每组决出前两名，再由每组的第一名与另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，大师赛共有____场比赛.
16、（理科做）设二项式
展开式的各项系数的和为P；二项式系数的和为S，且P+S=272，则展开式的常数项为_________．
16、（文科做））若（3x+1）n（n∈N*）的展开式中各项系数的和是256，则展开式中x2的系数是 .（结果用数值表示）
高三上期第一学月考试试题数学试卷
（时间：120分钟 满分：150分）
一、选择题：（12×5＝60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：（4×4＝16分）
13、 14、
15、 16、
三、解答题：（共74分，排列组合题结果均用数字作答）
17、（共12分）用数字0，1，2，3，4，5组成没有重复数字的数，
（1）能组成多少个是25的倍数的四位数；
（2）能组成多少个比240135大的数；
（3）若把所组成的全部六位数从小到大排列起来，第100个数是多少？
答案：（1）
；（2）
；（3）150342.
18、（共12分）在二项式
的展开式中：
（1）若第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项；
（2）若前三项的二项式系数和等于79，求展开式中系数最大的项。
答案：（1）
∴n=7或n=14，
当n＝7时，展开式中二项式系数最大的项是T4和T5，
且
；
当n＝14时，展开式中二项式系数最大的项是T8,，
且
（2）
∴n=12
设Tk+1项系数最大，
∴
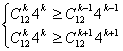∴9.4<k<10.4 ∴k=10
19、（共12分）一个口袋内有4个不同的红球，6个不同的白球。
（1）从中任取4个球，红球的个数不比白球少的取法有多少种？
（2）若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种？
20、（共12分）7名师生站在一排照相留恋，其中老师1名，男生4名，女生2名，在下列情况下，各有多少种不同的站法？
（1）、两名女生必须相邻而站；
（2）、4名男生互不相邻；
（3）、若4名男生身高都不相等，按从高到低的一种顺序站；
（4）、老师不站中间，女生不站两端；
21、（共12分）设f（x）是定义域在R上的一个给定的函数，函数g（x）＝
f（
）（1－ x）＋
f（
）x（1－x）n-1＋…＋
f（
）x n (1－x）（x≠0，1）
(1)当f（x）＝1时，求g（x）
（2）当f（x）＝x时，求g（x）
22．（共14分）设数列
是等比数列，
，公比
是(
)4的展开式中的第二项（按x的降幂排列）
（1） 用
表示通项
与前n项和
;
（2） （理科做，文科不做）若
，用表示
。