高三上学期月考试卷数学（文）试题（四）
时量：120分钟 满分：150分
一、选择题：本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．若x，a，2x，b成等比数列，则
的值为 （ ）
A．
B．
C．2 D．
2．若函数
= （ ）
A． B．－ C．－2 D．2
3．如果
那么必有 （ ）
A．
B．
|
D．
4．既是区间（0，
）上的增函数，又是以π为周期的偶函数的函数是 （ ）
A．y=sin2x（x∈R） B．y=sinx（x∈R）
C．y=cos2x（x∈R） D．y=esinx（x∈R）
5．等差数列{an}的首项a1=1，公差d≠0，如果a1，a2，a5成等比数列，那么d= （ ）
|
6．设x，y，z是空间不同的直线或平面，对于下列四种情形，使“x⊥z且y⊥z
x//y”为
真命题的是 （ ）
①x，y，z均为直线； ②x，y是直线，z是平面
③z是直线，x，y是平面； ④x，y，z均为平面.
A．①，② B．①，③ C．③，④ D．②，③
7．下列命题中错误的是 （ ）
A．命题“若q则p”与命题“若
p则q”互为逆否命题
B．“am2<bm2”是“a<b”的充要条件
C．“矩形的两条对角线相等”的否定为假
|
{1，2}或4
{1，2}”为真（其中为空集）
8．正方体ABCD—A1B1C1D1的侧面ABB1A1内有一动点P到直线AA1和BC的距离相等，
则动点P的轨迹是 （ ）
A．线段 B．抛物线的一部分 C．双曲线的一部分 D．椭圆的一部分
|
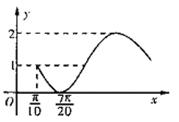
A．y=sin2x－2
B．y=2cos3x－1
C．y=sin(2x－
)+1
D．y=1－sin(2x－)
10．已知向量a=(m,n)，b=（cosθ，sinθ），其中m，n，θ∈R，若a=4b，则当a·b<λ2恒成立时，实数λ的取值范围是 （ ）
A．λ>或λ<－ B．λ>或λ<－2
C．－2<λ< D．－2<λ<2
二、填空题：本大题共52个小题，每小题4分，共20分.
11．先后抛掷两枚均匀的正方体骰子（它们的六个面分别标有1，2，3，4，5，6）骰子朝上的点数分别为x，y，则logxy=1的概率是 .
12．记Tn=a1·a2·…·an(n∈N*)表示n个数的积，其中ai为数列{an}中的第i项，若
an=2n－1,T4= .
13．若向量a,b是非零向量，则“a·b<0”是“向量a,b的夹角为钝角”的 条件.
14．函数
的单调递增区间是
.
15．顶点在原点，焦点在直线3x－4y－12=0上的抛物线的标准方程是 .
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.
16．（本小题满分12分）
设a=（
sinx，cosx），b=（cosx，cosx），若函数f(x)=a·b+m.（m∈R）
（Ⅰ）指出函数f(x)的最小正周期及单调递增区间；
（Ⅱ）当
时，函数f(x)的最小值为2，求此函数f(x)的最大值，并求此时的x
的值.
17．（本小题满分12分）
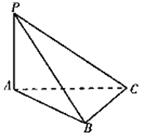
如图已知△ABC是正三角形，PA⊥面ABC，且PA=AB=a，
|
（Ⅱ）求二面A—PC—B的大小.
|
18．（本小题满分14分）
某人作短期旅游，上午7时出发，乘电动自行车以匀速v千米/小时(4≤v≤20)从甲地到距50千米的乙地，然后换乘汽车以u千米/小时（30≤u≤100）匀速的自乙地向距300千米的丙地驶去，在同一天的下午4到9时到达丙地，设汽车、电动自行车所需时间分别是x，y小时.
（Ⅰ）图示满足上述条件的x+y的范围
（Ⅱ）如果已知所需的经费z=100+3(5－x)+2(8－y)（元，那么v，u分别是多少时走得最经济？此时需经费多少元？
19．（本小题满分14分）
已知二次函数f(x)(x∈R)的二次项系数为正实数且满足f′(1)=0，
（Ⅰ）试判断函数f(x)的单调区间；
（Ⅱ）设向量a=(sinx，2)，b=(2sinx，)，c=（cos2x，1），d=（1，2）.求解不等式
f(a·b)>f(c·d).
20．（本小题满分14分）
设
有唯一解，已知
（Ⅰ）求函数的解析式；
（Ⅱ）求证：数列{
}是等差数列；
（Ⅲ）求数列{xn}的通项公式.
21．（本小题满分14分）
|
=1上一点（a>0，b>0）
已知
，
|
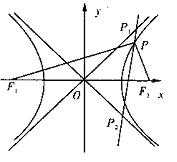
（Ⅱ）过点P作直线分别与双曲线的两条
渐近线相交于P1，P2两点，若
，
求双曲线C的方程.
参考答案
一、选择题：本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | C | B | A | D | B | B | D | B |
二、填空题：本大题共5个小题，每小题4分，共20分.
11．
12.105 13.必要不充分 14. 
15. x2=－12y或y2=16x
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.
16．解：（I）
f(x)的最小正周期是π，f(x)的单调递增区间是
…………………………………………………………（6分）
（II）
|
.……………………………………………………（12分）
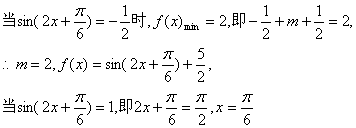
17．解：（I）在平面ABC作BC//AC，
且BE=AC连接AE，PE
则∠PBE是PB和AC所
成的角，∵PA⊥平面ABC，
△ABC为正三角形，PA=AB=a ,∴PE=a，
BE=a，在△PEB中，由余弦定理得
cos∠PBE=
……（6分）
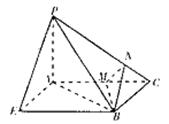
（II）取AC的中点M,连接BM，作MN⊥PC于N，连BN，
∵PA⊥平面ABC，
∴平面PAC⊥平面ABC，易证BM⊥AC.
∴BM⊥平面PAC，又MN⊥PC，
∴PC⊥BN，故∠MNB为二面角A—PC—B的平面角.
在Rt△BMN中，MN=CM·sin45°=
a BM=
a
∴tan∠BNM=
.
|
…………………………………………………………（12分）
18．解：（I）依题意得
∵4≤v≤20，30≤u≤100，3≤x≤10，
，又依题意知9≤x+y≤14
……………………（6分）
（II）由已知得3x+2y=131－z.
设131－z=m,则当m最大时，z最小.
在图示的满足不等式的平面区域（含边界）且斜率为
的直线3x+2y=m中，使m值最大的直线必通过点（10，4）.
即当x=10，y=4时，z最小，此时v=12.5，
u=30，z的最小值为93元.…………………………………………（14分）
19．解：（I）设
∴f(x)得单调递减区间为
，单调递半区间为
.………………（6分）
（II）依题意a·b=2sin2x+1≥1, c·d=cos2x+2=1+2cos2x≥1.
依题意f(a·b)>f(c·d)，
∴2sin2x+1>2cos2x+1sin2x>cos2xcos2x<0
…………………………………………（14分）
20．解：（I））因方程f(x)=x有唯一解，可求
………………（5分）
（II）
是公差为的等差数列；……（9分）
（III）数列{xn}的通项公式为
………………………………（14分）
21．解：（I）由
即△F1PF2为直角三角形，
因此有
…（6分）
（II）
依题意
①
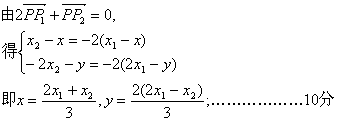
又因点在双曲线
将b2=4a2代入上式整理
②
由①·②得a2=2,b2=8，故求得双曲线方程为
.………………（14分）