高三数学三月(理)专题测试一
新增内容部分
一选择题
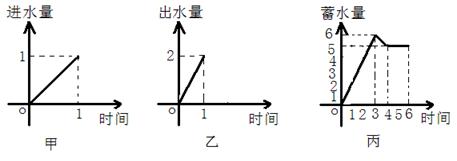
1.一水池有2个进水口,1 个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:
①0点到3点只进水不出水;②3点到4点不进水只出水;③ 4点到6点不进水不出水.则一定能确定正确的论断是( )
A.① B.①② C.①③ D.①②③
 2.甲、乙、丙、丁四位同学各自对
2.甲、乙、丙、丁四位同学各自对![]() 、
、![]() 两变量的线性相关性作试验,并用回归分析方法分别求得相关系数
两变量的线性相关性作试验,并用回归分析方法分别求得相关系数![]() 与残差平方和
与残差平方和![]() 如下表:(广东省韶关市高三摸底)
如下表:(广东省韶关市高三摸底)
| 甲 | 乙 | 丙 | 丁 | |
|
| 0.82 | 0.78 | 0.69 | 0.85 |
|
| 106 | 115 | 124 | 103 |
则哪位同学的试验结果体现![]() 、
、![]() 两变量更强的线性相关性?(
)
两变量更强的线性相关性?(
)
![]() 甲
甲
![]() 乙
乙
![]() 丙
丙 ![]() 丁
丁
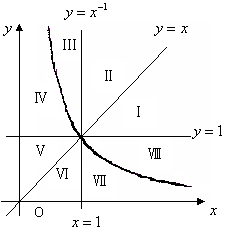 3.幂函数①
3.幂函数①![]() ,②
,②![]() 及直线③
及直线③![]() ,
,
④![]() 将直角坐标系第一象限分成八个“卦
将直角坐标系第一象限分成八个“卦
限”:Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ(如
图所示),那么幂函数![]() 的图象在第一象
的图象在第一象
限中经过的“卦限”是( )
A.Ⅳ,Ⅶ B. Ⅳ,Ⅷ C.Ⅲ,Ⅷ D. Ⅲ,Ⅶ
4.如图,在一根长11cm,外圆周长6cm的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为( )
![]() A.61cm
B.
A.61cm
B.![]() cm
cm
C.![]() cm
D.
cm
D.![]() cm
cm
5.已知命题![]() ,则
,则![]() 是( )
是( )
A.![]()
![]() B.
B.![]()
C.![]() D.
D.![]()
6.给出下面的程序框图,那么,输出的数是( )
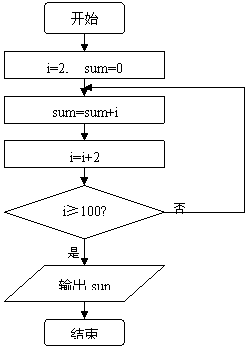

A.2450 B. 2550 C. 5050 D. 4900
7.某人睡午觉醒来,发现表停了,他打开收音机想听电台整点报时,则他等待时间小于10分钟的概率是( )
A ![]() B
B![]() C
C![]() D
D ![]()
8. “所有9的倍数(M)都是3的倍数(P),某奇数(S)是9的倍数(M),故该奇数(S)是3的倍数(P)”。上述推理是( )
A小前提错误 B大前提错误 C结论错误 D正确的
二填空题
9.![]()
![]() .
.
10.我们知道:“过圆为![]() 的圆外一点
的圆外一点![]() 作它的两条切线
作它的两条切线![]() 、
、![]() ,
,
其中![]() 、
、![]() 为切点,则
为切点,则![]() .”这个性质可以推广到所
.”这个性质可以推广到所
有圆锥曲线,请你写出其中一个:
.
11.已知n次多项式Pn(x)=a0xn + a1xn-1 + a2xn-2 +…+ an-1x + an ,如果在一种算法中,计算akx0k (k=2, 3, 4,…n)需要k次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算Pn(x0)的值共需要 次运算.(广州市顺德区)
下面给出一种减少运算次数的算法:P0(x)=a0 , Pk+1(x)=xPk(x) + ak+1 (k=0, 1, 2,…n-1), 利用该算法,计算P3(x0)的值共需要6次运算,那么计算Pn(x0)的值共需要 次运算.
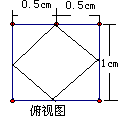
12.根据以下三视图想象物体原形,可得原几何体的体积是 。
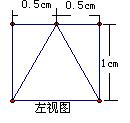
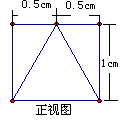
三解答题
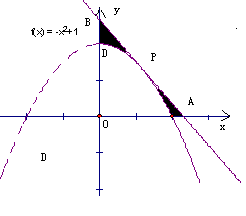
13.在抛物线![]() 上找一个点
上找一个点![]() 其中
其中![]() ,过点
,过点![]() 作抛物线的切线,使此切线与抛物线及连坐标轴所围平面图形的面积最小。
作抛物线的切线,使此切线与抛物线及连坐标轴所围平面图形的面积最小。
14. 某企业实行裁员增效,已知现有员工a人,每人每年可创纯利润1万元,据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的![]() ,设该企业裁员x人后纯收益为y万元.
,设该企业裁员x人后纯收益为y万元.
(1)写出y关于x的函数关系式,并指出x的取值范围;
(2)当140<a≤280时,问该企业应裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)
15.已知向量![]() ,规定
,规定![]() ,且
,且![]() 函数
函数![]() 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量![]()
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调区间;
的单调区间;
(3)是否存在正整数m,使得函数 ![]()
![]()
![]() (
(![]() )在区间(m,m+1)内有且只有两个不同零点?若存在,求出m的值;若不存在,说明理由.
)在区间(m,m+1)内有且只有两个不同零点?若存在,求出m的值;若不存在,说明理由.
16.设F1, F2分别为椭圆![]() 的左右两个交点.
的左右两个交点.
(1) 若椭圆C上的点![]() 到F1, F2两点的距离之和等于4, 写出椭圆C的方程和焦点坐标;
到F1, F2两点的距离之和等于4, 写出椭圆C的方程和焦点坐标;
(2)
设点K是(1)中所得椭圆上的动点,求线段![]() 的中点的轨迹方程;
的中点的轨迹方程;
(3)
已知椭圆具有性质: M,N是椭圆C上关于原点对称的两个点, 点P是椭圆上任意一点,当直线PM, PN的斜率都存在,并记为![]() ,
,![]() 时,那么
时,那么![]() 与
与![]() 之积是与点P位置无关的定值.试对双曲线
之积是与点P位置无关的定值.试对双曲线![]() 写出类似的性质,并给以证明.
写出类似的性质,并给以证明.
高三数学三月(理)专题测试一
一选择题ADDA,DAAD
二填空题
9. ![]()
10.①过抛物线![]() (
(![]() )外一点
)外一点![]() 作抛物线的两条切线
作抛物线的两条切线![]() 、
、![]() (
(![]() 、
、![]() 为切点),若
为切点),若![]() 为抛物线的焦点,则
为抛物线的焦点,则![]() .(如果学生写出的是抛物线的其它方程,只要正确就给满分)
.(如果学生写出的是抛物线的其它方程,只要正确就给满分)
②过椭圆![]() (
(![]() )外一点
)外一点![]() 作椭圆的两条切线
作椭圆的两条切线![]() 、
、![]() (
(![]() 、
、![]() 为切点),若
为切点),若![]() 为椭圆的一个焦点,则
为椭圆的一个焦点,则![]() .(如果学生写出的是椭圆的其它方程,只要正确就给满分)
.(如果学生写出的是椭圆的其它方程,只要正确就给满分)
③过双曲线![]() (
(![]() )外(两支之间)一点
)外(两支之间)一点![]() (
(![]() 不在渐近线上)作双曲线的两条切线
不在渐近线上)作双曲线的两条切线![]() 、
、![]() (
(![]() 、
、![]() 为切点),设
为切点),设![]() 为双曲线的一个焦点.⑴若
为双曲线的一个焦点.⑴若![]() 、
、![]() 在同一支,则
在同一支,则![]() ;⑵若
;⑵若![]() 、
、![]() 不在同一支,则
不在同一支,则![]() 平分
平分![]() 的邻补角.(如果学生写出的是双曲线的其它方程,只要正确就给满分)
的邻补角.(如果学生写出的是双曲线的其它方程,只要正确就给满分)
 11.
11. ![]() n(n+3),2n 12.
n(n+3),2n 12.![]()
![]()
三解答题
13.解:设过 ![]() 点的切线方程为
点的切线方程为![]() ,
,
由已知得![]() ,该直线与
,该直线与![]() 轴交点
轴交点![]() ,与
,与![]() 轴交点
轴交点![]()
![]()
=![]()
=![]() 利用导数可知当
利用导数可知当![]() 时
时![]() 最小
最小
![]() 当取切点
当取切点![]() 是所求图形面积最小。
是所求图形面积最小。
14. 解:(1)![]() …………2分
…………2分
![]() ,故x的取值范围
,故x的取值范围![]() …………4分
…………4分
(2)![]() …………………………6分
…………………………6分
当140<a≤280时,![]() 取最大值
取最大值
当a为奇数时,![]() ,y取最大值……………………10分
,y取最大值……………………10分
因尽可能少裁人![]()
∴当a为偶数时,应裁员![]() ,当a为奇数时,就裁员
,当a为奇数时,就裁员![]() ……………12分
……………12分
15.解:(1)由已知![]()
…………………………………………………………………1 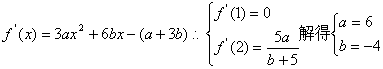 ………3′
………3′
![]() …………………………………………………4′
…………………………………………………4′
(2)![]()
由![]() >0得,
>0得,![]() 上单调递增。
上单调递增。
由![]() <0得,
<0得,![]() 上单调递减……………………8′
上单调递减……………………8′
(3)函数![]()
![]()
则![]()
当![]() 是单调减函数;
是单调减函数;
当![]() 是单调增函数……………………11′
是单调增函数……………………11′
![]()
∴函数g(x)在区间![]() 内分别 有唯一零点……………………13′
内分别 有唯一零点……………………13′
∴存在正整数m=1使得函数![]()
![]() 在区间(1,2)上有且只有两个不相等的零点。
在区间(1,2)上有且只有两个不相等的零点。
16.(1)椭圆C的方程为![]() ,焦点坐标
,焦点坐标![]() .
.
(2)所求轨迹方程为![]() .
.
(3)类似的性质为: 若M,N是双曲线![]() 上关于原点对称的两个点, 点P是椭圆上任意一点,当直线PM, PN的斜率都存在,并记为
上关于原点对称的两个点, 点P是椭圆上任意一点,当直线PM, PN的斜率都存在,并记为![]() ,
,![]() 时,那么
时,那么![]() 与
与![]() 之积是与点P位置无关的定值..
之积是与点P位置无关的定值..
证明:设点M的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,其中
,其中![]() .
.
又设点P的坐标为![]() ,
,
由 ![]() 得
得![]() ,
,
将 ![]() 代入得
代入得![]() .
.