高三数学上学期第二次月考试卷

　  

高三数学上学期第二次月考试卷

一、填空题：（4分×12＝48分）

1、函数y=sinx·cos(x+)+cosx·sin(x+)的周期是　　　　　　　　  。

2、设集合A＝｛5，log₂（x＋3）｝，B＝｛x，y｝，若A∩B＝｛2｝，则A∪B＝　　　　　　　　  。

3、设等比数列｛｝的公比为q＝，且，则＝　　　　　　  。

4、等差数列｛｝中，，则　　　　　　　　  。

5、已知P（－1，－5），向量＝｛2，3｝，若＝3，则Q的坐标　　　　　　　　  。

6、a∈R，若关于的方程至多有一个实根，则取值为　　　　　　　　  。

7、若,（n∈N）, 则=　 。

8、已知x∈(－,0)，cosx=，则　　　　　　　　  。

9、函数，x∈[1,a]，若它的最大值为，则实数的取值范围　　　　。

10、若直线与平行，则实数　　　　　 。

11、已知是定义在R上的奇函数，且，当x∈[0,1]时，，

则　　　　　　　　  。

12、数列｛｝是首项为，前n项和为的等差数列。将整理为后，可知点， 都在直线 上。类似的若｛｝是首项为，公比为的等比数列(q≠1)，则点在直线P₁(a₁,s₁), P₂(a₂,s₂),…, P_n(a_n,s_n)…

(n∈N)在直线　　　　　　　　　　  上。

二、 选择题（4分×4＝16分）

13、直线与的位置关系是（　　　 ）

A、相离　　　　　　　 B、相切　　　　　　 C、相交　　　　　 D、以上都可能

14、复数，，若，且，则（　　　 ）

A、1　　　　　　　　  B、　　　　　　 C、相交　　　　 D、

15、已知等比数列｛｝，公比q≠1，前n项和为，，则为（　　　 ）

A、｛0｝　　　　　　 B、｛0，1，｝　　　 C、｛1，｝　　　　 D、｛0，｝

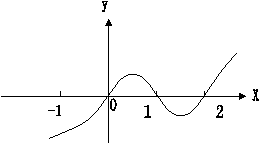16、已知函数的图像如图，

则的取值范围（　　　 ）

A、b∈(－∞,0)　　 B、b∈(0,1)　

C、b∈(1,2)　　　　D、b∈(2, ∞)

三、 解答题（86分，具体分值请看答案）

17、（12分）满足为实数，且的实部与虚部互为相反数的虚数是否存在？若存在，求；若不存在，说明理由。

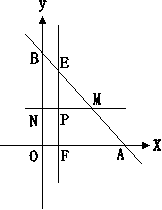18、（12分）如图，A，B，（），P为△AOB内一动点，过P作OA、OB的平行线分别交于E、F、M、N点，且△PEM与矩形OFPN面积始终相等。①求点P的轨迹。②当△PAB面积最大时，求P的坐标并求面积的最大值。

19、（14分）已知，·=，且(－)·(+)=

①求与的夹角　②若与λ+的夹角为，求实数λ的值

20、（14分）果厂生产A商品，若每件定80元，每年可销售80万件，税务部门对A商品征收附加税。本着既增加国家收入，又有利于市场繁荣，必须合理确立税率。据调查，若政府对A商品征收税率为P％（即每百元征P元）时，每年销售量减少10P万件，问

①若税务部门对A商品年收税金不少于96万元，求P的取值范围

②在所收税金不少于96万元的前提下，要让厂方有最大销售额，应如何确立P的值？

③若仅考虑每年收税金额最高，又如何确立P的值？

21、（16分）函数的定义域为A，的定义域为B　　  ① 求A ；　　② 若BA，求实数的范围

22、（18分）设函数f(x)=x－2+2(x≥2)，数列（），，当n≥2时，其前项之和，又有数列｛｝，，其前项之和为

① 求　　　　　　　 ② 求的解析式　　　　　 ③ 求的值.

高三数学第二次月考参考答案

一、填空题：（4分×12＝48分）

1. π  2. {1,2,5}　3. 　4. 0　5. (5,4)　 6.　a=0或a≥1　7. 　8.－　9.a≥3

10. 　11. 　12. y=

三、 选择题（4分×4＝16分）

13. B  14. C　15. B　16. A

三、解答题

17.解：设z=a+bi(a,b∈R,b≠0)　　　　　　　　　　　　　　　　　　 1′

　则a+bi+∈R,且a+b+3=0　　　　  　　　　　　　　　　　　3′

　化简得 b(a²+b²－5)²=0且a+b=3　　　　　　　　　　　　　　　　  6′

  ∴a=－1,b=－2或a=－2,b=－1　　　　　　　　　　　　　　　　  11′

　有虚数z=－1－2i或z=－2－i,满足题意　　　　　　　　　　　　  12′

18.解：(1)设P(x,y)(0<x<a,0<y<b)　　　　　　　　　　　　 　　　 1′

　 则F(x,0),N(0,y),E(x,a－x),M(a－y,y)　　　　　　　　　　　　 2′

　 由题意,xy=(a－x－y)(a－y－x)

　 整理得(x－a)²(y－a)²=a²,　　　　　　　　　　　　　　　　　　  5′

 ∴P的轨迹是以(a,b)为圆心,a为半径的圆在ΔAOB内的一段

 圆弧(不包含A,B二个点)　　　　　　　　　　　　 　　　　　　　 6′

 (2)当ΔPAB面积最大时,到AB的距离应最大为d.

  d=r－r=　　　　　　　　　　　　　　　　　　　　 8′

 S_ΔPAB最大值为··a=　　  　　　　　　　10′

 此时P(,)　　　　　　　　　　　　　　　　　 12′

19.解：(1)∵(－)(+)=1, ∴　　　　　 　　　　1′

　 ∵=1,　∴=1　　　　　　　　　　　　　　　　　　　　　  3′

　 cos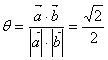　　　  ∴θ=45°　　　　　　　　　　　　 6′

　 (2) (－)²=,　　 ∴　　　　8′

　　 由题意 cos60°=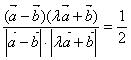　　　　　　　　　　　  9′

化简得,　　　　　　　　　　　　　　　　 12′

2

∴　　　　　　　　　　　  　　　　　　　　　 14′

20.解：(1)销售量：(80－10p)万件　　　　　　　　　　　　　　　　 1′

　　　　  销售额：80(80－10p)万件　　　　　　　　　　　　　　　 2′

　　　　  税金： 80(80－10p)·p%万件　　　　　　　　　　　　　  3′

　　　 由题意，96≤80(80－10p)·p%　　　　　　　　　　　　　  　4′

　　　 P²－8p+12≤0,　 ∴2≤p≤6　　　　　　　　　　　　　　　　 6′

　　 (2) 销售额：80(80－10p)　　 ∴f(2)_max=4800万元　　　　　　  10′

　　 (3) 税金：80(80－10p)·p%　　(0<p<8)

　　　　　　  =－8p²+64p=－8(p－4)²+128　　　　　　　　　　　　  12′

　　 ∴p=4时,税金最大为128万元　 　　　　　　　　　　　　　　　14′

21.解：(1)A：(－∞,－1)∪[1,+ ∞)　　　　　　　　　　　　　　　  4′

　　　 (2)(x－a－1)(x－2a)<0　　　　　　　　　　　　　　　　　　 5′

　　　 ∵2a≠a+1, ∴a≠1　　　　　　　　　　　　　　　　　　　　 6′

　　　 讨论：当a<1时, B=(2a,a+1)　　　　　　　　　　　　　　　　7′

　　　　∵BA,　 ∴2a≥1或a+1≤－1　　　　　　　　　　　　　　 9′

　　　　∴a≥或a≤－2　　　　　　　　　　　　　　 

　　　 又a<1,　　 ∴≤a<1或a≤－2　　　　　　　　　　　　 　11′

　　　　当a>1时, B=(a+1,2a)

　　　 ∵BA,　 ∴a+1≥1或2a≤－1　　　　　　　　　　　　　 

　　　 ∴a≥0或a≤－　　　　　　　　　　　　　　　　　　　　 13′

　　　 又a>1,　　 ∴a>1　　　　　　　　　　　　　　　　　　　　 15′

　　 当BA时,实数a的范围是(－∞,－2]∪[,1)∪(1,+ ∞)　　　 16′

22.解：(1)f^－1(x)=(+)² (x≥0)　　　　　　　　　　　　　　　 4′

　　　 (2)由题意 S_n=(+)²,得=+　　　　　　 6′

　　　 故{}是以为首项, 为公差的等差数列　8′

　　　∴=n　　　　　 S_N=2n²　　　　　　　　　　　　　　  10′

　　　　(3)由a_n=S_n－S_n－1=4n－2 (n≥2)

　　　∵a₁=2,　　　　∴a_n= 4n－2 (n∈N)　　　　　　　　　　　　  12′

　　　　　15′

　　　　 17′

　　　∴　 　　　　　　　　　　　　　18′