高三数学上学期月考（（理）试题四）
时量：120分钟 满分：150分
一、选择题：本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．如果
那么必有 （ ）
A．
B．
C．
D．
2．若函数
= （ ）
A．
B．－ C．－2 D．2
3．设x，y，z是空间不同的直线或平面，对于下列四种情形，使“x⊥z且y⊥z
x//y”为
真命题的是 （ ）
①x，y，z均为直线； ②x，y是直线，z是平面
③z是直线，x，y是平面； ④x，y，z均为平面.
A．①，② B．①，③ C．③，④ D．②，③
4．椭圆短轴长是2，长轴是短轴的2倍，则椭圆中心到其准线的距离是 （ ）
A．
B．
C．
D．
5．为了解湖中养鱼的多少，某人在湖中打了一网鱼，共m条，做上记号后放入湖中，数日
后又打了一网鱼，共n条，其中k条鱼有记号，估计湖中有鱼 （ ）
A．
条 B．
条 C．m
D．无法估计
6．正方体ABCD—A1B1C1D1的侧面ABB1A1内有一动点P到直线AA1和BC的距离相等，
则动点P的轨迹是 （ ）
A．线段 B．抛物线的一部分 C．双曲线的一部分 D．椭圆的一部分
7．定义运算
（ ）
A．奇函数 B．偶函数
C．既奇且偶函数 D．既非奇函数又非偶函数
8．椭圆
上有n(n∈N*)个不同的点：P1，P2，…，Pn，椭圆的右焦点为F，数列
{PnF}是公差不小于0.01的等差数列，则n的最大值是 （ ）
A．199 B．200 C．198 D．201
9．已知真命题：“a≥bc>d”和“a<be≤f”则“c≤d”是“e≤f”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既非充分条件也非必要条件
10．已知向量a=(m,n)，b=（cosθ，sinθ），其中m，n，θ∈R，若a=4b，则当a·b<λ2恒成立时，实数λ的取值范围是 （ ）
|
或λ<－ B．λ>或λ<－2
C．－2<λ< D．－2<λ<2
二、填空题：本大题共52个小题，每小题4分，共20分.
11．某人在黑暗中用6把钥匙随机开门，其中只有一把钥匙能把门打开，则在他在三次内（含3次）把门打开的概率是 .
12．记Tn=a1·a2·…·an(n∈N*)表示n个数的积，其中ai为数列{an}中的第i项，若
an=2n－1,T4= .
13．将一张坐标纸折叠一次，使得点（0，2）与点（－2，0）重合，且点（2005，2006）与点（m，n）重合，则n－m=
.
14．函数
的单调递增区间是 .
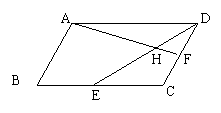
15．如图，在平行四边形ABCD中，E、F分别是BC、CD的中点，
DE与AF相交于点H, 设
等于 .
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.
16．（本小题满分12分）
设a=（
sinx，cosx），b=（cosx，cosx），若函数f(x)=a·b+m.（m∈R）
（Ⅰ）指出函数f(x)的最小正周期及单调递增区间；
（Ⅱ）当
时，函数f(x)的最小值为2，求此函数f(x)的最大值，并求此时的x的值.
17．（本小题满分12分）
如图，ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE和CE折起，使AE和BE重合，记A与B重合后的点为P，
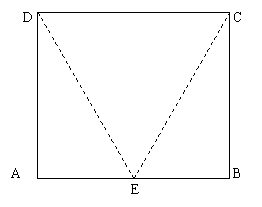（Ⅰ）求证：PE⊥面PCD；
（Ⅱ）求面PCD与面ECD所成的二面角的大小.
18．（本小题满分14分）
学校食堂定期向精英米业以每吨1500元的价格购买大米，每次购买大米需支付运输费用100元，已知食堂每天需食用大米1吨，储存大米的费用为每吨每天2元，假设食堂每次均在用完大米的当天购买.
（Ⅰ）问食堂每隔多少天购买一次大米，能使平均每天所支付的费用最少；
（Ⅱ）若购买量大，精英米业推出价格优惠措施，一次购买量不少于20吨时可享受九五折优惠，问食堂能否接受此优惠措施？请说明理由.
19．（本小题满分14分）
已知二次函数f(x)(x∈R)的二次项系数为正实数且满足f′(1)=0，
（Ⅰ）试判断函数f(x)的单调区间；
（Ⅱ）设向量a=(sinx，2)，b=(2sinx，)，c=（cos2x，1），d=（1，2）.求解不等式f(a·b)>f(c·d).
 |
20．（本小题满分14分）
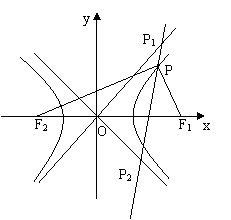
如图，P是以F1、F2为焦点的双曲线
C：
=1上一点（a>0，b>0）
已知
，
（Ⅰ）求双曲线的离心率；
（Ⅱ）过点P作直线分别与双曲线的两条渐近线相交于P1，P2两点，或
，求双曲线C的方程.
|
21．（本小题满分14分）
设
有唯一解，已知
（Ⅰ）求数列{xn}的通项公式；
（Ⅱ）若
，求和Sn=b1+b2+…+bn；
（Ⅲ）是否存在最小整数m，使得对任意n∈N*，有
成立，若存在，求出m的值，若不存在，说明理由.
参考答案
一、选择题：本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | D | B | B | B | A | D | A | B |
二、填空题：本大题共5个小题，每小题4分，共20分.
11．
12.105 13.1 14. 
15.
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.
16．解：（I）
f(x)的最小正周期是π，f(x)的单调递增区间是
…………………………………………………………（6分）
（II）
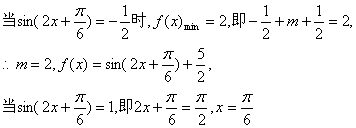
时f(x)取到最大值
.……………………………………………………（12分）
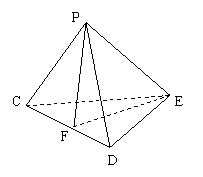17．解：（I）如图所示
∵P是A与B重合的点，且EA⊥AD，
（∠EAD=90°）EB⊥BC，
∴EP⊥PD，EP⊥PC，又PD与PC相交于P.
∴EP⊥平面PDC，…………………………（6分）
（II）取DC的中点F，连接EF、PF.
∵DE=CE，PD=PC，F是CD的中点.
∴PF⊥DC，EF⊥DC，从而∠PFE是二面角P—DC—E的平面角.
由（I）知EP⊥PF，设正方形ABCD的边长为a，则EP=，EF=a，
∴sin∠EFP=
,∴∠EFP=30°.
因此二面角P—CD—E为30°……………………………………………………（12分）
18．解：（I）设每隔t天购进大米一次，因为每天需林大米一吨，所以一次购大米t吨，那么库存费用为2[t+(t－1)+(t－2)+…+2+1]=t(t+1)，设每天所支出的总费用为v1，则
当且仅当t=
，即t=10时等号成立.
所以每隔10天购买大米一次使平均每天支付的费用最少.……………………（6分）
（II）若接受优惠条件，则至少每隔20天购买一次，设每隔n(n≥20)天购买一次，每天支付费用为y2，则y2=
+1426
上为增函数，
∴当n=20时，y2有最小值：
故食堂可接受
19．解：（I）设
∴f(x)得单调递减区间为
，单调递半区间为
.………………（6分）
（II）依题意a·b=2sin2x+1≥1, c·d=cos2x+2=1+2cos2x≥1.
依题意f(a·b)>f(c·d)，
∴2sin2x+1>2cos2x+1sin2x>cos2xcos2x<0
…………………………………………（14分）
20．解：（I）由
即△F1PF2为直角三角形，
因此有
…（6分）
（II）
依题意
①
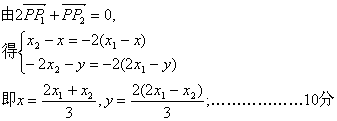
又因点在双曲线
将b2=4a2代入上式整理
②
由①·②得a2=2,b2=8，故求得双曲线方程为
.………………（14分）
21．解：（I）因方程f(x)=x有唯一解，可求a=从而得到
.
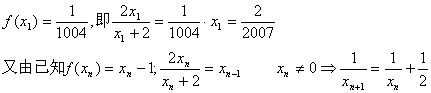
数列{
}是首项为
，公差为的等差数列，…………………………（4分）
故=
所以数列{xn}的通项公式为
………………（6分）
（II）将xn代入an可求得an=2n－1，所以
. 
…（10分）
（III）
恒成立，
即要
故存在最小的正整数m=3………（14分）