高三数学上学期周考试卷
（考试内容：函数与解几，考试时间120分钟，满分150分，命题人：张吉华）
一. 选择题（以下各题有且只有一个选项正确，每题5分，共60分）
1．映射f：A→B，如果满足集合B中的任意一个元素在Ａ中都有原象，则称为“满射”。已知集合A中有4个元素，集合B中有3个元素，那么从A到B的不同满射的个数为（ ）
A．24 B．6 C．72 D．36
2．若
则函数
的图象关于（ ）
A．直线y=x对称 B．x轴对称 C． y轴对称 D．原点对称
3．已知θ∈R，则直线
的倾斜角的取值范围是（ ）
A．[0°，30°] B．[0°，30°]∪
C． D．[30°，150°]
4．若P（4，－9），Q（－2，3），则直线PQ与y轴的交点分
所成的比为（ ）
A．
B．
C．2
D．3
5．已知实数x，y满足
的最小值为（ ）
A．
B．
C．2 D．2
6．设函数
+ b+ c 给出下列四个命题：①c = 0时，y是奇函数②b0 , c >0时，方程0 只有一个实根
③y的图象关于(0 , c)对称
④方程0至多两个实根，其中正确的命题是（ ）
A．①、④ B．①、③ C．①、②、③ D．①、②、④
7．若关于
的方程
有且只有两个不同的实数根，则实数
的取值范围是（ ）A．
B．
C．
D．
8．双曲线
的渐近线方程是（ ）
A．
B．
C．
D．
9．抛物线
中，F是焦点，P是其上动点，则线段PF中点的轨迹方程是（ ）
A．
B．
C．
D．
10．共焦点的椭圆
(a>b>0)和双曲线
(m,n>0)的交点是P，则PF1PF2为（ ）A．
B．
C．
D．
11．下列结论， ①渐近线方程为
的双曲线标准方程必是
；②抛物线
的准线方程是
；③等轴双曲线的离心率是
；④椭圆
焦点坐标是
其中正确的是（ ）
A．①② B．②③ C．③ D．③④
12．若a
b，且a
sin
+acos－
=0 ，bsin+bcos－
=0，则过（a，a），（b，b）两点的直线与单位圆的位置关系是（ ）
A．相交 B．相切 C．相离 D．不能确定
二．填空题（每题4分，不给中间分，共12分）
13．已知x、y满足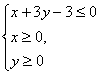
，则z＝
的取值范围是
14．过直线
上一点M向圆
作切线，则M到切点的最小距离为
_ ____
15．有一系列椭圆，满足条件：①中心在原点；②以直线x=2为准线；③离心率
，则所有这些椭圆的长轴长之和为
16．已知曲线
与其关于点(1,1)对称的曲线有两个不同的交点A和B，如果过这两个交点的直线的倾斜角是
，则实数a的值是_____________
高三数学上学期周考试卷
（考试内容：函数与解几，考试时间120分钟，满分150分，命题人：张吉华）
| 题号 | 一 | 二 | 17 | 18 | 19 | 20 | 21 | 22 | 成绩 |
| 得分 |
一. 选择题（每题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二. 填空题（每题4分，不给中间分，共12分）
13． 14．
15． 16．
三. 解答题（共74分）
17．在平面直角坐标系中，在y轴的正半轴上给定A、B两点，在x轴正半轴上求一点C，使∠ACB取得最大值．
18．(12分) 已知函数f(x)=ax2-2x+2 (a>0)，当x∈[1，4]时，f(x)>0恒成立，求实数a的取值范围．
19．（12分）已知圆(x+4)2+y2=25的圆心为M1，圆(x－4)2+y2=1的圆心为M2，一动圆与这两个圆都外切.
（1）求动圆圆心P的轨迹方程；
（2）若过点M2的直线与（1）中所求轨迹有两个交点A、B，求AM1·BM1的取值范围.
20．（12分）已知抛物线
的一条焦点弦被焦点分成长为m、n的两部分. 求证：
为定值。
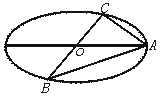
21．（12分）已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个顶点，BC过椭圆中心O，如图，且
·
=0，BC=2AC，
（1）求椭圆的方程；
（2）如果椭圆上两点P、Q，使∠PCQ的平分线垂直AO，则是否存在实数λ,使
=λ
？请说明理由..
22．（14分）如图所示，已知圆
为圆上一动点，点P在AM上，点N在CM上，且满足
轨迹为曲线E.
（1）求曲线E的方程；
|
，求
的取值范围.