高三数学文科第二学期第一次模拟考试
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分，考试时间120分钟。
参考公式：
如果事件A、B互斥，那么
P（A+B）=P（A）+P（B）
球的表面积公式
如果事件A、B相互独立，那么
P（A·B）=P（A）·P（B） 其中R表示球的半径
如果事件A在一次试验中发生的概率是
球的体积公式
P，那么n次独立重复试验中恰好发生k次的概率 ： 其中R表示球的半径
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中。有且只有一项符合题目要求。
1．设
A．R B．M C．N D．
2．函数
的反函数是
A．
B．
C．
D．
3．设
A．17 B．－17 C．－1 D． 1
4．双曲线
上的点到两条渐近线距离的乘积为
A．
B．a C．
D．a2
5．等差数列
的前n项和为Sn，若（
）（
）<0，则
A．
B．
C．
D．
=0
6．半径为R的球面上三点A、B、C，它们任意两点之间的球面距离都等于
，则球心到
平面ABC的距离为
A．
B．
C．
D．R
7．过点P作y轴的垂线，垂足为M，设
，且线段MN的垂直平分线过点P，
则动点P的轨迹是
A．圆 B．椭圆 C．双曲线 D．抛物线
8．设A、B是锐角三角形的两个内角，则直线
的倾斜角
A．大于135° B．大于90°且小于135°
C．大于45°且小于90° D．小于45°
9．已知p：关于x的不等式
的解集为R：q；关于x的不等式
的解集为R，则p成立是q成立的
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．即不充分也不必要条件
10．若
A．
B．
C．
D．
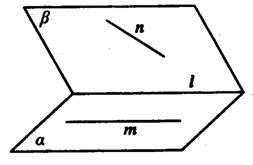
11．m、n是异面直线，m⊥平面
，n⊥平面
，l是直线
①若m⊥n，则⊥
②若m⊥l，n⊥l，则l//，或l//
③与不可能平行；
④若⊥，且l//，l//，则l是m、n的公垂线.
A．①③ B．②④ C．①④ D．②③
12．在6张卡片上分别写有1，2，3，4，5，6，将它们排成一排，得到能被4整除的6位数共有
A．144个 B．120个 C．192个 D．168个
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分
13．
的展开式中
的系数是21，则
的系数为
.
14．设x、y满足
的最大值为
.
|
|
是60°的二面角，直
线
m与n成60°
的角，则n与所成的角为
.
16．①若a>b>c>d，则ac>bd；
②
上递减；
③若三次函数
是奇函数，则其图象与x轴不可能有两个公共点；
④函数
.
其中真命题的序号是 .（把所有真命题的序号都填上）
三、解答题：本大题共6小题，共74分，解答 应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）已知函数
的图象过点
|
.
（Ⅰ）求实数a的值；
（Ⅱ）求函数
的最小值及相应自变量x的取值集合.
18．（本小题满分12分）两个排球队进行比赛采用五局三胜的规则，即先胜三局的队获胜，比赛到此也就结束，假设原定队员组合，较强队每局取胜的概率为0.6，若前四局出现2比2的平局情况，较强队按就换人重新组合队员，则其在决赛局中获胜的概率为0.7.
（Ⅰ）求三局结束比赛的概率；
（Ⅱ）求五局结束比赛的概率.
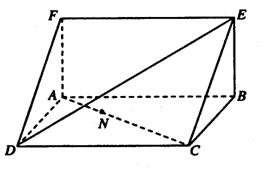
19．（本小题满分12分）如图面积为6的正方形ABCD所在平面与面积为
的短形ABEF所在平面互相垂直，点A在平面CDE上的射影为M，N∈AC，且NC=2AN.
|
（Ⅱ）证明：MN//平面ABEF.
|
20．（本小题满分12分）定义在R上的函数
（Ⅰ）当a=1时，求函数在[－1，1]上的最大值；
（Ⅱ）求函数的单调区间.
21．（本小题满分12分）已知数列的前n项和Sn满足
，数列
…是等比数列.
（Ⅰ）求数列的通项公式；
（Ⅱ）求数列
的通项公式；
22．（本小题满分14分）已知椭圆
是椭圆上纵坐标不为零的两点，若
其中F为椭圆的左焦点.
（Ⅰ）求椭圆的方程；
（Ⅱ）求线段AB的垂直平分线在y轴上的截距的取值范围.
参考答案
一、选择题
BBBDA ADCBC AC
二、填空题
13．35
14．4
15．
16．③④
三、解答题
17．解：
（Ⅰ）
由已知，得
∴a=1……………………………………4分
（Ⅱ）
……………………………………6分
设曲线
处的切线斜率为k，
则
……………………………………8分
当
时，k取最大值2. ………………10分
此时，
……12分
18．解：
（Ⅰ）三局结束比赛的概率
…………………………6分
（Ⅱ）五局结束比赛的概率
……………12分
19．解：
（Ⅰ）∵DC//AB，AB//EF，
∴DC//EF，因此C、D、F、E共面.
由已知，AB⊥AF，AB⊥AD，则AB平面⊥ADF.
∵CD//AB，
∴CD⊥平面ADF，
∴平面CDE⊥平面ADF，且交线为DF.
于是M∈DF，∠MCA为AC与平面CDE所成的角. ……………………………4分
∵平面ABCD⊥平面ABEF，
∴∠DAF=90°.
由已知，AD=
，得DF=3，AM=
，又AC=
，
|
故AC与平面CDE所成的角为
…………8分
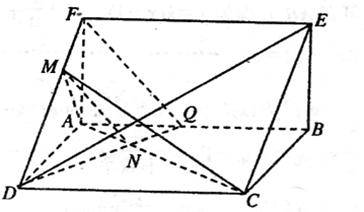
（Ⅱ）连结DN并延长交AB于Q，连结FQ.
由（Ⅰ）可得MF=1，MD=2，又△CDN∽△AQN,
∴
∴
∴MN//QF，
而MN
平面ABEF，QF
平面ABEF，
∴MF//平面ABEF. ……………………………………12分
20．解：
（Ⅰ）当a=1时，
…………………………2分
当
上单调递增.
故当
………………5分
（Ⅱ）
当
单调递增；
当
在（－
，2）和（2，+）分别单调递增.
由函数的连续性，知
单调递增. …………………………7分
当
当
单调递增；
当
单调递减. …………………………10分
综上，
当
的单调递增区间是（－，+）；
当
单调递减区间是
21．解：
（Ⅰ）
两式相减，得
.…………………………12分
当n=1时，
显然成立，
所以数列的通项公是为
…………………………4分
（Ⅱ）因为
，所以…的公比为4，所以
.
……………………………………6分
由等比数列的通项公式得
……………………8分
由等差数列的通项公式得
……………………10分
所以
……………………………………12分
22．解：
（Ⅰ）由已知，得
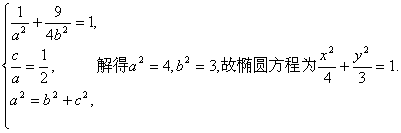………4分
（Ⅱ）∵A、B是椭圆上纵坐标不为零的点，
∴A、F、B三点共线，且直线AB的斜率存在且不为0.
又F（－1，0），则可记AB方程为
并整理得
……………………………………7分
显然△>0，设
……………………9分
直线AB的垂直平分线方程为
令x=0，得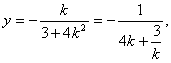
……………………………………12分
∵
“=”号，
∴
，
所以所求的取值范围是
……………………………………14分