高三数学第一轮复习单元测试
圆维曲线
一.选择题:
1.若双曲线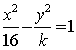 的一条准线恰好为圆
的一条准线恰好为圆![]() 的一条切线,则实数
的一条切线,则实数![]() 的值为
( )
的值为
( )
A.48 B.42 C.64 D.16
2. 椭圆短轴的一个端点看长轴两端点的视角为![]() ,则这个椭圆的离心率是( )
,则这个椭圆的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 设双曲线以椭圆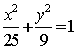 的长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为
( )
的长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.抛物线![]() 上一点
上一点![]() 到焦点的距离为1,则点
到焦点的距离为1,则点![]() 的纵坐标是
( )
的纵坐标是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.0
D.0
5.(理)已知双曲线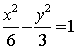 的焦点为
的焦点为![]() ,点
,点![]() 在双曲线上且
在双曲线上且![]() 轴,则
轴,则![]() 到直线
到直线![]() 的距离为
( )
的距离为
( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
(文)双曲线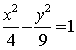 的渐近线的方程是
( )
的渐近线的方程是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 若椭圆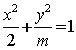 的离心率为,则
的离心率为,则![]() =
( )
=
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
7.过点(0,1)与双曲线![]() 仅有一个公共点的直线共有 ( )
仅有一个公共点的直线共有 ( )
A.1条 B.2条 C.3条 D.4条
8. 已知点A(0,1)是椭圆![]() 上的一点,P点是椭圆上的动点,则弦AP长度的最大值为
( )
上的一点,P点是椭圆上的动点,则弦AP长度的最大值为
( )
A. 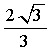 B.
B. 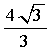 C.2
D.4
C.2
D.4
9.已知双曲线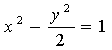 的焦点为
的焦点为![]() ,点M在双曲线上,且
,点M在双曲线上,且![]() ,则点M到
,则点M到![]() 轴的距离为
(
)
轴的距离为
(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.(理)过抛物线![]() 的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线
(
)
的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线
(
)
A.有且只有一条 B.有且人仅有两条 C.有无穷多条 D.不存在
(文)过抛物线![]() 的焦作一条直线与抛物线相交于A、B两点,且
的焦作一条直线与抛物线相交于A、B两点,且![]() ,则这样的直线有
( )
,则这样的直线有
( )
A.一条 B.两条 C.三条 D.不存在
11.(理)已知![]() 是双曲线
是双曲线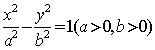 的两焦点,以线段
的两焦点,以线段![]() 为边作正三角形
为边作正三角形![]() ,若
,若![]() 的中点在双曲线上,则双曲线的离心率为 ( )
的中点在双曲线上,则双曲线的离心率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(文)已知定点A、B,且![]() ,动点P满足
,动点P满足![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.5
D.5
12.若动点![]() 在曲线
在曲线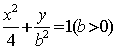 上变化,则
上变化,则![]() 的最大值为 ( )
的最大值为 ( )
A. ![]() B.
B. ![]() C.
C. 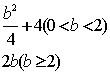 D.
D. 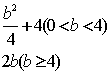
二、填空题
13.过双曲线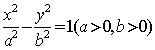 的左焦点,且垂直于
的左焦点,且垂直于![]() 轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于
。
轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于
。
14. ![]() 是双曲线
是双曲线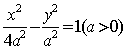 的两个焦点,P为双曲线上一点,
的两个焦点,P为双曲线上一点,![]() ,且
,且![]() 的面积为1,则
的面积为1,则![]() 的值是 。
的值是 。
15.点P在椭圆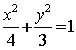 上运动,Q、R分别在两圆
上运动,Q、R分别在两圆![]() 和
和![]() 上运动,则
上运动,则![]() 的最大值为
;最小值为
。
的最大值为
;最小值为
。
16.(理)连结抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号)。①菱形 ②有3条边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形;
(文)已知![]() 是圆
是圆![]() (F为圆心)上一动点,线段AB的垂直平分线交BF于点P,则动点P的轨迹方程是
。
(F为圆心)上一动点,线段AB的垂直平分线交BF于点P,则动点P的轨迹方程是
。
三、解答题:
17.已知点A(0,1)及圆![]() ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
18.在抛物线![]() 上恒有两点关于直线
上恒有两点关于直线![]() 对称,求
对称,求![]() 的取值范围。
的取值范围。
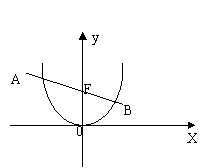 19.如图所示,已知一次函数
19.如图所示,已知一次函数![]() 与二次函数
与二次函数![]() 相交于
相交于![]() ,
,![]() ,两点,其中
,两点,其中![]() ,且
,且![]() :
:
①求![]() 的值
的值
②求![]() 关于
关于![]() 的函数关系式
的函数关系式
③当![]() 时,求以原点为中心,下为一个焦点且过点B的椭圆方程。
时,求以原点为中心,下为一个焦点且过点B的椭圆方程。
20.已知定点![]() ,动点P满足
,动点P满足![]()
(1)求动点P的轨迹方程,并说明轨迹的形状;
(2)当![]() 时,求
时,求![]() 的取值范围。
的取值范围。
21.(理)已知椭圆![]() 的方程为
的方程为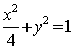 ,双曲线
,双曲线![]() 的左、右焦点分别是
的左、右焦点分别是![]() 的左、右顶点,而
的左、右顶点,而![]() 的左、右顶点分别是
的左、右顶点分别是![]() 的左、右焦点。
的左、右焦点。
(1)求双曲线![]() 的方程;
的方程;
(2)若直线与椭圆![]() 及双曲线
及双曲线![]() 都恒有两个不同的交点,且
都恒有两个不同的交点,且![]() 与
与![]() 的两个交点,A和B满足
的两个交点,A和B满足![]() (其中O为原点),求
(其中O为原点),求![]() 的范围。
的范围。
(文)已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(![]() )。
)。
(1)求双曲线C的方程;
(2)若直线![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且![]() (其中O为原点)求
(其中O为原点)求![]() 的范围。
的范围。
22.(理)如图,设抛物线![]() 的焦点为F,动点P在直线
的焦点为F,动点P在直线![]() 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别切于A、B两点。
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别切于A、B两点。
(1)求![]() 的重心G的轨迹方程。
的重心G的轨迹方程。
(2)证明![]()
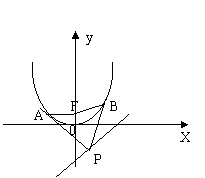
 (文)如图,
(文)如图,![]() 是抛物线
是抛物线![]() 上的一点,动弦ME、MF分别交力轴于A、B两点,且MA=MB。
上的一点,动弦ME、MF分别交力轴于A、B两点,且MA=MB。
(1)若M为定点,证明直线EF的斜率为定值。
(2)若M为动点,且![]() ,求
,求![]() 的重心G的轨迹方程。
的重心G的轨迹方程。
圆锥曲线 参考答案
一、选择题:
1.A 2.D 3.C 4.B 5.C 6.D 7.D 8.B 9.C 10.B 11.(理)D (文)C 12.D
二、填空题:
13. 2
14. 1
15. 6,2 16.(理)②③⑤(文)![]()
三、解答题:
17.连AP,![]() 垂直平分AC,
垂直平分AC,![]()
![]() ,即点P的轨迹是以A、B为焦点的椭圆,
,即点P的轨迹是以A、B为焦点的椭圆,
又![]()
![]() 点P的轨迹方程为
点P的轨迹方程为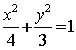 。
。
18.设![]() 关于直线
关于直线![]() 对称,直线BC的方程为
对称,直线BC的方程为![]() ,代入
,代入![]() ,得
,得![]()
设BC的中点M为![]() ,则
,则![]()
![]() 点
点![]() 在直线
在直线![]() 上,
上,![]() ,
,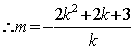
又直线BC与抛物线交于不同的两点,![]()
将![]() 代入,化简得
代入,化简得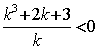 ,即
,即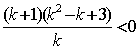
解得![]() 。
。
19.(1)由 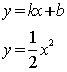
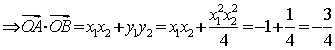
(2)![]()
又由![]() 得
得![]()
(3)当![]() 时,
时,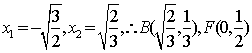
设椭圆的方程为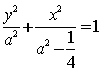 且过点B
且过点B
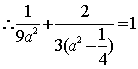 ,即
,即![]() 或
或![]()
又![]() ,故
,故![]() ,所以所求为
,所以所求为![]() 。
。
20.(1)设动点![]() ,则
,则![]() ,
,
![]()
![]() ,整理得:
,整理得:
![]()
若![]() ,方程为
,方程为![]() ,表示过点
,表示过点![]() 平行于
平行于![]() 轴的直线,
轴的直线,
若![]() ,方程为
,方程为![]() ,表示以
,表示以![]() 为圆心,以
为圆心,以![]() 为半径的圆。
为半径的圆。
(2)当![]() 时,方程化为
时,方程化为![]() ,
,
![]()
又![]() 的范围为
的范围为![]() 。
。
21.(理)(1)设双曲线![]() 的方程为
的方程为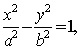 则
则![]()
再由![]() 得
得![]() ,故
,故![]() 的方程为
的方程为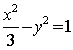
(2)将![]() 代入得
代入得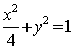 ,得
,得
![]() ,由直线
,由直线![]() 与
与![]() 恒有两个不同的交点,得:
恒有两个不同的交点,得:
![]() ,即
,即![]() ①
①
将![]() 代入
代入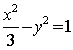 ,得
,得
![]() ,由直线
,由直线![]() 与
与![]() 恒有两个不同的交点,得:
恒有两个不同的交点,得:
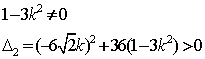
即![]() 且
且![]() ②
②
设![]() ,则
,则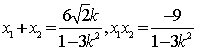
由![]() 得
得![]() ,而
,而
![]()
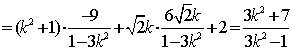 ,
,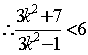
即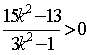 ,解得
,解得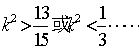 ③
③
由①、②、③得: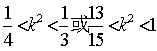
故K的取值范围为: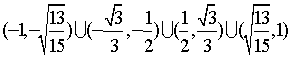 。
。
(文)(1)设双曲线方程为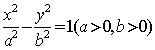
由已知得![]()
故双曲线C的方程为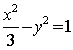
(2)将![]() 代入
代入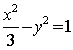 得
得![]()
由直线![]() 与双曲线交于不同的两点得:
与双曲线交于不同的两点得:
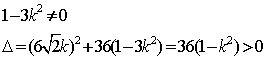
![]() 且
且![]() ①
①
设![]() ,则
,则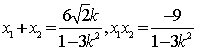
![]()
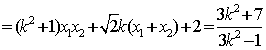
又![]() ,得
,得![]()
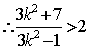
即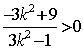 ,解得:
,解得:![]() ②
②
由①、②得:![]()
故K的取值范围为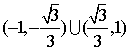 。
。
22.(理)(1)设切点A、B坐标分别为![]() 和
和![]()
![]() 切线AP的方程为:
切线AP的方程为:![]()
切线BP的方程为:![]()
解得点P的坐标为:![]()
![]() 的重心G的坐标为:
的重心G的坐标为:
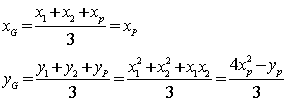
由点P在![]() 上运动,从而得到重心G的轨迹方程为:
上运动,从而得到重心G的轨迹方程为:
![]() ,即
,即![]()
(2)因为![]()
由于点P在抛物线外,则![]()
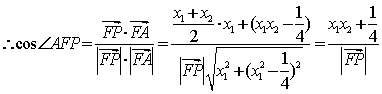
同理,有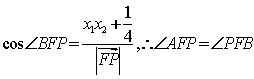 。
。
(文)(1)设![]() ,直线ME的斜率为
,直线ME的斜率为![]() ,则直线MF的斜率为
,则直线MF的斜率为![]() 。
。![]() 直线ME的方程为:
直线ME的方程为:![]()
由 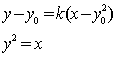 消
消![]() 得:
得:![]()
解得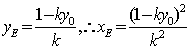
同理得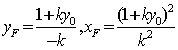
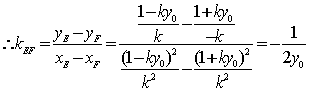 (定值)
(定值)
所以直线EF的斜率为定值。
(2)当![]() 时,
时,![]() ,所以
,所以![]()
![]() 直线ME的方程为:
直线ME的方程为:![]()
由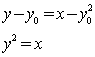 ,得
,得![]()
同理可得![]()
设重心![]() ,则有
,则有
![]()
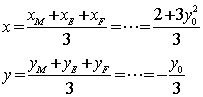 消去
消去![]() 得
得![]()