高三数学第一学期期末复习练习卷(1)
班级 姓名 座号
一、选择题(共10小题,每题5分)
1.已知复数![]() ,
,![]() ,则在
,则在![]() 复平面上对应的点位于(
)
复平面上对应的点位于(
)
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
2.有3张奖券,其中2张可中奖,现3个人按顺序依次从中抽一张,小明最后抽,则他抽到中奖券的概率是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.已知命题![]() ,命题
,命题![]() 的解集是
的解集是![]() ,下列结论:
,下列结论:
①命题“![]() ”是真命题; ②命题“
”是真命题; ②命题“![]() ”是假命题;
”是假命题;
③命题“![]() ”是真命题; ④命题“
”是真命题; ④命题“![]() ”是假命题
”是假命题
其中正确的是( )
(A)②③ (B)①②④ (C)①③④ (D)①②③④
4.已知![]() ,则
,则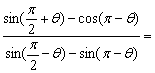 ( )
( )
(A)2 (B)-2 (C)0 (D)![]()
5.![]() 有解的区域是( )
有解的区域是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.已知向量![]() ,
,![]() ,若向量
,若向量![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2
7.已知两点![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,则
上任意一点,则![]() 面积的最小值是( )
面积的最小值是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8. 甲、乙、丙、丁四位同学各自对![]() 、
、![]() 两变量的线性相关性作试验,并用回归分析方法分别求得相关系数
两变量的线性相关性作试验,并用回归分析方法分别求得相关系数![]() 与残差平方和
与残差平方和![]() 如下表:
如下表:
| 甲 | 乙 | 丙 | 丁 | |
|
| 0.82 | 0.78 | 0.69 | 0.85 |
|
| 115 | 106 | 124 | 103 |
则哪位同学的试验结果体现![]() 、
、![]() 两变量更强的线性相关性?( )
两变量更强的线性相关性?( )
![]() 甲
甲
![]() 乙
乙
![]() 丙 (D) 丁
丙 (D) 丁
 9.如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为(
)
9.如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为(
)
(A)1 (B)![]()
(C)![]() (D)
(D)![]()
10.已知抛物线![]() ,过点
,过点![]() )作倾斜角为
)作倾斜角为![]() 的直线
的直线![]() ,若
,若![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,弦
两点,弦![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,则线段
,则线段![]() 的长为(
)
的长为(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(共4小题,每小题5分)
11.已知圆C的方程是![]() ,它关于极轴对称的圆的方程为 ;它关于直线
,它关于极轴对称的圆的方程为 ;它关于直线![]() 对称的圆的方程为
.
对称的圆的方程为
. ![]()
12.在约束条件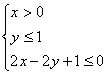 下,目标函数
下,目标函数![]() 的最大值为______2______.
的最大值为______2______.
13.在![]() 中,若
中,若![]() ,则
,则![]() 的外接圆半径
的外接圆半径![]() ,将此结论拓展到空间,可得出的正确结论是:在四面体
,将此结论拓展到空间,可得出的正确结论是:在四面体![]() 中,若
中,若![]() 两两垂直,
两两垂直,![]() ,则四面体
,则四面体![]() 的外接球半径
的外接球半径![]() _____
_____![]() _______.
_______.
14.在如下程序框图中,输入![]() ,则输出的是_
,则输出的是_ ![]() _________.
_________.
![]()

三、解答题
15、已知![]() 。
。
(1)化简![]() 的解析式;
的解析式;
(2)若0![]() ,求
,求![]() 使函数
使函数![]() 为偶函数。
为偶函数。
(3)在(2)成立的条件下,求满足![]() =1,
=1,![]() [
[![]() ]的
]的![]() 的集合。
的集合。
解:(1)![]()
=![]()
(2)![]()
![]() 当
当![]() 时,
时,![]() =
=![]() 此时,
此时,![]() 为偶函数.
为偶函数.
(3)由(2)可知![]() =
=![]() 当
当![]() =1,即
=1,即![]() =1得
=1得![]() ,
,
则 ![]()
![]()
∵![]() ∴
∴![]()
![]()
∴![]() 的集合为
的集合为![]()
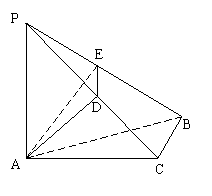 16、如图,三棱锥P-ABC中,
16、如图,三棱锥P-ABC中,![]() ACB=90
ACB=90![]() ,PA面ABC,AD
,PA面ABC,AD![]() PC,AE
PC,AE![]() PB.D、E为垂足.
PB.D、E为垂足.
(1)证明:PB![]() 平面ADE;
平面ADE;
(2)若PA=AB=2,求三棱锥P-ADE体积的最大值。
(1)证明:∵AC⊥BC,PA⊥BC ∴BC⊥面PAC
∴BC⊥AD又∵AD⊥PC ∴AD⊥面PCB
∴AD⊥PB 又∵AE⊥PB ∴PB⊥面ADE 。
(2)解:∵PA=AB=2,AE⊥PB,PA⊥面ABC
∴PE=AE=![]() ∴VP-ADE=
∴VP-ADE=![]() S⊿ADE ·PE
S⊿ADE ·PE
=![]()
![]()
![]() AD·DE·
AD·DE·![]() =
=![]() ·AD·DE
·AD·DE![]()
![]() (AD2·DE2)=
(AD2·DE2)=![]() AE2=
AE2=![]()
∴VP-ADE的最大值为![]() 此时AD=DE=
此时AD=DE=![]() AE=1 ,AC=
AE=1 ,AC=![]() <2
<2
17、已知![]() =
=![]() ,且
,且![]() ,
,![]() ,
,![]() ,……,
,……,![]() 组成等差数列,又
组成等差数列,又![]() ,
,![]() 。(1)求数列
。(1)求数列![]() 的通项公式。(2)试比较
的通项公式。(2)试比较![]() 与3的大小,并说明理由。
与3的大小,并说明理由。
解:(1)∵![]() ∴
∴![]() ,即
,即![]()
∴![]() ……① 又∵
……① 又∵![]()
∴![]() ,即
,即![]() 代入①式得
代入①式得![]() ∴
∴![]()
(2)∵![]()
∴![]() 两式相减得
两式相减得
![]() =
=![]()
18、椭圆![]() 上有两点P、Q,O是原点,若OP、OQ斜率之积为
上有两点P、Q,O是原点,若OP、OQ斜率之积为![]() ,
,
(1)求证:![]() 为定值; (2)求PQ的中点M的轨迹方程。
为定值; (2)求PQ的中点M的轨迹方程。
(1)证明:设P、Q的两点坐标分别为P(![]() )、Q(
)、Q(![]() )
)
∵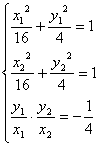
![]()
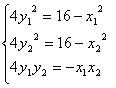 由①
由①![]() ②得
②得![]() +
+![]() … ④
… ④
由③代入④得![]() 由①+②得
由①+②得![]()
∴![]() (定值)
(定值)
(2)设P、Q的中点为M(![]() ),则有
),则有![]()
由①+②+③![]() 2 得
2 得![]()
![]() ∴
∴![]() 即
即![]()
故PQ的中点M的轨迹方程为![]()
19、为了立一块广告牌,要制造一个三角形的支架. 三角形支架形状如图,要求![]() ,BC的长度大于1米,且AC比AB长0.5米. 为了广告牌稳固,要求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
,BC的长度大于1米,且AC比AB长0.5米. 为了广告牌稳固,要求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
解:如图,设BC的长度为x米,AC的长度为y米,则AB的长度
为(y-0.5)米. 在△ABC中,依余弦定理得:
![]() 即
即![]()
化简,得![]() ∵
∵![]() ,∴
,∴![]() 因此
因此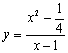
方法一:![]() .
.
当且仅当![]() 时,取“=”号,即
时,取“=”号,即![]() 时,y有最小值
时,y有最小值![]() .
.
 方法二:
方法二: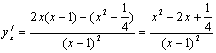 解
解![]() ,得
,得![]()
∵当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
.∴当![]() 时,y有最小值
时,y有最小值![]() .
.
20、已知![]() (
(![]() )
)
(1)求函数![]() 的解析式,当
的解析式,当![]() 是奇函数时,确定常数
是奇函数时,确定常数![]() 的值;
的值;
(2)当![]() 是奇函数时,其单调性如何?试用单调性的定义对称的结论加以证明。
是奇函数时,其单调性如何?试用单调性的定义对称的结论加以证明。
(3)设![]() ,当
,当![]() 是奇函数时,猜想
是奇函数时,猜想![]() 和
和![]() 的大小。(理科用数学归纳法加以证明)
的大小。(理科用数学归纳法加以证明)
解:(1)设![]() 则
则![]()
∴![]() 的解析式为
的解析式为![]() (
(![]() )
)
∵![]() =
=![]()
![]()
∴![]()
∴当![]() 为奇函数时,
为奇函数时,![]() ,且
,且![]() =
=![]()
(2)设![]() ∵
∵![]() =
=![]()
由![]()
![]()
![]() 且
且![]()
![]()
![]() ,即
,即![]() 故
故![]() 是奇函数时,它在R上是增函数。
是奇函数时,它在R上是增函数。
(3)∵![]() ∴设
∴设![]() =
=![]()
当![]() 时,
时,![]() ,故
,故![]()
当![]() 时,
时,![]() 故
故![]()
当![]() 时,
时,![]() 故
故![]()
猜想:当![]() 时,
时,![]() 以下用数学归纳法证明,
以下用数学归纳法证明,
①当![]() 时,猜想成立。
时,猜想成立。
②假设![]() 时,
时,![]()
![]() 成立,则当
成立,则当![]() 时
时
![]()
∵![]() ∴
∴![]() ,即
,即![]()
因此,欲证![]() 只需证
只需证![]() 即可
即可
∵![]() ∴
∴![]()
从而![]() 成立。这就是说当
成立。这就是说当![]() 时
时![]() 成立。
成立。
综合①②可知,当![]() 时,当
时,当![]() 时,
时,![]()
于是当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()