高三数学 第一学期期中试卷
第一学期期中试卷
命题:冯淑平 审核: 金建亚
考生注意:
1.答题前,考生务必用钢笔或圆珠笔清楚填写班级、姓名和学号。
2.本试卷共有22试题,答案直接写在试卷上。
3.本试卷共6页。考试时间120分钟。试卷满分150分。
一. 填空题(本大题满分48分)
1.判断“若![]() ,则
,则![]() .”为______命题.(填“真”,“假”)
.”为______命题.(填“真”,“假”)
2.已知f(x![]() )=lgx,则f(2)=_________.
)=lgx,则f(2)=_________.
3.方程9![]() -3
-3![]() -4=0的解是______________.
-4=0的解是______________.
4.在等差数列![]() 中,a
中,a![]() +a
+a![]() +a
+a![]() +a
+a![]() +a
+a![]() =180,且a
=180,且a![]() =12,则a
=12,则a![]() =__________.
=__________.
5.若数列![]() 为等差数列,且数列前10项的和为10,则
为等差数列,且数列前10项的和为10,则![]() ______.
______.
6.计算:![]()
![]() =_____________.
=_____________.
7.某单位安排7位工作人员在周一到周七值班,每人值班一天,其中甲和乙二人不安排在周一和周二,则不同的安排方法共有________种.(用数值表示)
8.为迎接2010年世博会召开,营造良好的生活环境,上海市政府致力于城市绿化,现有甲,乙,丙,丁4个工程队承包了5个不同的绿化工程,每个工程队至少承包1项工程,那么工程甲承包两项工程的概率是__________.
9.(理)在![]() 的展开式中,系数大于-1的项共有_________项.
的展开式中,系数大于-1的项共有_________项.
(文)设![]() ,变量
,变量![]() 满足
满足![]() ,则
,则![]() 的最小值为_________.
的最小值为_________.
10.已知f(x)是定义在R上的奇函数,当x![]() 0时,f(x)=(
0时,f(x)=(![]() )
)![]() .设f(x)的反函数f
.设f(x)的反函数f![]() (x),则f
(x),则f![]() (0)+f
(0)+f![]() (8)=________.
(8)=________.
11.已知集合A![]() =
=![]() ,则A
,则A![]() 中各元素之和是_______。
中各元素之和是_______。
12.对于实数![]() ,用
,用![]() 表示不超过
表示不超过![]() 的最大整数,则函数f(x)=
的最大整数,则函数f(x)=![]() 称为高斯函数或取整函数.若
称为高斯函数或取整函数.若![]() ,
,![]() 为数列
为数列![]() 的前n项的和,
的前n项的和,![]() =___________.
=___________.
二.选择题(本大题满分16分)
13.设集合S=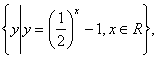 T=
T=![]() ,则S
,则S![]() T=( ).
T=( ).
(A)S
(B)T
(C)R
(D)![]()
14.已知数列![]() 中,a
中,a![]() =(-1)
=(-1)![]() (4n-3),其前n项的和为
(4n-3),其前n项的和为![]()
![]() ,则
,则![]()
![]() -
-![]()
![]() =( )
=( )
(A)-85 (B)85 (C)-65 (D)65
15.“![]() ”是“函数f(x)=
”是“函数f(x)=![]() ,对任意x
,对任意x![]()
![]() ,f(x)>0恒成立”的( )
,f(x)>0恒成立”的( )
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既非充分也非必要条件
16.
已知函数f(x)=![]() ,x
,x![]() .给出下列命题:
.给出下列命题:
① f(x)必是偶函数;②f(0)=f(2)时,f(x)的图像必关于直线x=1对称;
③若![]() ,则f(x)在区间
,则f(x)在区间![]() 上是增函数;④f(x)有最大值
上是增函数;④f(x)有最大值![]() .
.
其中正确的命题个数是______________.
(A)0 (B)1 (C)2 (D)3
三.解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.
17.(本题满分12分)已知函数![]() 的定义域为
的定义域为![]() ,且存在最小值2.
,且存在最小值2.
(1)求a的值。(2)令![]() ,求函数
,求函数![]() 的最小值.
的最小值.
解:
18.(本题满分12分)设数列![]() 是等差数列,
是等差数列,![]() ,前n项和为
,前n项和为![]() ,数列
,数列![]() 是等比数列,
是等比数列,![]() ,其前n项和为
,其前n项和为![]() ,已知
,已知![]()
![]() =16,
=16,![]() .
.
(1)分别求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() 的最大值及此时n的值.
的最大值及此时n的值.
解:
19.(本题满分14分) 已知集合A=![]() ,B=
,B=![]() ,若B
,若B![]() A,
求
A,
求![]() 的取值范围.
的取值范围.
解:
 20.(本题满分14分)已知函数f(x)=
20.(本题满分14分)已知函数f(x)=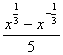 ,
g(x)=
,
g(x)=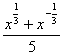 ,
,
(1)判断函数f(x)的奇偶性,求出f(x)的单调区间,并分别说明理由.
(2)分别计算![]() 和
和![]() 的值, 由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式,并加以证明.
的值, 由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式,并加以证明.
解:
 21.(本题满分16分)已知某企业的原有产品每年投入
21.(本题满分16分)已知某企业的原有产品每年投入![]() 万元,可获得的年利润表示为函数
万元,可获得的年利润表示为函数![]() (万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入
(万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入![]() 万元,可获得的年利润表示为函数
万元,可获得的年利润表示为函数![]() (万元).
(万元).
(1)为了解决资金缺口,第一年初向银行贷款1000万元,年利率为5.5![]() (不计复利),第五年底一次性向银行偿还本息共计多少万元?
(不计复利),第五年底一次性向银行偿还本息共计多少万元?
(2)从新产品投入生产的第三年开始,从100万元的生产准备金中,新旧两种产品各应投入多少万元,才能使后三年的年利润最大?
(3)从新旧产品的五年最高总利润中拿出70![]() 来,能否还清对银行的欠款?
来,能否还清对银行的欠款?
解:
22.(本题满分18分)设等比数列![]() 的公比为
的公比为![]() ,前n项和
,前n项和![]()
![]() 0(n=1,2,3,…).
0(n=1,2,3,…).
设![]() ,记
,记![]() 的前n项和为
的前n项和为![]() .
.
(1)求![]() 的取值范围.
(2)用
的取值范围.
(2)用![]() 和
和![]() 表示
表示![]() .
.
(3)试比较![]() 和
和![]() 的大小.
的大小.
解:
高三数学 第一学期期中试卷答案
第一学期期中试卷答案
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]() 6.
6.![]() 7.
7.![]()
8.![]() 9.
9.![]() 10.
10.![]() 11.
11.![]() 12.
12.![]()
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
![]()
17.解:⑴![]() , 由题意得
, 由题意得 ![]() ,
,
![]() 得
得![]() .
.
⑵f(x)=x2-4x+6 ∴![]()
当且仅当![]() 取到最小值
取到最小值![]()
18.解:⑴设{bn}公比为q,由题意得q<1且q≠0,∴![]()
∴![]() 即
即![]() ,∴
,∴![]()
设{an}公差为d,由![]() 得d=2,∴
得d=2,∴![]()
⑵![]()
∴n=3或4时,![]() 有最大值12即Mn最大值为
有最大值12即Mn最大值为![]() .
.
19.解:由![]() 得
得![]() 即(x-3)(x+2)>0 ∴
即(x-3)(x+2)>0 ∴![]()
![]()
当a=0时,![]() 不满足
不满足![]()
当a<0时,![]() 或
或![]() 不满足
不满足![]()
当a>0时,![]() 不满足
不满足![]()
则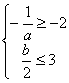 即
即![]() 且
且![]()
综上,a、b的取值范围为![]() 且
且![]()
20.解:⑴函数f(x)的定义域为![]() ,任取
,任取![]()
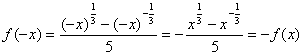 ∴
∴![]() 为奇函数
为奇函数
任取0<x1<x2,
![]()
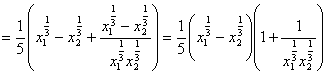
∵![]() ∴
∴![]() ∴
∴![]() 在(0,+∞)上为单调递增
在(0,+∞)上为单调递增
∵f(x)为奇函数 ∴f(x)在![]() 上为单调递增。
上为单调递增。
⑵f(4)-5(f(2)·g(2)=0, f(9)-5f(3)·g(3)=0 ∴f(x2)-5f(x)·g(x)=0
证明: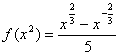 ,
,
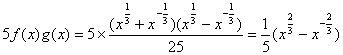
∴![]()
21.解:⑴1000+1000×5.5%×5=1275(万元)
⑵设从第三年起每年旧产品投入x万元,新产品投入100-x万元,则每年的年利润![]()
![]() .
所以投入旧产品27万元,投入新产品73万元时,每年可获最大利润659万元。
.
所以投入旧产品27万元,投入新产品73万元时,每年可获最大利润659万元。
⑶因为P(x)在(0,30)上为增函数,所以前两年利润为![]() (万元)
(万元)
后三年利润![]() (万元)
(万元)
由(20+1977)×70%=1397.9>1275, 故能还清对银行的欠款.
22.解:⑴由题意得![]() .
当
.
当![]() 时,
时, ![]()
当![]() 时,
时, ![]() 即
即![]()
得![]() ①
或
①
或 ![]() ②
②
解①, n可为奇数亦可为偶数, 得![]() .
解②q>1
.
解②q>1
综上, q的取值范围为![]()
⑵![]() 故
故![]() .
.
⑶![]() .
.
∵![]() ,
且
,
且![]() 或
或![]() .
.
∴当![]() 或
或![]() 时,
时, ![]() 即
即![]() .
.
当![]() 且
且![]() 时,
时, ![]() 即
即![]() .
.
当![]() 或
或![]() 时,
时, ![]() 即
即![]() .
.