高三数学调研卷
一、选择题：（本大题每小题5分，共50分．）
（ ）1、已知集合
集合
则
等于 （A）
（B）
（C）
（D）
（ ）2、函数
的反函数是
（A）
（B）
（C）
（D）
（ ）3、设集合
，
，那么“
”是“
”的
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
（ ）4、下列命题：①
或
；②
；③
为有理数，则
、
都是有理数；④对角线相等的四边形是矩形.其中假命题的个数为
A、0 B、1 C、2 D、3
（ ）5、函数
的定义域是
A.
B. 
C. 
D.
（ ）6、函数
的单调递增区间是
A、
B、
C、（0，+∞） D、
（ ）7、已知函数
（1≤x≤3）是单调递增函数，则实数a的取值范围是
A、
B、
C、
D、
（ ）8、已知函数f(x)是定义在R上的奇函数，当x<0时，f(x)＝()x，那么f －1(－9)的值为
A．2 B．－2 C．3 D．－3
（ ）9、对于定义在R上的函数f(x)，若实数x0满足f(x0)=x0，则称x0是函数f(x)的一个不动点，函数f(x)=6x—6x2的不动点是
A、
或0 B、
C、
或0 D、
（ ）10、设二次函数
，若
，则f(m+1)的值是
A、 正数 B、负数 C、非负数 D、与m有关
二、填空题：（本大题每小题5分，共30分．把答案填在题中横线上）
11、设T={(x,y)ax+y-3=0},S={(x,y)x-y-b=0}.若S∩T={(2,1)},则a=_______,b=_______.
12、已知函数
的反函数的图象经过点（4，2），则
的值是_________.
13、设
，
，则
的________条件.
14、已知函数f(x)满足：f(p+q) = f(p) f(q) ，且 f(1)=3, 则
15、设
是定义在R上的奇函数，且在
上单调递增，又
，则
的解集为________
16、已知函数
．给下列命题：①
必是偶函数；②当
时，的图像必关于直线x＝1对称；③若
，则在区间[a，＋∞
上是增函数；④有最大值
．其中正确的序号是________．
三、解答题：（第17、18题12分，第19、20、21题每题14分，第、22题题16分共70分）
17、已知定义在区间[-4，0]上的函数
.（1）求它的反函数;
（2）判断在[-4，0]单调性，并证明;
18、已知二次函数的二次项系数为
，且不等式
的解集为
。（Ⅰ）若方程
有两个相等的根，求的解析式；（Ⅱ）若的最大值为正数，求的取值范围。
19、已知p：方程x2+mx+1=0有两个不等的负实根．q：方程4x2+4（m-2）x+1=0无实根．若p或q为真，p且q为假，求实数m的取值范围。
20、已知函数
满足
，
且
对定义域中的任意x成立，求函数的解析式.
21、设函数
.
（1）在区间
上画出函数
的图像；
（2）设集合
. 试判断集合
和
之间的关系，并给出证明；
（3）当
时，求证：在区间
上，
的图像位于函数图像的上方.
（附加题10分）22、对于在区间[m，n]上有意义的两个函数f (x)与g (x)，如果对任意x∈[m，n]均有 f
(x) – g (x) ≤1，则称f (x)与g (x)在[m，n]上是接近的，否则称f (x)与g (x)在[m，n]上是非接近的，现有两个函数f 1(x)
= loga(x – 3a)与f 2 (x)
= loga
(a > 0，a≠1)，给定区间[a
+ 2，a + 3]．
（1）若f 1(x)与f 2 (x)在给定区间[a + 2，a + 3]上都有意义，求a的取值范围；
（2）讨论f 1(x)与f 2 (x)在给定区间[a + 2，a + 3]上是否是接近的？
高三数学解答
（第Ⅰ卷 选择题部分）
一、选择题：（本大题每小题5分，共60分．在每小题给出的四个选项中,只有一项是符合要求的）
1、已知集合集合则等于（D） （A） （B） （C） （D）
2、函数的反函数是
（A）
（A） （B）
（C） （D）
3、设集合，，那么“”是“”的（ B
）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
4、下列命题：①或；②；③为有理数，则、都是有理数；④对角线相等的四边形是矩形.其中假命题的个数为
A、0 B、1 C、2 D、3
5、函数的定义域是
A. B. C. D.
4．解：由
，故选B.
6、函数的单调递增区间是
A、
B、
C、（0，+∞）
D、
7、已知函数（1≤x≤3）是单调递增函数，则实数a的取值范围是
A、 B、
C、 D、
8、已知函数f(x)是定义在R上的奇函数，当x<0时，f(x)＝()x，那么f －1(－9)的值为
A．2 B．－2 C．3 D．－3
9、对于定义在R上的函数f(x)，若实数x0满足f(x0)=x0，则称x0是函数f(x)的一个不动点，函数f(x)=6x—6x2的不动点是
A、或0 B、
C、或0 D、
10、设二次函数，若，则f(m+1)的值是
B、 正数 B、负数 C、非负数 D、与m有关
高 三 数 学
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
（第Ⅱ卷 非选择部分）
二、填空题：（本大题每小题4分，共16分．把答案填在题中横线上）
11、设T={(x,y)ax+y-3=0},S={(x,y)x-y-b=0}.若S∩T={(2,1)},则a=_______,b=_______.
解析:由S∩T={(2,1)},可知
为方程组
的解，解得
12、已知函数的反函数的图象经过点（4，2），则的值是_________.
13、设，，则的________条件. 充分必要
14、已知函数f(x)满足：f(p+q) = f(p) f(q) ，且 f(1)=3, 则
12
15、设是定义在R上的奇函数，且在上单调递增，又，则的解集为________
16、已知函数．给下列命题：①必是偶函数；②当时，的图像必关于直线x＝1对称；③若，则在区间[a，＋∞上是增函数；④有最大值．
其中正确的序号是________．③
三、解答题：（本大题第17－21题12分，第22题每题14分，共70分）
17、已知定义在区间[-4，0]上的函数.
(1)
求它的反函数; 
(2) 判断在[-4，0]单调性，并证明;
18、已知二次函数的二次项系数为，且不等式的解集为。（Ⅰ）若方程有两个相等的根，求的解析式；
（Ⅱ）若的最大值为正数，求的取值范围。
解：（Ⅰ）
①
由方程
②
因为方程②有两个相等的根，所以
，
即 
由于
代入①得的解析式
（Ⅱ）由
及
由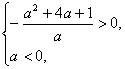
解得 
故当的最大值为正数时，实数a的取值范围是
19、已知p：方程x2+mx+1=0有两个不等的负实根．q：方程4x2+4（m-2）x+1=0无实根．若p或q为真，p且q为假，求实数m的取值范围。
解：由已知p,q中有且仅有一为真，一为假
Δ＞0
p: x1+x2=－m＜0
m＞2
x1·x2=1＞0 (4分)
q∶Δ＜01＜m＜3
若p假q真，则 
若p真q假，则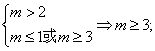
综上所述：所求
的范围是(1,2］∪［3,+∞)。
20、已知函数满足，且 对定义域中的任意x成立，求函数的解析式.
解：由
当
故
（1）
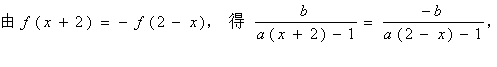
化简，得：
，
.
21、设函数.
（1）在区间上画出函数的图像；
（2）设集合. 试判断集合和之间的关系，并给出证明；
（3）当时，求证：在区间上，的图像位于函数图像的上方.
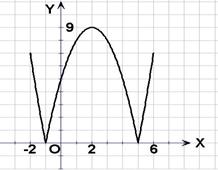34. [解]（1）
……4分
（2）方程
的解分别是
和
，由于在
和
上单调递减，在
和
上单调递增，因此
.
……8分
由于
.
……10分
（3）[解法一] 当
时，
.
，
……12分
. 又
，
①
当
，即
时，取
，
.
，
则
.
……14分
②
当
，即
时，取
， ＝
.
由 ①、②可知，当时，
，.
因此，在区间上，
的图像位于函数图像的上方. ……16分
[解法二] 当时，.
由
得
，
令 
，解得 
或
，
……12分
在区间上，当时，
的图像与函数的图像只交于一点
； 当时，
的图像与函数的图像没有交点.
……14分
如图可知，由于直线过点
，当时，直线是由直线绕点逆时针方向旋转得到. 因此，在区间上，的图像位于函数图像的上方.
（附加题10分）22、对于在区间[m，n]上有意义的两个函数f (x)与g (x)，如果对任意x∈[m，n]均有 f
(x) – g (x) ≤1，则称f (x)与g (x)在[m，n]上是接近的，否则称f (x)与g (x)在[m，n]上是非接近的，现有两个函数f 1(x)
= loga(x – 3a)与f 2 (x)
= loga(a > 0，a≠1)，给定区间[a
+ 2，a + 3]．
（1）若f 1(x)与f 2 (x)在给定区间[a + 2，a + 3]上都有意义，求a的取值范围；
（2）讨论f 1(x)与f 2 (x)在给定区间[a + 2，a + 3]上是否是接近的？
解：（1）要使f 1 (x)与f 2 (x)有意义，则有
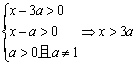
要使f 1 (x)与f 2 (x)在给定区间[a + 2，a + 3]上有意义，
等价于真数的最小值大于0
即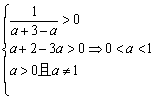
（2）f 1 (x)与f 2 (x)在给定区间[a + 2，a + 3]上是接近的
f 1 (x) – f 2 (x)≤1
≤1
loga[(x – 3a)(x – a)]≤1
a≤(x – 2a)2
– a2≤
对于任意x∈[a + 2，a + 3]恒成立
设h(x) = (x – 2a)2 – a2，x∈[a + 2，a + 3]
且其对称轴x = 2a
< 2在区间[a + 2，a + 3]的左边
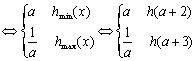
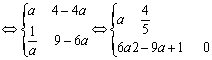
当
时
f 1 (x)与f 2 (x)在给定区间[a + 2，a + 3]上是接近的
当
< a < 1时，f 1 (x)与f 2
(x)在给定区间[a + 2，a + 3]上是非接近的．