高三数学高考模拟题(文科)(三)
考生注意:满分150分,时间120分钟.不准使用计算器.
一、选择题(每小题5分,共50分. 每小题各有四个选择支,仅有一个选择支正确.请把正确选择支号填在答题表内.)
1.已知![]()
A.![]() B.(
B.(![]() ) C.
) C.![]() D.(
D.(![]() )
)
2.下列命题既是全称命题,又是真命题的个数是
(1)对数函数都是单调函数;(2)至少有一个整数,它既能被2整除,又能被5整除;.
(3)对于任意的无理数![]() ,
,![]() 是无理数;(4)存在一整数
是无理数;(4)存在一整数![]() ,使得
,使得![]() .
.
A.1 B.2 C.3 D.4
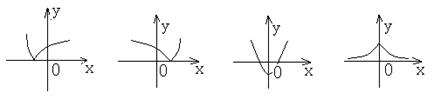 3.函数
3.函数![]() 的大致图象是
的大致图象是
A B C D
4. 已知函数![]() , 则
, 则![]() 与
与![]() 的大小关系是
的大小关系是
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
5. 设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,
则直线![]() 与
与![]() 的位置关系是
的位置关系是
A.平行 B.重合 C.垂直 D.相交但不垂直
6. 已知f (x)的定义在R上的奇函数,它的最小正周期为T,则![]() 的值为
的值为
A.0 B.![]() C.T D.-
C.T D.-![]()
7.已知△ABC中,若=·+·+·,则△ABC是
A.等边三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
 8.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为
8.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为
A.1
B.![]()
C.![]() D.
D.![]() 正视图
侧视图
俯视图
正视图
侧视图
俯视图
9.设![]() 、
、![]() 为曲线
为曲线![]() :
:![]() 的焦点,P是曲线
的焦点,P是曲线![]() :
:![]() 与
与![]() 的一个交点,则
的一个交点,则![]() 的值为
的值为
A.![]() B.
B.![]() C.4
D.3
C.4
D.3
10.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是
A.BC//平面PDF B.DF⊥平面PA E
C.平面PDF⊥平面ABC D.平面PAE⊥平面 ABC
答 题 卷
班级 姓名 得分
一、选择题(每小题5分,共50分.请把正确选择支号填在答题表内.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
 二、填空题(请按要求答题,每小题5分,共20分.
二、填空题(请按要求答题,每小题5分,共20分.
请把答案填在题中的横线上.)
11.复数![]() 的虚部为
的虚部为
12.读下面程序框图,则循环体执行的次数是 ,
程序输出结果是 .
13.球面上有A、B、C三点,AB=AC=2,BC=2![]() ,
,
球心到平面ABC的距离为1,则球的表面积为______.
考生可从下面第14、15两道题中任选一道做答,
若两道题全做答,则只按前一题计算得分.
14.在平面直角坐标系xoy中,圆心在M(1,0)点且过
原点O的圆M的参数方程可写为__________;若以点O
为极点,x轴的正半轴为极轴的直线![]() 的极坐标方程为:
的极坐标方程为:
![]() ,则直线
,则直线![]() 与圆M位置关系为_________.
与圆M位置关系为_________.
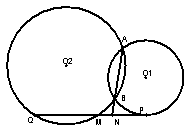 15.如图.⊙
15.如图.⊙![]() 与⊙
与⊙![]() 相交于A、B两点,PQ切⊙
相交于A、B两点,PQ切⊙![]() 于点P,
于点P,
交⊙![]() 于点Q、M,交AB的延长线于点N.若MN=1,MQ=3,
于点Q、M,交AB的延长线于点N.若MN=1,MQ=3,
则NP等于_________
三、解答题(共80分.解答应写出文字说明、证明过程或演算步骤.)
16. 已知 ![]() ,
,![]() ,
,
![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
17.数学测验成绩评定都是正整数,甲、乙两人某次数学测验成绩都是两位正整数,且十位数都是8,求甲、乙两人此次数学成绩的差的绝对值不超过2分的概率.
18.(本小题满分14分)
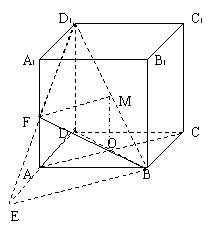
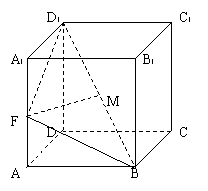 如图,已知棱柱
如图,已知棱柱![]() 的底面是菱形,且
的底面是菱形,且![]() 面
面![]() ,
,![]() ,
,![]() =1,
=1,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,
的中点,
(Ⅰ)求证:![]() 面
面![]() ;
;
(Ⅱ)试判断直线MF与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
19.(本小题满分14分)
已知定点A(0,1)、B(0,![]() )、C(1,0),动点P满足
)、C(1,0),动点P满足![]() .
.
⑴求动点P 点的轨迹D方程;
⑵从轨迹D外一点M点向轨迹D引一条切线,切点为N,且有![]() ,求
,求![]() 的最小值.
的最小值.
20.(本小题满分14分)
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图;由于不慎将部分数据丢失,但知道前4组的频数从左到右依次是等比数列![]() 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列![]() 的前六项.
的前六项.
⑴求等比数列![]() 的通项公式,等差数列
的通项公式,等差数列![]() 的通项公式;
的通项公式;
⑵求最大频率;
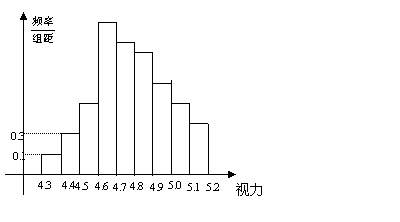 ⑶设
⑶设![]()
![]() ,求数列
,求数列![]() 前2007项和
前2007项和![]() .
.
21.(本小题满分14分)
对于函数![]() ,若同时满足以下条件:
,若同时满足以下条件:
①![]() 在
在![]() 上单调递增或单调递减.
上单调递增或单调递减.
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域也是
上的值域也是![]() ,则称函数
,则称函数![]() 是闭函数.
是闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)当![]() 时判断函数
时判断函数![]() 是不是闭函数?并说明理由;
是不是闭函数?并说明理由;
(3)若函数![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
高三数学高考模拟题(文科)(三)参考答案
一、AAABC ABCDC
二、11.2 12.49; 2450 13.![]() 14.
14.![]()
![]() ;相交
15.2
;相交
15.2
三、16.解:由![]() 得
得![]() ,…………………3分
,…………………3分
![]() 所以
所以![]() , …………………6分
, …………………6分
因为![]() ,所以
,所以![]() , ……………………………………9分
, ……………………………………9分
所以![]()
![]() . …………………………12分
. …………………………12分
17.解:设甲的成绩x、乙的成绩为y
x、y![]()
则(x,y)对应如图所示正方形ABCD及其内部的整数点
共有![]() (5分)
(5分)
其中满足![]() y )对应的点为如图阴影部分(含边界)的整数点,共有
y )对应的点为如图阴影部分(含边界)的整数点,共有
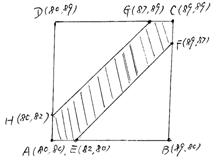
![]() (11分)
(11分)
故所求概率为![]() (12分)
(12分)
解法2:

 故
故 ![]() 80、81、82、83、84时,y共有22种选法 (9分)
80、81、82、83、84时,y共有22种选法 (9分)
同理 ![]() 85、86、87、88、89时,y共有22种选法
(11分)
85、86、87、88、89时,y共有22种选法
(11分)
故所求概率![]() (12分)
(12分)
18.解:(Ⅰ)(方法一)证明:连结![]() 、
、![]() 交于点
交于点![]() ,
,
再连结![]() ……………………1分
……………………1分
![]() 且
且![]() , 又
, 又![]() ,
,
![]() 且
且![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() …………… 3分
…………… 3分
又![]() 面
面![]()
![]() 面
面![]() ……………………………… 5分
……………………………… 5分
(方法二)如图:延长DA至E,使AE=AD,连结BE,证MF‖BE即可.
(Ⅱ)![]() 平面
平面![]() ………… 6分
………… 6分
证明:![]() 底面是菱形,
底面是菱形, ![]()
又![]() 面
面![]() ,
,![]() 面
面![]()
![]() ,
,![]() 平面
平面![]() …………………………………8分
…………………………………8分
![]()
![]() 平面
平面![]() ………………………………10分
………………………………10分
(Ⅲ)过点B作又BH⊥AD于H![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() …………………………………11分
…………………………………11分
在RtΔABHk中,![]() ,AB=1,∴BH=
,AB=1,∴BH=![]() ………………………12分
………………………12分
![]() ……………14分
……………14分
19.解:⑴设动点P![]() ………………………………………………………………1分
………………………………………………………………1分
![]() A(0,1)、B(0,
A(0,1)、B(0,![]() )、C(1,0),动点P满足
)、C(1,0),动点P满足![]()
![]() ,………………………………3分
,………………………………3分
![]()
![]() ……………………………………………5分
……………………………………………5分
因此化简整理得动点P 点的轨迹方程为:![]() ………………7分
………………7分
⑵由⑴知P 点的轨迹方程是一个圆:![]()
由于切线![]() ,
,![]() ……………………………………8分
……………………………………8分
![]()
![]() ,
,![]() ……………………………………9分
……………………………………9分
设![]() ,则
,则![]() ………………………10分
………………………10分
化简得:![]() ,即点M在直线
,即点M在直线![]() 上,……………………12分
上,……………………12分
![]() 的最小值即为
的最小值即为![]() 的最小值
的最小值![]() ………………14分
………………14分
20.解:(1)由题意知:![]()
![]()
因此数列![]() 是一个首项
是一个首项![]() ,公比为3的等比数列,
,公比为3的等比数列,![]() …………3分
…………3分
![]()
又![]()
![]()
![]() ,
,![]() ,
,
因此数列![]() 是一个首项
是一个首项![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,![]() ……6分
……6分
⑵最大频率为:![]() …………………………………………………………8分
…………………………………………………………8分
⑶![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ………………………………………12分
………………………………………12分
又![]() ,
,![]() ,……………………………………………………13分
,……………………………………………………13分
因此数列![]() 是一个从第二项开始的公比为
是一个从第二项开始的公比为![]() 的等比数列,
的等比数列,
![]()
![]() …………………………………………………………14分
…………………………………………………………14分
21.解 (Ⅰ)由![]() =
=![]() 3在[a ,b]上为减函数,
3在[a ,b]上为减函数,
得
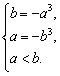 可得a =
–1 , b = 1 ,∴ 所求区间是[–1,1]. ………… 4分
可得a =
–1 , b = 1 ,∴ 所求区间是[–1,1]. ………… 4分
(Ⅱ)取![]() 1 = 1 ,
1 = 1 ,
![]() 2 = 10,可得
2 = 10,可得![]() (
(![]() )不是减函数;取
)不是减函数;取![]() 1 =
1 =![]()
![]() ,可得
,可得![]() (
(![]() )在(0 , +∞)不是增函数,所以
)在(0 , +∞)不是增函数,所以![]() (
(![]() )不是闭函数.
…………7分
)不是闭函数.
…………7分
(Ⅲ)设函数符合条件②的区间为[a
,b],则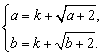
故a , b是方程![]() =
=![]() 的两个实根,命题等价于
的两个实根,命题等价于
![]()
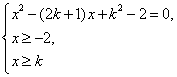 有两个不等实根.
………… 10分
有两个不等实根.
………… 10分
当k![]() 时,
时,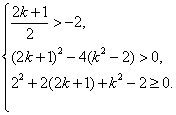 解得:
解得:![]() ,∴
,∴ ![]() ;
;
当![]() 时,
时,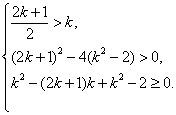 这时
这时![]() 无解.
无解.
所以 k的取值范围是![]() .
………… 14分
.
………… 14分