高三数学理科第一次诊断性测试

高三数学理科第一次诊断性测试

数学（理）

第Ⅰ卷

一、选择题（本大题共12小题，每小题5分，共60分）

1．设为空集，则：　　　　　　　　　　　　　　（　　）

　　A．　　　B． 　　C．　D．

2．有下列四个命题，其中真命题有：

①“若，则互为相反数”的逆命题；

②“全等三角形的面积相等”的否命题；

③“若，则有实根”的逆命题；

④“不等边三角形的三个内角相等”的逆否命题；　　　　　　　　　　　　　　　　　　　　（　　）

　　A．①②　　　　　　 B．②③　　　　　　 C．①③　　 　　　　　D．③④

3．单调增区间为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　 B．

C．　　　　　　　　　　　　　　　　D．

4．若，则a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　B． C．　　　　　 D．

5．数列1，　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　　　　　B．　　　　　　　　　C．　　　　　　　D．

6．已知函数f(x)＝a^x(a>0，且a≠1)的反函数为y＝f^－1(x)，若f^－1(2)+f^－1(5)＝1，则a等于

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．　　　　　　　　　　　B．2　　　　　　　　　　　　C．5　　　　　　　　　　　　D．10

7．已知（m为常数）在[－2，2]上有最大值3，那么此函数在[－2，2]

　 上的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．－5　　　　　　　　　　 B．－11　　　　　　　　　 C．－29　　　　　　　　　 D．－37

8．设函数，对任意实数t都有成立，则函

　 数值中，最小的一个不可能是　　　　　　　　　　　　　　　　　　　　（　　）

A． 　　　　　　 B．　　　　　　　　　C．　　　　　　　　 D．

9、抛物线分圆成的两部分的面积之比为　　　　　　　　　　　　　　　（　　）

A．　　  　 B．　　　 　C．　　  　 D．

10．幂函数的图象过点(2, ), 则它的单调递增区间是　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．(0, ＋∞)　　 　 B．[0, ＋∞]　　 　 C．(－∞, 0)　　 　　D．(－∞, ＋∞)

11．从材料工地运送电线杆到500m以外的公路，英才苑沿公路一侧每隔50m埋栽一根电线杆，已知每次最多只能运3根，要完成运载20根电线杆的任务，最佳方案是使运输车运行

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．11700m　　 　　　B．14700m 　　　　 C．14500m　　　　　D．14000m

12．方程的解所在的区间为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．(0,2)　　　　 　 B．(1,2)　　　　　　 C．(2,3)　　　　 　 D．(3,4)

第Ⅱ卷

二、填空题（本大题共4小题，每小题4分，共16分）

13．一水池有2个进水口，1个出水口，进出水速度如图甲、乙所示. 某天0点到6点，该水池的蓄水量如图丙所示.（至少打开一个水口）

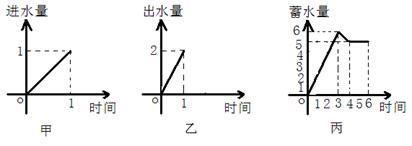给出以下3个论断：①0点到3点只进水不出水；C②3点到4点不进水只出水；③4点到6点不进水不出水.则一定能确定正确的论断序号是_______________.

14．已知直线与抛物线相切，则

15．设p：x－x－20>0,q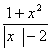：<0,则p是q的　　　　　　  条件.

16．设数列、中，，，，,请按由大到小的次序排列以下各数：、、、…、、、、…、.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

三、解答题

17．（本小题满分12分）

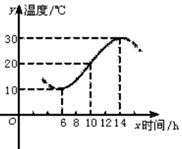
如图，某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.

（1）求这段时间的最大温差.Y

（2）写出这段曲线的函数解析式.

18．（本小题满分12分）

已知

（1）解关于的不等式；

（2）当不等式的解集为（-1，3）时，求实数，的值.

19．（本小题满分12分）

设函数，

　 （I）讨论在内的单调性；

　 （II）求的取值范围，使函数在区间上是增函数.

20．（本小题满分12分）

已知数列{a_n}中，a₁=1，前n项和为S_n，对任意的总成

等差数列.

（1）求a₂、a₃、a₄的值；

（2）求通项公式a_n.

21．（本小题满分12分）

已知函数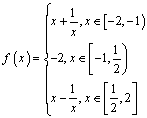

（1）求的值域；

（2）设函数，若对于任意，总存在，使得成立，求实数a的取值范围.

22．（本小题满分14分）

已知，且，数列的前项和为，它满足条件.数列中，·.

（1）求数列的前项和；

（2）若对一切都有，求的取值范围.

参考答案

1—5 BCBCB　 6—10 DDBAC　 11—12 DC

13．1

14．

15．充分不必要

16．、、…、、、、…、、

17．解：(1)由图示，这段时间的最大温差是30－10=20(℃)；

(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象.

∴=14－6,解得ω=,由图示A=(30－10)=10，b=(30+10)=20，这时y=10sin(x+φ)+20,将x=6,y=10代入上式可取φ=π.综上所求的解析式为

y=10sin(x+π)+20,x∈［6,14］.

18．f(1)=－3+a(6-a)+b=-a²+6a+b－3

 ∵ f(1)>0

 ∴ a²－6a+3－b<0

△=24+4b

当b≤－6时，△≤0

∴ f(1)>0的解集为φ；

当b>-6时，

∴ f(1)>0的解集为

　 （2）∵ 不等式-3x²+a(6-a)x+b>0的解集为（-1，3）

∴ f(x)>0与不等式(x+1)(x-3)<0同解

∵ 3x²－a(6－a)x－b<0解集为（－1，3）

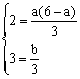∴ 　　　　　解之得

19．（I），

①当

②当0<a<1时，由f′(x)<0,得

由f′(x)>0得

∴当0<a<1时，f(x)在，为增函为函数，

（II）由（I）①知当a≥1时f(x)单调递减，不合；

由②知当f(x)在上单调递增等价于：

，即a的取值范围是

20．解：

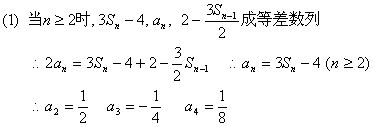
（2）∵当n≥2时，a_n=3S_n-4　 ∴3S_n=3a_n+4

②-①可得：3an+1=an+1-an

　　 ∴　3S_n=a_n+4　　①

　　　　 3S_n+1=a_n+1+4 ②

　　

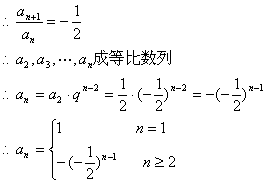
21．解：（1）　　（2）

22．解：（1） 当时，.

当≥2时，=，

此时··=·，

……=……+

设……+，

……，

　　·　　……6分

（2）由可得　当时，由　可得，　对一切都成立，此时的解为.　 当时，由 可得

≥　对一切都成立，

此时的解为.由，可知，对一切都有的的取值范围是或.　　　　　　　　　　　　　　　　　　　…………14分