高三数学2月月考试题

高三数学2月月考试题—

总分１５０分

第Ⅰ卷　(选择题　共60分)

一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)

1.设全集I={1，3，5，7，9}，集合A={1，9，a－5}，_IA={5，7}，则a的值为

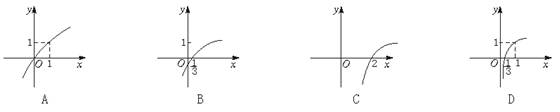
A.2　　　　　　　　B.8　　　　C.－2或8　　　　　 D.2或8　　　　　　　 　　　　　　　　　　　　　 2.已知函数f(x)=3^x－1，则它的反函数y=f^－1(x)的图象是

3.若点P(x,y)在曲线(为参数)上，则使x²+y²取得最大值的点P的　　

坐标是

A.(6，－8)　　　　　　　　　 B.(－6，8)　　　 C.(3，－4)　　 　　 D.(－3，4)　　　 　　　　　　　　　　　　　　　　　　　　　　　

4.(理科)复数等于（　　）

A．　　　　　　　  B．　　　　　　　　 C．　　　　 D．

(文科)若曲线的一条切线与直线垂直，则的方程为（　 ）

A．　 B．　C．　　D．

5.下列命题中，使命题M是命题N成立的充要条件的一组命题是

A.M：a＞b　N:ac²＞bc²

B.M:a＞b,c＞d　N:a－d＞b－c

C.M:a＞b＞0,c＞d＞0　N:ac＞bd  D.M:a－b=a+b　N:ab≤0

6.已知a²=2a·b，b²=2a·b，则a与b的夹角为

A.0°　　　　　　　　　　　　B.30°　　　　C.60° 　　　　 D.180°　　　　　　　  　　　　　　　7.生物学中指出：生态系统中，在输入一个营养级的能量中，大约有10%~20%的能量能够流动到下一个营养级(称为能量传递率)，在H₁→H₂→H₃→H₄→H₅→H₆这条生物链中，若使H₆获得10 kJ的能量，则需要H₁最多提供的能量是

A.10⁴ kJ　　　　　　　　B.10⁵ kJ　　　　  C.10⁶ kJ　　　 　　　　D.10⁷ kJ　　　

8.抛物线y=x²上的两点A、B的横坐标恰是关于x的方程x²+px+q=0(常数p,q∈R)的两个实根，则直线AB的方程是

A.qx+3y+p=0　　　　　　　　B.qx－3y+p=0　　　　C.px+3y+q=0　　　 D.px－3y+q=0　　　　

　　　 9. 在一个口袋中装有5个白球和3个黑球，这些球除颜色外完全相同。从中摸出3个球，至少摸到2个黑球的概率等于　（A）

A　 　　　B　　　　　C　 　　　　D　　　　　　　　　　

10.已知F₁、F₂是椭圆=1(5＜a＜10)的两个焦点，B是短轴的一个端点，则△F₁BF₂的面积的最大值是

A.　　　　　　 B.　　  C.100(3－2)　　　 D.a²　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　

11.△ABC边上的高线为AD，BD=a，CD=b，且a＜b，将△ABC沿AD折成大小为的二面角B—AD—C.若cos=，则三棱锥A—BDC的侧面△ABC是

A.锐角三角形B.钝角三角形C.直角三角形D.形状与a、b的值有关的三角形

12.数列{a_n}中，a₁=1,S_n是其前n项和.当n≥2时，a_n=3S_n，则的值是

A.－　　　　　　　　　　　　 B.－2　　　 C.1　 　　　　  D.－　　　　　　　

二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中横线上)

13.把一个函数的图象按向量a=(3,－2)平移，得到的图象的解析式为y=log₂(x+3)+2，则原来的函数的解析式为___________.

14.在(x²+－4)⁵的展开式中含x⁴项的系数是___________.

15.以椭圆=1的右焦点为圆心，且与双曲线=1的渐近线相切的圆的方程为___________.

16.有下列四个命题：

①若平面的两条斜线段PA、QB在平面内的射影相等，则PA、QB的长度相等　　　 ②已知PO是平面的斜线，AO是PO在平面内的射影，若OQ⊥OP，则必有OQ⊥OA  　③与两条异面直线都平行的平面有且只有一个　④平面内有两条直线a、b都与另一个平面平行，则必有∥　 其中不正确命题的序号为___________.

　　　　　　　　　　　　　　　

高三数学2月月考试题

第Ⅱ卷

答题卡

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

13　　　　　　　  　　14 　　　　　　　 

15　　　　　　　  　　16　　　　　　　 

三、解答题(本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分12分)

讨论函数f(x)=cos(2x－2)+cos²－2cos(x－)cosxcos的值域、周期性、奇偶性及单调性.

18.(本小题满分12分)

在正方体AC₁中，E、F分别为BB₁、CD的中点.

(1)求证：AD⊥D₁F；　　(2)求AE与D₁F所成角的大小；

(3)求证：平面AED⊥平面A₁FD₁.

19.(本小题满分12分)

甲乙两人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判断题4个，甲乙两人依次抽一题.

(1)甲抽到选择题，乙抽到判断题的概率是多少？

(2)甲乙两人中至少有一人抽到选择题的概率是多少？

20.(本小题满分12分).

（理科）设函数f(x)＝(x＋1)ln(x＋1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围．

(文科)已知函数f(x)=x⁵+ax³+bx+1.当x=－1，x=1时，取极值，且极大值比极小值大4.

(1)求a,b的值；　 (2)求f(x)的极大值和极小值

21.(本小题满分12分)

（理科）设双曲线=1的焦点分别为F₁、F₂，离心率为2.

(1)求此双曲线的渐近线L₁、L₂的方程；

(2)若A、B分别为L₁、L₂上的动点，且2AB=5F₁F₂，求线段AB的中点M的轨迹方程并说明轨迹是什么曲线.

(文科)设是一个公差为的等差数列，它的前10项和且成等比数列。　 (I)证明；　　(II)求公差的值和数列的通项公式。

22.(本小题满分14分)

（理科）已知等比数列{a_n}的各项均为正数，且公比不等于1，数列{b_n}对任意自然数n，均有(b_n+1－b_n+2)log₂a₁+(b_n+2－b_n)log₂a₃+(b_n－b_n+1)log₂a₅=0成立，又b₁=t,b₇=13t(t∈R,且t≠0).　　(1)求数列{b_n}的通项公式；

(2)设c_n=，若S_n表示数列{b_n}的前n项和，T_n表示数列{c_n}的前n项和，求.

(文科)设双曲线=1的焦点分别为F₁、F₂，离心率为2.

(1)求此双曲线的渐近线L₁、L₂的方程；

(2)若A、B分别为L₁、L₂上的动点，且2AB=5F₁F₂，求线段AB的中点M的轨迹方程并说明轨迹是什么曲线.

参考答案

一、选择题(每小题5分，共60分)

1.D

2.解析：根据f^－1(x)的定义域及值域观察可得.

答案：D

3.解析：化参数方程为普通方程后得.

答案：A

4.A(理科)  5.D

6.解析：利用cos=.

答案：C

7.C

8答案：C

9A　10.B　11.C

12.解析：由题意得S_n－S_n－1=3S_n,

∴,S₁=a₁=1.

∴S_n=S₁(－)^n－1=(－)^n－1，

=0.

答案：A

二、填空题(每小题4分，共16分)

13.y=log₂(x+6)+4　14.－960

15.(x－5)²+y²=16　16.①②③④

三、解答题(17、18、19、20、21题每题12分，22题14分，共74分)

17.解：利用三角函数公式可化得

f(x)=－cos2x.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

∴f(x)的值域为：［－，］;周期T=；f(x)为偶函数.　　　　　　　　　　　　　　　　9分

当x∈［k,k+］(k∈Z)时 ,f(x)为增函数，

当x∈［k－,k］(k∈Z)时，f(x)为减函数.　　　　　　　　　　　　　　　　　　　 　 12分

18.解：(1)略　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

(2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

(3)通过证明FD₁⊥平面AED得到平面AED⊥平面A₁FD₁.　　　　　　　　　　　　 　 12分

19.解：(1)它是等可能性事件，基本事件总数为CC种，所述事件包含的基本事件数为CC，故所求概率为=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

(2)可直接算也可用求其对立事件的概率来算，结果为.　　　　　　　　　　　　 　 12分

20.(文科)解：(1)f′(x)=5x⁴+3ax²+b,因x=1时有极值，则5+3a+b=0,反代入得：

f′(x)=(x+1)(x－1)(5x²+3a+5).

由题意有5x²+3a+5≠0恒成立，故3a+5＞0,a＞－.

故当x=－1时取极大值，x=1时取得极小值,

且f(－1)－f(1)=4，再由b=－3a－5可解得a=－1,b=－2.　　　　　　　　　　　　　　　　　7分

(2)f(－1)=3为极大值，f(1)=－1为极小值.　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 12分

(理科)解法一：

令g(x)＝(x＋1)ln(x＋1)－ax，

对函数g(x)求导数：g′(x)＝ln(x＋1)＋1－a

令g′(x)＝0，解得x＝e^a－1－1，　　　　　　　  ……5分

(i)当a≤1时，对所有x＞0，g′(x)＞0，所以g(x)在[0，＋∞)上是增函数，

又g(0)＝0，所以对x≥0，都有g(x)≥g(0)，

即当a≤1时，对于所有x≥0，都有　f(x)≥ax．　　……9分

(ii)当a＞1时，对于0＜x＜e^a－1－1，g′(x)＜0，所以g(x)在(0，e^a－1－1)是减函数，

又g(0)＝0，所以对0＜x＜e^a－1－1，都有g(x)＜g(0)，

即当a＞1时，不是对所有的x≥0，都有f(x)≥ax成立．

综上，a的取值范围是（－∞，1]．　　……12分

解法二：令g(x)＝(x＋1)ln(x＋1)－ax，

于是不等式f(x)≥ax成立即为g(x)≥g(0)成立．　　……3分

对函数g(x)求导数：g′(x)＝ln(x＋1)＋1－a

令g′(x)＝0，解得x＝e^a－1－1，　　　　　　　　……6分

当x＞ e^a－1－1时，g′(x)＞0，g(x)为增函数，

当－1＜x＜e^a－1－1，g′(x)＜0，g(x)为减函数，　　……9分

所以要对所有x≥0都有g(x)≥g(0)充要条件为e^a－1－1≤0．

由此得a≤1，即a的取值范围是（－∞，1]．　　……12分

21. .解：(1)渐近线L₁、L₂的方程为x－y=0和x+y=0.　　　　　　　　　　　　　　6分

(2)∵F₁F₂=4，2AB=5F₁F₂，

∴AB=10.

设A在L₁上，B在L₂上，则可以设A(y₁,y₁)、B(－y₂,y₂),　

∴=10.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

设AB的中点M(x,y),

则x=.

∴y₁－y₂=,y₁+y₂=2y,代入①得12y²+=100,

即=1为中点M的轨迹方程，

故轨迹为椭圆.　　　　　　　　　　　　　　　　　　　　

(文科) (I)证明：因成等比数列，故

而　是等差数列，有于是

　　　　 

即　　

化简得　

(II)解：由条件和得到

由(I)，代入上式得　　故

　　　　

因此，数列的通项公式为。。。。。。。。。。。。。。。。。。。。。。。。12分

22.解：(1)设{a_n}的公比为q(0＜q且q≠1).

则a₃=a₁q²,a₅=a₁q⁴,代入已知等式并化简得：

(b_n+2+b_n－2b_n+1)log₂q=0,因为log₂q≠0，

所以b_n+2+b_n=2b_n+1，所以{b_n}为等差数列.

由b₁=t,b₇=13t得b_n=(2n－1)t.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

(2)由于，　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

所以T_n=

而S_n=·n=n²t.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 10分

所以.　　　　　　　　　　　　　　　　　　　　　　　　 　 14分