高三数学5月份考试卷
总分１５０分
一、选择题（本大题共12小题，每小题5分，共60分,每小题只有一个正确答案）
1．函数
的定义域为 （B ）
A．
B．
C．
D．
2．若，p，
成立的一个充分不必要条件是 （ A ）
A．q > p >0 B．p > q >0 C．p < q <0 D．p = q ≠0
3.曲线
的长度是 (A
)
A.
B.
C.
D.
4．在△ABC中，a =
5，b = 8，C = 60°，则
= （ B
）
A．20 B．－20 C．
D．
5．集合P={1，4，9，16…}，若
则
，则运算
可能是 （ D ）
A．加法 B．减法 C．除法 D．乘法
6．在△ABC中，
，若△ABC的最长边为
，则最短边的长为（ D ）
|
C．
D．1
7．
为等差数列，若
，且它的前n项和Sn有最小值，那么当Sn取得最小正值时，n =（ C ）
A．11 B．17 C．19 D．21
8．设对任意实数
，不等式
总成立，则实数a的取值范围是（ C ）
A．
B．
C．
D．
9．已知二面角
的大小为50°，b、c是两条异面直线，则下面的四个条件中，一定
能使b和c所成的角为50°的是 （ C ）
|
B．
C．
D．
10．设圆过双曲线
的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离为 （ B ）
A．4 B．
C．
D．5
11.某校有6间不同的电脑室,每天晚上至少开放2间,欲求不同的安排方案的种数,现有四位同学分别给出下列四个结果:①
;②
;③
;④
.其中正确的结论是
( C )
A.仅有① B.②和④ C.②和③ D.仅有③
12.已知函数
上任一点
处的切线斜率
,则该函数的单调减区间为 (
B )
A.
B.
C.
D.
二、填空题（本大题共4小题，每小题4分，共16分）
13．
的展开式中
的系数是21，则
的系数为
14.已知
,且
都是正数,则
的最小值是________.
15.一项
“过关游戏”规则规定:在第
关要抛掷一颗骰子次,如果这次抛掷所出现的点数之和大于
,则算过关,那么连过前二关的概率是________.
16.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数
的图象恰好通过
个格点,则称函数为
阶格点函数.下列函数:①
;②
;③
;④
,其中是一阶格点函数的有_______.
三、解答题：本大题有6小题，共74分. 解答应写出文字说明，证明过程或演算步骤.
17．（12分）已知向量
，定义函数
．
（1）求
的最小正周期和最大值及相应的x值；（10分）
（2）当
时，求x的值．（2分）
18．（12分）已知函数
．
（1）若在
[1，＋∞
上是增函数，求实数a的取值范围；
（2）若x＝3是的极值点，求在[1，a]上的最小值和最大值．
19. （12分）甲、乙、丙三个口袋内都分别装有6个不相同的球，并且每个口袋内的6个球均有1个红球，2个黑球，3个无色透明的球，现从甲、乙、丙三个口袋中依次随机各摸出1个球.
求：（1）求恰好摸出红球、黑球和无色球各1个的概率；
（2）求摸出的3个球中含有有色球数ξ的概率分布列和数学期望.
20（12分）
|
（I）求侧面PAD与底面ABCD所成的二面角的大小；
（II）求异面直线PD与AE所成角的正切值；
（III）在侧面PAD上寻找一点F，使EF⊥侧面PBC，
试确定点F的位置，并证明你找出的点F满足EF⊥侧面PBC.
21.(12分) 在平面直角坐标系中,O为坐标原点, 给定两点A(1,0)、B(0,2), 点C满足
=α＋β, 其中α, β∈R, 且α2＋β2=1.
(1) 求点C的轨迹方程; 郝 进制作
(2)过点D(2,0)的直线l 和点C的轨迹交于不同的两点M、N, 且M在D、N之间, 记
λ= , 求λ的取值范围
22．（14分）已知
，若数列{an}
成等差数列.
（1）求{an}的通项an;
（2）设
若{bn}的前n项和是Sn，且
答案
一、选择题
BAABD DCCCB CB
二、填空题
13．35 14.
15.
16.①②④
三、解答题
17．解：（１）
--------------------２分
--------------------４分
--------------------６分
．--------------------８分
当
时（９分），取最大值
．--------------------１０分
（２）当
时，
，即
，--------------------１１分
解得
，
．-------------------- 12分
18.解：（1）P=
×
×
×
=.--------------------4
（2）ξ的取值为0，1，2，3，并且
P(ξ=0)=()3=
;P(ξ=1)=
(+)()2=
;
P(ξ=2)=
(+)2()=;P(ξ=3)=
(+)3=.-----------------8
从而ξ的概率分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
并且Eξ=0×+1×+2×+3×=.--------------------12
19．解：（1）
．
∵ x≥1． ∴ 
，-----------------------------------------------------2分
（当x=1时，取最小值）．
∴ a＜3（a＝3时也符合题意）． ∴ a≤3．------------------------------------4分
（2）
，即27-6a+3＝0， ∴ a＝5，
.------------6分
令
得 
，或 
(舍去) --------------------------8分
当
时,
; 当
时,
即当时,有极小值
．又
---------10分
∴ f（x）在
，
上的最小值是，最大值是
. ----------12分
20.解：设底面正方形ABCD的中心为O，边长为
，
由已知得PO⊥平面ABCD，AO=
（I）取AD的中点M，连接MO、PM，
根据已知可得∠PMO为侧面PAD与
底面ABCD所成的二面角的平面角，…………2分
∠PAO为侧棱PA与底面ABCD所成的角，
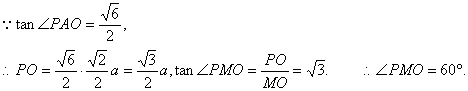
∴侧面PAD与底面ABCD所成的二面角的大小为60°.…………………………4分
（II）连结OE，OE∥PD，
∴∠OEA为异面直线PD与AE所成的角，………………………………………6分
而OE=PD=
∴异面直线PD与AE所成角的正切值为
.………………………………8分
（III）F在线段AD上，且AF=
AD.……………………………………………9分
延长MO交BC于N，取PN的中点G，连结EG、MG，
⊥平面PMN，
∴平面PMN⊥平面PBC，
为正三角形，∴MG⊥PN，
∵平面PMN∩平面PBC=PN，
∴MG⊥平面PBC，∵EG∥MF，∴MF=MA=EG，
∴EF∥MG，∴EF⊥平面PBC.……………………………………………………12分
21. 解(1)设点C(x,y), 则由=α＋β 得 代入α2＋β2=1
得点C的轨迹方程是x2＋ =1 . 郝 进制作
(2)当直线l与x轴重合时, 得N(－1,0), M(1,0), ∴λ= , 当直线l 与x轴不重合时, 设
M(x1,y1),N(x2,y2), 直线l 的方程为x=my＋2(m≠0), 代入4x2＋y2=4中, 得
(4m2＋1)y2＋16my＋12=0, ∴△=162m2－4×12(4m2＋1)>0, 即m2>.
由条件λ= , 得=λ, 且0<λ<1. 郝进 制作
∵ = ＋ +2 = λ＋ ＋2. ∴把* 代入上式, 得
λ＋ ＋2 = = － 由m2> , 得 < <
<λ＋ ＋2< , 即 <λ＋< . 解之, 得< λ< 3. 又∵0<λ<1, ∴< λ<1
综上, 得 ≤ λ<1
22．（14分）解：设2，f(a1), f(a2), f(a3),……，f(an),2n+4的公差为d，则
2n+4=2+(n+2－1)d
d=2,…………………………（2分）
……………………（4分）
（2）
，
