高三数学 [理科]第一轮复习月考试题（3）
总分150分
一．选择题（每小题5分，共60分）
1．全集
=
（A）
（B）
（C）
（D）
2．若函数
对任意x，都有
那么
(A) -2 (B) 2 (C) 
(D) 0
3．函数
的图像关于（ ）对称
（A）直线
（B）原点 （C）y轴 （D）x轴
4．已知
，点P在向量
的延长线上，且
则点P的坐标
（A）（－2，11） （B）
（C）
（D）（－1，8）
5．设
的解集为
（A）
（B）
（C）
（D）
6．已知正数
的最小值是9，则正数a的值是
（A）1 （B）2 （C）4 （D）8
7．向量
的最小值为
（A）
（B）2 （C）
（D）
8．等比数列
中，
（A）33 （B）72 （C）84 （D）189
9．平面直角坐标系中，
为坐标原点，已知两点
，
，若点
满足
，其中
，且
，则点的轨迹方程为
（A）
（B）
（C）
（D）
10．设
是双曲线
的两个焦点，点
在双曲线上，且
，
则
的值等于
（A）2 （B） （C）4
（D）8
11．已知
，则
（A）
（B） （C）1 （D）
12．已知函数
在
上恒为正，则 a的范围
（A）（－2，2） （B）
（C）
（D）
二．填空题（每小题4分，共16分）
13．设
，若
，则P=__▲____
14．已知等比数列的公比
，且
则S100=__▲____
15．若函数
的定义域是[－1, 0]，则
的定义域是__▲____
16．双曲线
的焦点在y轴上，则
的取值范围是 __▲____
三．解答题（第17、18、19、20、21题每题12分，第22题14分，共74分）
17．已知△ABC的面积S满足≤S≤3，且
，设
与
的夹角为
（1）求的取值范围；
（2）求函数
的最小值。
18．已知
成立的x的范围.
19．假设你正在某公司打工，根据表现，老板给你两个加薪的方案：
（Ⅰ）每年年末加1000元； （Ⅱ）每半年结束时加300元。请你选择。
（1）如果在该公司干10年，问两种方案各加薪多少元？
（2）对于你而言，你会选择其中的哪一种？
20．在
中，角
、
、所对的边是
、
、
，且
．
（1）求
值 ；
（2）若
，求面积的最大值．
21．已知二次函数
的图象经过点
，它在
轴上截得的线段长为2，并且对
都有
（1）求的解析式；
（2）若函数
，求
的取值范围。
22．如图，已知椭圆的中心在原点，焦点在x轴上，长轴是短轴的2倍且经过点
．平行于OM的直线l在y轴上的截距为m（
），且交椭圆于A、B两点．
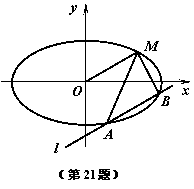（Ⅰ）求椭圆的方程；
（Ⅱ）求m的取值范围；
（Ⅲ）求证直线MA、MB与x轴围成一个等腰三角形．
高三数学 [理科]第一轮复习月考试题（3）
参考答案
一．选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | B | D | A | B | B | D | D | A | A | C |
二．填空题
13．
；14．
；15．
；16．
。
三．解答题
17．（1）∵ ∴
∴
-----2分
又∵
---------------------4分
∴≤
≤3 ∴
≤
≤1--------------------------5分
又∵
∴
≤≤
---------------------------------6分
（2）
-----8分
∵
∴
∴
--------10分
∴当
时 
---------------------------------------------12分
18．解：（1）
……………………2分
1°当m=0时，x>1……………………………………………………………………4分
2°当
①m<0时，x>1或x<
………………………………………………………………6分
②0<m<1时，1<x<………………………………………………………………8分
③m=1时，x∈φ……………………………………………………………………10分
④m>1时，<x<1………………………………………………………………12分
19．设方案一第
年年末加薪
，因为每年末加薪1000元，则
；
设方案二第个半年加薪
，因为每半年加薪300元，则
；………………2分
(1)在该公司干10年(20个半年)，
方案1共加薪
元。…………………………………4分
方案2共加薪 
元. …6分
(2)设在该公司干年，两种方案共加薪分别为：
…………………8分
…………10分
令
，即：
，解得：≥2，当
时等号成立。
∴如果干3年以上(包括3年)应选择第二方案；如果只干2年，随便选；如果只干1年，当然选择第一方案。 …………………12分
20． （1）
，
，
2分
由
，
；6分
（2），且，
，
又
，
，
9分
．
11分
当切仅当
时，面积取最大值，最大值为
． 12分
21．解：（I）解法一、∵
∴二次函数的对称轴为x=2
又函数在x轴上截得的线段长为2，∴可设二次函数为
∵f（x）的图象过点（４，３），∴
∴
∴
…………………………6分
解法二、∵ ∴二次函数的对称轴为x=2
设
图象与x轴交于点 
∵f（x）的图象过点（４，３）∴
∴
∴
，∵
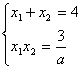，且
∴
，∴ ∴………………………6分
（II）
，
令
， 
当
时，
，
∴
当且仅当
时
任取
∵
，∴
∴
∴
在（0，1）上单调递减，
。
综上，g（x）的取值范围是
……………………………12分
22．解：（Ⅰ）设椭圆方程为
（
），
则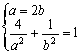
．
∴椭圆方程为
． （…4分）
（Ⅱ）∵直线
且在y轴上的截距为m，∴l：
．
由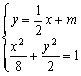
．
∵直线l交椭圆于A、B两点，
∴
（
）． （…8分）
（Ⅲ）设直线MA、MB的斜率分别为
、
，则问题只要证明
．
设
、
，则
、
．
由
，得
，
．
而
…（＊），
又
，
，
∴（＊）分子
．
∴，命题得证． （…14分）