高三数学(不等式)试卷(5)
一、选择(每小题5分共60分)
1. 对于![]() ,给出下列四个不等式
,给出下列四个不等式
①![]() ②
②![]()
③![]() ④
④![]() 其中成立的是
( )
其中成立的是
( )
A.①与③ B.①与④ C.②与③ D.②与④
2.已知![]() ,
,![]() ,当
,当![]() 时,代数式
时,代数式![]() 的值是
的值是
A.正数 B.负数 C.![]() D.介于
D.介于![]() 与
与![]() 之间
之间
3.设函数![]() ,则不等式
,则不等式![]() 的解集为
的解集为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.若实数![]() 、
、![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知三个不等式:![]() (其中a,b,c,d均为实数),用其
(其中a,b,c,d均为实数),用其
中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成的正确命题的个数是
A. 0 B. 1 C. 2 D. 3
6.图像![]() 与函数
与函数![]() 的图像关于
的图像关于
A.直线![]() 对称 B.点
对称 B.点![]() 对称 C.直线
对称 C.直线![]() 对称 D.点
对称 D.点![]() 对称
对称
7.设f(x)和g(x)都是定义域为R的奇函数,
不等式f(x)>0的解集为(m, n), 不等式g(x)>0的解集为(![]() ,
, ![]() ), 其中0< m<
), 其中0< m<![]() , 则不等式f(x)·g(x)>0的解集为
, 则不等式f(x)·g(x)>0的解集为
A (m, ![]() ) B (m,
) B (m, ![]() )∪(-
)∪(-![]() ,-m)
,-m)
C (![]() ,
, ![]() )∪(-n, - m) D
(
)∪(-n, - m) D
(![]() ,
, ![]() )∪(-
)∪(-![]() , -
, -![]() )
( )
)
( )
8、若![]() ,且
,且![]() ,则下列各式中最大的是
(
)
,则下列各式中最大的是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9. 设集合U ={(x,y)|x∈R,y∈R},A={(x,y)|2x-y+m>0},B={(x,y)|x+y-n≤0},那么点P(2,3)∈A ∩(CUB)的充要条件是
A.m>-1且n<5 B.m<-1且n<5 C.m>-1且n>5 D.m<-1且n>5
10. 已知命题P:关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ;命题Q:
;命题Q:![]() 是减函数.若P或Q为真命题,P且Q为假命题,则实数
是减函数.若P或Q为真命题,P且Q为假命题,则实数![]() 的取值范围是
的取值范围是
A.(1,2) B.[ 1,2) C.(-![]() ,1] D.(-
,1] D.(-![]() ,1)
,1)
11. 如果函数![]()
![]() 在区间
在区间![]() 上是增函数,那么实数
上是增函数,那么实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.若函数![]() 在
在![]() 上是奇函数且可导,若
上是奇函数且可导,若![]() 恒成立,且常数
恒成立,且常数![]() ,则下列不等式一定成立的是
,则下列不等式一定成立的是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
二.填空(每小题4分共16分)
12.在![]() 中,
中,![]() 为中线
为中线![]() 上一个动点,若
上一个动点,若![]() ,则
,则![]() 的最小值是
.
的最小值是
.
14.要得到![]() 的图像,且使平移的距离最短,则需将
的图像,且使平移的距离最短,则需将![]() 的图像
的图像
即可得到.
15.已知正数x、y满足x+2y=1,则![]() 的最小值是
.
的最小值是
.
16.已知函数![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的取值范围为
.
的取值范围为
.
三.解答题(6大题,共74分)
17.在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边是
所对的边是![]() 、
、![]() 、
、![]() ,且
,且![]() .(1)求
.(1)求![]() 值 ;(2)若
值 ;(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
18.已知函数![]() 满足
满足![]()
(1)求函数![]() 解析式及定义域; (2)求函数
解析式及定义域; (2)求函数![]() 的反函数
的反函数![]() ; (3)若
; (3)若![]() ,求x的取值范围.
,求x的取值范围.
19.(本小题满分12分)已知函数![]() 的图象与x
的图象与x![]() y轴分别相交于点A
y轴分别相交于点A![]() B,
B,![]() (
(![]()
![]()
![]() 分别是与x
分别是与x![]() y轴正半轴同方向的单位向量), 函数
y轴正半轴同方向的单位向量), 函数![]()
![]()
(1) 求k![]() b的值;
b的值;
(2) 当x满足![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]()
20.(本小题共14分)已知两点![]() ,且动点
,且动点![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求点![]() 的轨迹
的轨迹![]() ;
;
(2)设![]() 、
、![]() 分别是直线
分别是直线![]() 与
与![]() 上的两点,且
上的两点,且![]() 是直线
是直线![]() 的方向向量,直线
的方向向量,直线![]() 与曲线
与曲线![]() 相切,当
相切,当![]() 是以
是以![]() 为底边的等腰三角形时,求
为底边的等腰三角形时,求![]() 的值.
的值.
21.(12分)已知函数f(x)=![]() ,x∈[0,1].
,x∈[0,1].
(1)若f(x)在[0,1]上是增函数,求实数a的取值范围;
(2)求f(x)在[0,1]上的最大值.
22.设Sn是数列![]() 的前n项和,且
的前n项和,且![]() .(1)求数列
.(1)求数列![]() 的通项公式;
(2)设数列
的通项公式;
(2)设数列![]() 使
使![]()
![]() ,求
,求![]() 的通项公式;
(3)设
的通项公式;
(3)设![]() ,且数列
,且数列![]() 的前n项和为Tn,试比较Tn与
的前n项和为Tn,试比较Tn与![]() 的大小.
的大小.
答案
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.D 2.B 3. C 4 D 5.C
6.B 7.B 8C 9.A 10B 11B 12.A
第Ⅱ卷
13.![]() 14.向左平移
14.向左平移![]() 单位 15.
单位 15.
![]() 16.
16.![]()
17.(本小题共12分)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边是
所对的边是![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
(1)求![]() 值 ;
值 ;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
(1)![]()
![]() ,
,![]() ,
,
![]() 2分
2分
由![]() ,
,
![]()
![]() ;
;![]() 6分
6分
(2)![]()
![]() ,且
,且![]() ,
,![]()
![]() ,
,
又![]() ,
,![]() ,
,
![]() 9分
9分
![]() .
.
![]() 11分
11分
当切仅当![]() 时,
时,![]() 面积取最大值,最大值为
面积取最大值,最大值为![]() .
. ![]() 12分
12分
18. (1)设t=x-3,则x=t+3.
∵ ![]() ∴
∴![]() …………1分
…………1分
∵ ![]() ,∴
,∴![]() 由
由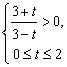 得
得![]() …………2分
…………2分
于是![]() 且定义域为[0,2].
…………1分
且定义域为[0,2].
…………1分
(2)设y=![]() 则
则![]() ,即
,即![]() ,
,
∴![]()
![]() .
…………2分
.
…………2分
∵![]() ∴
∴![]() ,∴
,∴ ![]()
从而![]() .
.
故函数![]() 的反函数为
的反函数为![]()
![]() (
(![]() ).
…………2分
).
…………2分
(3)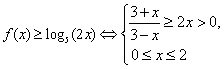
![]()
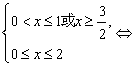
![]()
19.解:(1)
由已知得![]() ,
,![]() …………………………………………2分
…………………………………………2分
则![]() ,于是
,于是![]()
![]() ……………………………………………………4分
……………………………………………………4分
∴![]()
![]() ……………………………………………………………………………6分
……………………………………………………………………………6分
(2) 由![]() ,得
,得![]() ,即
,即![]() , 得
, 得![]()
![]() …………8分
…………8分
![]() =
= ![]()
![]() ………………………………………………10分
………………………………………………10分
由于![]() ,则
,则![]() ,
,
其中等号当且仅当![]() ,即
,即![]() 时成立
时成立![]() ………………………………………12分
………………………………………12分
∴![]() 的最小值是
的最小值是![]()
![]() ……14分
……14分
20.(本小题共14分)已知两点![]() ,且动点
,且动点![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求点![]() 的轨迹
的轨迹![]() ;
;
(2)设![]() 、
、![]() 分别是直线
分别是直线![]() 与
与![]() 上的两点,且
上的两点,且![]() 是直线
是直线![]() 的方向向量,直线
的方向向量,直线![]() 与曲线
与曲线![]() 相切,当
相切,当![]() 是以
是以![]() 为底边的等腰三角形时,求
为底边的等腰三角形时,求![]() 的值.
的值.
(1)设![]() ,由
,由![]() ,得
,得
![]() ,
,![]()
![]() ,
,![]() 3分
3分
于是,![]() ,
,![]() ,
,![]() 成等差数列等价于
成等差数列等价于
![]()
![]()
![]()
![]() 6分
6分
所以点![]() 的轨迹是以原点为圆心,
的轨迹是以原点为圆心,![]() 为半径的圆;
为半径的圆;
![]() 7分
7分
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() 、
、![]() ,
,
![]() 直线
直线![]() 与曲线
与曲线![]() 相切,
相切,![]()
![]() ,即
,即![]()
![]() ①,
①, ![]() 9分
9分
由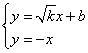
![]()
![]() ,同理
,同理![]() ,
,
![]() 的中点
的中点![]() ,
,
![]() 10分
10分
![]()
![]() 是以
是以![]() 为底边的等腰三角形,
为底边的等腰三角形,
![]() ,即
,即![]()
![]() ②,
②,
![]() 12分
12分
由①②解得![]() .
.
![]() 14分
14分
21解:(1)![]() 在[0,1]恒成立,
在[0,1]恒成立,
![]()
![]()
![]()
![]()
(2)由(1)知,①![]() 时,f(x)在[0,1]是增函数,
时,f(x)在[0,1]是增函数, ![]()
② 当a![]() 0时,易知f(x)在[0,1]是减函数,
0时,易知f(x)在[0,1]是减函数,![]()
③ 当![]() 时,
时, ![]() =0,
=0,![]()
![]() 时,
时,![]() ,
,![]() 时,
时,![]()
![]() 时,f(x)有极大值,也是[0,1]上f(x)的最大值
时,f(x)有极大值,也是[0,1]上f(x)的最大值
![]()
22. ∵![]() ,∴
,∴![]() ,
,
于是an+1=Sn+1-Sn=(2 an+1-2)-(2 an-2),即an+1=2an. …………2分
又a1=S1=2 a1-2, 得a1=2. …………1分
∴![]() 是首项和公比都是2的等比数列,故an=2n.
…………1分
是首项和公比都是2的等比数列,故an=2n.
…………1分
(2) 由a1b1=(2×1-1)×21+1+2=6及a1=2得b1=3. …………1分
当![]() 时,
时,![]()
![]() ,
,
∴![]() .
…………2分
.
…………2分
∵an=2n,∴bn=2n+1(![]() ).
).
∴![]()
(3)![]() .
.
![]() .
.