高三数学(理)第一学期期末考试
说明:本试题分第I卷和第II卷两部分,满分150分,时间120分钟.
第Ⅰ卷(选择题,填空题)
一.选择题(共12小题每小题5分,满分60分)
1. 条件![]() “
“![]() ”, 条件
”, 条件![]() “
“![]() ”,则
”,则![]() 是
是![]() 成立的 ( B )
成立的 ( B )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.非充分非必要条件
2. 已知平面向量![]() ,
,![]() ,且
,且![]() 和
和![]() 共线,则实数
共线,则实数![]() 的值等于( A )
的值等于( A )
A.-2或![]() B.
B.![]() C.2或-
C.2或-![]() D.-
D.-![]()
3. 对于直线![]() ,
,![]() 和平面
和平面![]() ,
,![]() ,
,![]() 的一个充分条件是 (
C )
的一个充分条件是 (
C )
A.![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() B.
B.![]() ⊥
⊥![]() ,
,![]() ∩
∩![]() =
=![]() ,
,![]()
![]()
![]()
C.![]() ∥
∥![]() ,
,![]() ⊥
⊥![]() ,
,![]()
![]()
![]() D.
D.![]() ∥
∥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]()
4.若函数![]() 同时具有以下两个性质:①
同时具有以下两个性质:①![]() 是偶函数,②对任意实数
是偶函数,②对任意实数![]() ,都有
,都有![]() (
(![]() )=
)= ![]() (
(![]() ),则
),则![]() 的解析式可以是
( C )
的解析式可以是
( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 设函数![]() 满足
满足![]() (
(![]() )且
)且![]() , 则
, 则![]() 为 ( B )
为 ( B )
A.95 B.97 C.105 D.192
6. 已知![]() 的顶点都在抛物线上,
的顶点都在抛物线上,![]() 为抛物线的顶点,若直线
为抛物线的顶点,若直线![]() 过抛物线的焦点,则
过抛物线的焦点,则![]() 一定是
( C )
一定是
( C )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.锐角三角形
7. 已知实数![]() 满足:
满足: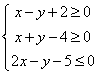 ,则
,则![]() 的最大值为
( D )
的最大值为
( D )
A.18 B.19 C.20 D.21
8. 在函数![]() 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于![]() 的点中,坐标为整数的点的个数是
( D )
的点中,坐标为整数的点的个数是
( D )
A.3 B.2 C.1 D.0
9.若直线![]() 按向量
按向量![]() 平移后与圆
平移后与圆![]() 相切,则
相切,则![]() 的值为( A )
的值为( A )
A.8或-2 B.6或-4 C.4或-6 D.2或-8
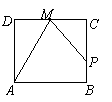
10. 如图,点![]() 在边长为1的正方形
在边长为1的正方形![]() 边上运动,设点
边上运动,设点![]() 是
是![]() 边的中点,点
边的中点,点![]() 沿
沿![]() ®
®![]() ®
®![]() ®
®![]() 运动时,点
运动时,点![]() 经过的路程记为
经过的路程记为![]() ,
,![]() 的面积为
的面积为![]() ,则函数
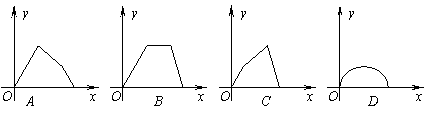
,则函数![]() 的图象只可能是( A ).
的图象只可能是( A ).
11. 已知函数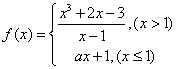 在点
在点![]() 处连续,则
处连续,则![]() = ( D
)
= ( D
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12. 设函数![]()
![]()
![]() ,若
,若![]() 时,
时, ![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
( C )
的取值范围是
( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题(本大题有4个小题,每小题4分,共16分)
13.若焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,则m=_
,则m=_![]() ________.
________.
14.在等比数列![]() 中,已知
中,已知![]() ,
,![]() ,那么
,那么![]()
![]() 。
。
15. 已知![]() 要使
要使![]() 成立,则实数
成立,则实数![]() 的取值范围是 m≥
的取值范围是 m≥![]() 。
。
16. 已知函数![]() .给出下列命题:①
.给出下列命题:①![]() 必是偶函数;②
必是偶函数;②![]() 时,
时,![]() 的图象必关于直线
的图象必关于直线![]() 对称;③若
对称;③若![]() ,则
,则![]() 在区间
在区间![]() 上是增函数;④
上是增函数;④![]() 有最小值
有最小值![]() .
其中正确命题的序号是 ③ .
.
其中正确命题的序号是 ③ .
三.解答题(本大题共6个小题,满分74分,解答时要求写出必要的文字说明或推演步骤).
17.(12分)已知![]() .
.
17. 解法一:由题设条件,应用两角差的正弦公式得
![]() 即
即![]() ①
①
由题设条件,应用二倍角余弦公式得 ![]()
![]() 故
故![]() ②
②
由①式和②式得 ![]() .
.
因此,![]() ,由两角和的正切公式
,由两角和的正切公式
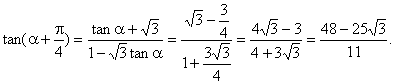
解法二:由题设条件,应用二倍角余弦公式得
![]()
解得![]()
由![]()
由于![]() ,
,
故![]() 在第二象限,于是
在第二象限,于是![]() .
.
从而![]()
以下同解法一.
18.(12分)在正方体![]() 中,如图
中,如图![]() 、
、![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成的角.
所成的角.
18.(12分) 解:建立如图所示的直角坐标系,(1)不妨设正方体的棱长为1,
|
E(1,1,![]() ),F(0,
),F(0,![]() ,0),
,0),
则![]() =(0,
=(0,![]() ,-1),
,-1),![]() =(1,0,0),
=(1,0,0),
![]() =(0,1,
=(0,1,![]() ), 则
), 则![]() =0,
=0,
![]() =0,
=0, ![]() ,
,![]() .
.
![]() 平面ADE.
平面ADE.
(2)![]() (1,1,1),C(0,1,0),故
(1,1,1),C(0,1,0),故![]() =(1,0,1),
=(1,0,1),![]() =(-1,-
=(-1,-![]() ,-
,-![]() ),
),
![]() =-1+0-
=-1+0-![]() =-
=-![]() ,
, ![]() ,
,![]() ,
,
则cos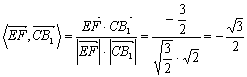 .
. ![]() .
.
19. 已知等差数列![]() 的首项
的首项![]() ,公差
,公差![]() ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列![]() 的第二项、第三项、第四项.
的第二项、第三项、第四项.
(1)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足对任意的
满足对任意的![]() ,均有
,均有![]() 成立,求
成立,求![]()
![]() 的值.
的值.
解:(1)由题意得,![]() ,
,![]() 解得
解得![]() .
.
又![]() ,
,![]() ,
,![]()
在数列![]() 中,公比
中,公比![]() ,
,![]() ,
,![]() .
.
(2) 当![]() 时,
时,![]() ;
;
当![]() 时,由
时,由![]() ,得
,得![]() .
.
![]() 故
故![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
20.某人抛掷一枚硬币,出现正反的概率都是![]() ,构造数列
,构造数列![]() ,使得
,使得![]() ,记
,记![]() .
.
(1) 求![]() 的概率;
的概率;
(2) 求:前两次均出现正面,且![]() 的概率;
的概率;
(3) 记![]() ,求
,求![]() 的数学期望.
的数学期望.
20.解:(1)![]() ,需4次中有3次正面1次反面,设其概率为
,需4次中有3次正面1次反面,设其概率为![]()
则![]()
(2)6次中前两次均出现正面,要使![]() ,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为
,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为![]() 。
。
![]()
(3) ![]()
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]()
21.已知![]() ,
,![]() ,
,![]()
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两端,
两端,![]() ,且有
,且有![]() ,试求
,试求![]() 的取值范围。
的取值范围。
21.解:(1)![]()
![]()
∵![]() ∴
∴![]() =0
=0
∴![]() 得
得![]()
∴P点的轨迹方程为![]()
(2)考虑方程组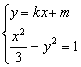 消去y,得(1-3k2)x2-6kmx-3m2-3=0(*)
消去y,得(1-3k2)x2-6kmx-3m2-3=0(*)
显然1-3k2≠0 △=(6km)2-4(-3m2-3)=12(m2+1)-3k2>0
设x1,x2为方程*的两根,则![]()
![]()
![]()
故AB中点M的坐标为(![]() ,
,![]() )
)
∴线段AB的垂直平分线方程为:![]()
将D(0,-1)坐标代入,化简得:4m=3k2-1
故m、k满足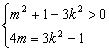 ,消去k2得:m2-4m>0
,消去k2得:m2-4m>0
解得:m<0或m>4
又∵4m=3k2-1>-1 ∴m>-![]() ∴
∴![]() 或
或![]()
22.(本小题满分14分)
已知函数![]() ,
,![]() 的导函数是
的导函数是![]()
![]()
对任意两个不相等的正数![]() ,证明:
,证明:
(Ⅰ)当![]() 时,
时,![]() ;
;
(Ⅱ)当![]() 时,
时,![]()
![]()
22.
证明:(Ⅰ)由![]()
得![]()
![]()
![]()
而![]() ①
①
又![]()
∴![]() ②
②
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() ③
③
由①、②、③得
![]()
即![]()
(Ⅱ)证法一:由![]() ,得
,得![]()
∴![]()
![]()
![]()
下面证明对任意两个不相等的正数![]() ,有
,有![]() 恒成立
恒成立
即证![]() 成立
成立
∵![]()
设![]() ,则
,则![]()
令![]() 得
得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
![]() ∴
∴![]()
∴对任意两个不相等的正数![]() ,恒有
,恒有![]()
证法二:由![]() ,得
,得![]()
∴![]()
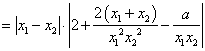
∵![]() 是两个不相等的正数
是两个不相等的正数
∴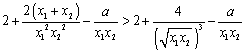
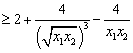
设![]() ,
,![]()
则![]() ,列表:
,列表:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
∴![]() 即
即 ![]()
∴![]()
即对任意两个不相等的正数![]() ,恒有
,恒有![]()