高三数学(理)试卷3YCYYCY
一、选择题:(本大题共12小题,每小题5分,共60分)
1.若集合![]() ,集合
,集合![]() ,则下列各式中正确的是( )
,则下列各式中正确的是( )
A.M∪S=M B.M∪S=S C.M=S D.M∩S=![]()
2.复数![]() 的值是 ( )
的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知P、Q是以C为圆心,半径为![]() 的圆上两点,且
的圆上两点,且![]() 则
则![]() 等于( )
等于( )
A.![]() B.—
B.—![]() C.0 D.
C.0 D.![]()
4.设l1,l2表示直线,![]() 表示平面,若有:①l1⊥l2;②l1⊥
表示平面,若有:①l1⊥l2;②l1⊥![]() ;③l2
;③l2![]()
![]() ,则以其中两个
,则以其中两个
为条件,另一个为结论,可以构成的真命题的个数为 ( )
A.0 B.1 C.2 D.3
5.若函数![]() 的图像关于点
的图像关于点![]() 对称,且在
对称,且在![]() 处函数
处函数
有最小值,则![]() 的一个可能的取值是 ( )
的一个可能的取值是 ( )
A.0 B.3 C.6 D.9
6.已知a>0,b>0,a,b的等差中项为![]() 的最小值为( )
的最小值为( )
A.6 B.5 C.4 D.3
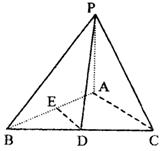
|
∠BAC=90°,英才苑AB≠AC,D、E分别是BC、
AB的中点,AC>AD,PC与DE所成的角为
![]() ,PD与平面ABC所成的角为
,PD与平面ABC所成的角为![]() ,二面角
,二面角
P—BC—A的平面角为![]() ,则
,则![]() ,
,![]() ,
,![]() 的
的
大小关系是( )
A.![]() <
<![]() <
< ![]() B.
B.![]() <
< ![]() <
<![]()
C.![]() <
< ![]() <
< ![]() D.
D.![]() <
<![]() <
< ![]()
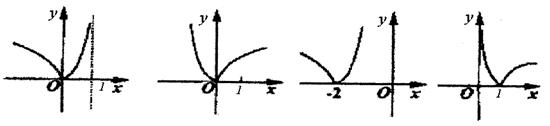
8.已知函数![]() 的图象是 ( )
的图象是 ( )
|
A B C D
9.已知实数x、y满足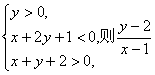 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.过点P(1,1)作曲线y=x3的两条切线l1、l2,设它们的夹角为θ,则tanθ的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知点P是椭圆![]() 上的动点,F1、F2分别为左、右焦点,0为坐标原点,
上的动点,F1、F2分别为左、右焦点,0为坐标原点,
则![]() 的取值范围是 ( )
的取值范围是 ( )
A.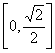 B.
B.![]() C.
C.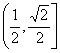 D.
D.![]()
12.数列![]() 存在,则
存在,则![]() =
=
( )
A.![]() B.—
B.—![]() C.±
C.±![]() D.
D.![]()
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中的横线上.
13.若![]() 则a1+a2+a3+…+a11的值为 .
则a1+a2+a3+…+a11的值为 .
14.已知![]() ,英才苑观察下列运算:
,英才苑观察下列运算:
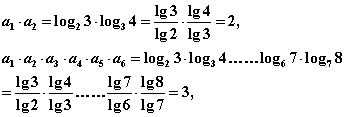
当a1·a2……ak=2008时,k= .
15.将10个相同的小球装入编号为1、2、3的三个盒子中(每次要把10个小球装完),要求每个盒子里小球的个数不小于盒子的编号数,这样的装法共有 种.(用数字作答)
16.给出下列四个命题:
①动点M到两定点A、B的距离之比为常数![]() 则动点M的轨迹是圆;
则动点M的轨迹是圆;
②椭圆![]() ,则b=c;
,则b=c;
③双曲线![]() 的焦点到渐近线的距离是b;
的焦点到渐近线的距离是b;
④已知抛物线y2=2px上两点A(x1, y1),
B(x2, y2),且![]() =0(O为原点),则y1y2=—p2.
=0(O为原点),则y1y2=—p2.
其中的真命题是 .(把你认为是真命题的序号都填上)
答案卷
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:
13. 14. 15. 16.
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
已知A,B是△ABC的两个内角.
(1)若A、B![]() ,求证tanAtanB>1;
,求证tanAtanB>1;
(2)若A,B满足![]() cosA=cos(2B—A),求tan(B—A)tanB的值.
cosA=cos(2B—A),求tan(B—A)tanB的值.
18.(本小题满分12分)
(理)某电讯公司的“电讯咨询热线”电话共有10部,经统计,在每天上午8点至12点这一时间段,同时打入电话的情况如下表:
| 同时打入的电话数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 概率p | 0.13 | 0.35 | 0.27 | 0.14 | 0.08 | 0.02 | 0.01 | 0 | 0 | 0 | 0 |
(Ⅰ)若在上述时间段内,公司只安排2位接线员接听电话(一个接线员一次只能接听一部电话).
①求至少一路电话不能被一次接通的概率;
②在一周的五个工作日中,若有三个工作日在这段时间内至少一路电话不能一次接通,则公司的形象将受到损害,现用“至少一路电话不能一次接通”的概率表示公司形象“损失度”,求在这种情况下公司形象的“损失度”.
(Ⅱ)求一周五个工作日的这一时间内,电话同时打入数ζ的期望.
19.(本小题满分12分)
已知f(x)=x3—3x2—3mx+4(其中m为常数)有极大值为5.
(Ⅰ)求m的值;
(Ⅱ)求曲线y=f(x)过原点的切线方程.
20.(本小题满分12分)
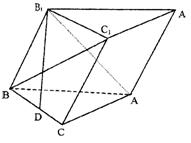
已知斜三棱柱ABC—A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角
为![]() (0°<
(0°<![]() <90°),点B1在底面ABC上的射影D恰好在BC上.
<90°),点B1在底面ABC上的射影D恰好在BC上.
|
(Ⅱ)当![]() 为何值时,AB1⊥BC1,
为何值时,AB1⊥BC1,
且D恰好为BC的中点?
(Ⅲ)当![]() =
=![]() ,AC=BC=AA1时,
,AC=BC=AA1时,
求二面角C1—AB—C的大小.
21.(本小题满分12分)已知双曲线C:![]() 的离心率为
的离心率为![]() ,右焦点
,右焦点
为F,过点(1,0)且斜率为1的直线与双曲线C交于A,B两点,并且![]() .
.
(Ⅰ)求双曲线方程C;
(Ⅱ)过(I)中双曲线C的右焦点F,引直线交双曲线右支于P、Q两点,设P、Q两点在双曲线右准线的射影分别为点C、D,右准线与x轴交于E点,线段EF的中点为M,求证:P、M、D三点共线。
22.(本小题满分为14分)
已知数列{an}满足![]() 的前n项的和,a2=1.
的前n项的和,a2=1.
(Ⅰ)求Sn
(Ⅱ)证明:![]()
数学(理)参考答案
一、选择题:本大题共12小题,每小题5分,共60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | B | B | D | B | A | A | A | B | D | A |
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中的横线上.
13.2 14.22008—2 15.15; 16.①②③
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.(I)因为![]() <A+B<π,
<A+B<π,
所以0<![]() —B<A<
—B<A<![]() ,又y=tanx在(0,
,又y=tanx在(0, ![]() )上为增函数,……3分
)上为增函数,……3分
故tan(![]() —B)<tanA,
—B)<tanA,
所以cotB<tanA,tanAtanB>1………………………………………6分
(Ⅱ)因为![]() cos[B—(B—A)]=cos[B+(B—A)],………………………3分
cos[B—(B—A)]=cos[B+(B—A)],………………………3分
所以(![]() —1)cosBcos(B—A)=—1(1+
—1)cosBcos(B—A)=—1(1+![]() )sinBsin(B—A),
)sinBsin(B—A),
所以,tanBtan(B—A)= ![]() —2……………………………………6分
—2……………………………………6分
18.解:(I)①所求概率为0.14+0.08+0.02+0.01=0.25=![]() .………………3分
.………………3分
②“损失度”为![]() ……………………………… 6分
……………………………… 6分
(Ⅱ)∵在一天的这一时间内,电话同时打入数ξ的期望为
Eξ=0×0.13+1×0.35+2×0.27+3×0.14+4×0.08+5×0.02+6×0.01=1.79,……9分
∴一周五个工作日的这一时间内,电话同时打入数η的期望为
Eη=E(5ξ)=5Eξ=5×1.79=8.95.………………………………………………12分
19.![]()
![]()
二次函数![]() 有极值的条件是
有极值的条件是![]() =0必须有相异两实根.
=0必须有相异两实根.
(1)当△≤0时,即m≤—1时,函数f(x)无极值.
(2)当△>0时,即m>—1时,![]() =0有相异两实根,设两根为α、β(α<β),
=0有相异两实根,设两根为α、β(α<β),
![]() =3(x—α)(x—β),其中
=3(x—α)(x—β),其中![]()
当x变化时,![]() 、f(x)的变化情况如下:
、f(x)的变化情况如下:
| x | (—∞,α) | α | (α,β) | β | (β,+ ∞) |
|
| + | 0 | — | 0 | + |
| f(x) | ↑ | 极大 | ↓ | 极小 | ↑ |

(2)曲线过点![]() ,………………8分
,………………8分
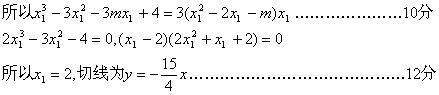
20.(本小题满分12分)解法1(I)∵B1D⊥面ABC,AC![]() 面ABC,∴B1D⊥AC.
面ABC,∴B1D⊥AC.
又∵AC⊥BC且BC∩B1D=D,
则AC⊥面BB1C1C.…………………………………………………………4分
(II)∵AC⊥面BB1C1C,要使AB1⊥BC1,由三垂线定理可知,只须B1C⊥BC1,
∴平面四边形BB1C1C为菱形,此时BC=BB1.
又∵B1D⊥BC,要使D为BC中点,只须B1C=B1B,即△BB1C为正三角形,
∴∠B1BC=60°,∵B1D⊥面ABC,且D落在BC上,
∴∠B1BC为侧棱与底面所成的角,故当![]() =60°时,AB1⊥BC1,且D为BC的中点.……………………………………………………………………8分
=60°时,AB1⊥BC1,且D为BC的中点.……………………………………………………………………8分
(Ⅲ)过C1作C1E⊥BC于E,则C1E⊥面ABC,过E作EF⊥AB于F,连C1F,由三垂线
定理知C1F⊥AB,∴∠C1FE是二面角C1—AB—C的平面角.…………10分
设AC=BC=AA1=a,在Rt△B1BD中,BD=![]()
|
![]()
Rt△CC1F中,EF=B1D=C1E,
∴∠C1FE=45°,
故所求二面角C1—AB—C为45°.…………12分
解法2:(I)同解法1 .……………………………… 4分
(II)要使AB1⊥BC1,D为BC中点,只要使
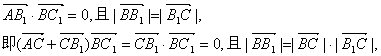
故△BB1C为正三角形,∠B1BC=60°.
又∵B1D⊥面ABC,且D落在BC上,∴∠B1BC即为侧棱与底面所成的角,
故![]() =60°时,AB1⊥BC1,且使D为BC的中点.…………………………8分
=60°时,AB1⊥BC1,且使D为BC的中点.…………………………8分
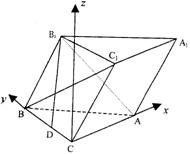
(Ⅲ)以CA所在直线为x轴,CB所在直线为y轴,过C点垂直于平面ABC的直线为z轴,建立空间直角坐标系,则A(a, 0,0),B,(0,a,0),C1![]() ,
,
设平面ABC1的一个法向量![]() =(0,0,1).
=(0,0,1).
设平面ABC1的一个法向量为![]()
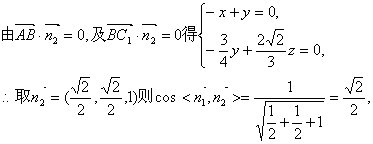
故![]() 所成角为45°,即所求二面角为45°.……………………12分
所成角为45°,即所求二面角为45°.……………………12分
21.解:(1)由已知:b2=2a2,c2=3a2…………………………………………… 1分
直线AB方程为:y=x—1,代入得:x2+2x—1—2a2=0…………………… 2分
x1+x2=—2, x1x2=—2a2—1 y1y2=x1x2—(x1+x2)+1=—2a2+2……………3分
|
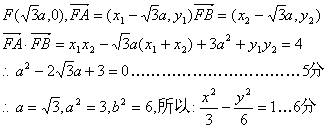
(2)法一:可得焦点F(3,0),M(2,0),
故设直线为x=ty+3,代入![]()
(2t2—1)y2+12ty+12=0,设P(x3,y3), Q(x4, y4)
则![]() ………………8分
………………8分
要证P,M,D三点共线,只须证kPM=kDM即可
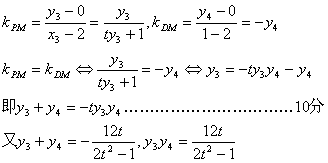
∴y3+y4=—ty3y4 ∴kPM=kDM ∴P,M,D三点共线……………………12分
法二
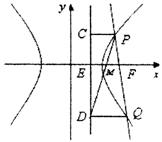
连接PD,设PD与x轴交于点N,
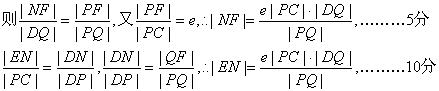
∴NF=EN ∴N是线段EF的中点,所以N,M重合,
∴P,M,D三点共线……………………………………………………12分
22.(1)由题意![]()
两式相减得![]()
所以![]()
所以数列{an}是等差数列.…………………………………………2分
![]()
又a2=1,则公差为1,∴an=n—1,………………………………4分
所以数列{an}的前n项的和为![]() ,…………6分
,…………6分
(2)![]()
①当n=1时:![]()
②当n≥2时:
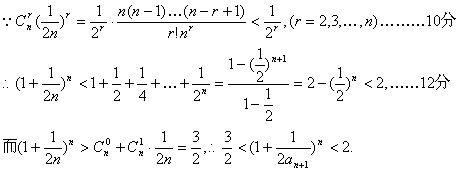
综上所证:![]() …………………………………………14分
…………………………………………14分