高三数学(理)试卷2
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间120分钟。
1.答题前,考生先将自己的姓名、准考证号码填写清楚。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,
字体工整、字迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草
稿纸、试题卷上答题无效。
4.保持卡面清洁,不得折叠、不要弄破、弄皱,不准作用涂改液、刮纸刀。
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.已知三个不等式:![]() ,(其中a,b,c,d均为实数). 用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成正确命题的个数是 ( )
,(其中a,b,c,d均为实数). 用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成正确命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
2.已知等差数列![]() 中,若
中,若![]() ,则这个数列的前9项的和S9等于 ( )
,则这个数列的前9项的和S9等于 ( )
A.66 B.99 C.144 D.297
3.设α是锐角,![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知点O满足![]() ,则O为△ABC所在平面内一点,则点O一定为△ABC的 ( )
,则O为△ABC所在平面内一点,则点O一定为△ABC的 ( )
A.外心 B.内心 C.垂心 D.重心
5.若![]() 是以3为周期的奇函数,且
是以3为周期的奇函数,且![]() ,则a的取值范围是( )
,则a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知x,y满足![]() ,则
,则![]() 的最小值是YC ( )
的最小值是YC ( )
A.0 B.![]() C.
C.![]() D.2
D.2
7.已知![]() ,则使
,则使![]() 在
在![]() 内取到极大值时x的值为( )
内取到极大值时x的值为( )
A.0 B.a C.0 D.-a
8.已知点A(0,-1)和点(4,11),又抛物线![]() 上有一动点P,当抛物线在点P处的切线与直线AB平行时,点P的坐标是
( )
上有一动点P,当抛物线在点P处的切线与直线AB平行时,点P的坐标是
( )
A.(6,9) B.(4,4) C.(2,1) D.(![]() )
)
9.在直二面角![]() 中,直线
中,直线![]() ,直线
,直线![]() 与l斜交,则YCY( )
与l斜交,则YCY( )
A.a不能和b垂直,但可能a//b B.a可能和b垂直,也可能a//b
C.a不能和b垂直,a也不能和b平行 D.a不能和b平行,但可能a⊥b
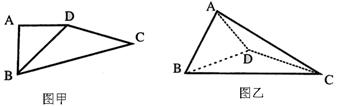
10.如图甲四边形ABCD中,AB=AD,AB⊥AD,![]() ,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A—BCD如图乙,则二面角A—DC—B的正切值( )
,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A—BCD如图乙,则二面角A—DC—B的正切值( )
|
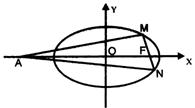
11.已知椭圆E的离心率为e,两个焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个交点,若![]() ,则e的值为
( )
,则e的值为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A. B. C. D.
二、填空题(本在题共4小题,每小题4分,共16分)
13.设![]() ,则
,则
![]() .
.
14.已知数列![]() 中,
中,![]() ,则
,则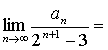 .
.
15.已知点P为圆![]() 上一动点,A(-2,0),B(2,0),点M为直线AP与线段PB的垂直平分线的交点,则点M的轨迹方程为
.
上一动点,A(-2,0),B(2,0),点M为直线AP与线段PB的垂直平分线的交点,则点M的轨迹方程为
.
16.关于两条直线m,n以及两个平面α,β,给出下面命题:
①若m//n,m⊥α则,n⊥α ②若![]() ,则
,则![]()
③若![]() ④若
④若![]()
⑤若![]() ⑥若
⑥若![]()
其中正确命题的序号都有 (请将所有正确命题的序号都添在横线上,答
错、少答或多答均不给分)
英才苑2006年高三名校试题汇编理(30)
一、选择题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
二、填空:13 14 15 16
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)已知函数![]() YCY
YCY
(1)求它的周期和单调递增区间;(2)若![]() ,求它的值域;
,求它的值域;
(3)若关于x的方程![]() 在
在![]() 有且只有一个解,求a的范围.
有且只有一个解,求a的范围.
18.(本小题满分12分)等比数列![]() 同时满足下列条件:①
同时满足下列条件:①![]() ,②
,②![]() ,
,
③三个数![]() 依次成等差数列.
依次成等差数列.
(1)求数列![]() 的通项公式;(2)设Sn是数列
的通项公式;(2)设Sn是数列![]() 的前n项和,证明
的前n项和,证明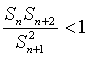 ;
;
(3)记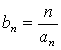 ,求数列
,求数列![]() 的前n项和Tn.
的前n项和Tn.
19.(本小题满分12分)某零售商以每个55元的价格进货了某商品2×104个,根据市场营
销经验,如果按照每个78元卖出,每天将会卖出200个,如果将定价在此价格上增加
![]() 元,其日销量就会少10k个;在此价格上降低
元,其日销量就会少10k个;在此价格上降低![]() 元,其日销量
元,其日销量
就会多40k个. 同时该零售商每天要支出各项费用3240元,请问如何调整价格可使其销
售完该商品后赢得最大利润,最大利润为多少?
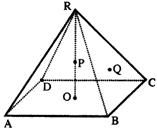
20.(本小题满分12分)已知正四棱锥R—ABCD的底面边长为4,高为6,点O是底面
|
(1)求证:面ROQ⊥面RBC;
(2)求直线PQ与底面ABCD所成的角;
(3)求异面直线PQ与BR所成的角.
21.(本小题满分12分)已知椭圆![]() 的离心率为
的离心率为![]() ,F为椭圆
,F为椭圆
在x轴正半轴上的焦点,M、N两点在椭圆C上,且![]() ,定点A(-4,0).
,定点A(-4,0).
①求证:当![]() 时
时![]() ;
;
②若当![]() 时有
时有![]() ,求椭圆C的方程;
,求椭圆C的方程;
③在②的条件下,当M、N两点在椭圆C运动时,试判断![]() 是否
是否
|
出理由.
22.(本小题满分14分)已知函数![]()
①求证:当![]() 时,恒有
时,恒有![]() ;
;
②求证:当![]() 时,恒有
时,恒有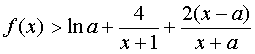 ;
;
③对任意正常数a,求当x在什么范围时,恒有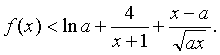
英才苑2006年高三名校试题汇编(理30)
参考答案与评分标准
一、选择题
1.D 2.B 3D 4.C 5.A 6.B 7.C 8.A 9.C 10.C 11.B 12.D
二、填空题:
13.![]() 14.
14.![]() 15.
15.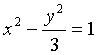 16. ①③⑤⑥
16. ①③⑤⑥
三、解答题:
17.(1)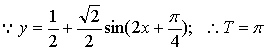 ;……………………2分
;……………………2分
单调递增区间为每一个闭区间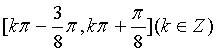 ………………4分
………………4分
(2)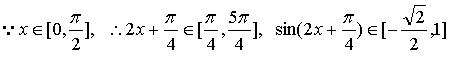 ,
,
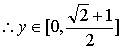 ……………………………………………………8分
……………………………………………………8分
(3)![]() 或
或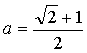 ………………………………12分
………………………………12分
18.(1)由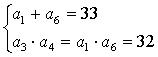 ,得
,得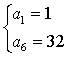 或
或 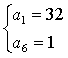 ,
,
![]() 或
或 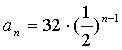 ,又
,又![]() 依次成等差数列,
依次成等差数列,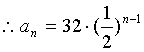
舍,所以数列![]() 的通项公式为
的通项公式为![]() .……………………………………4分
.……………………………………4分
(2)由![]() ,得
,得![]() ,
,
所以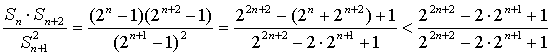 =1
=1
所以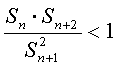 ………………………………………………8分
………………………………………………8分
(3)因为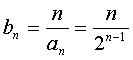 ,所以
,所以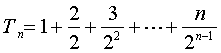 , ①
, ①
![]() ,
②
,
②
①—②得:![]() ,所以
,所以![]()
…………………………12分
19.解:当定价比78元增加k元时,利润为
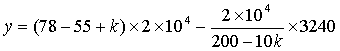 …………………………2分
…………………………2分
![]() (当k=2时取等号)……5分
(当k=2时取等号)……5分
当定价比78元减少k元时,利润为
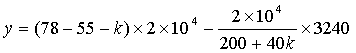 ……………………7分
……………………7分
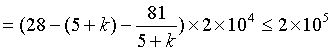 (当k=4时取等号)………10分
(当k=4时取等号)………10分
比较两种情况可得当售价定为74元时,可取得最大利润为![]() 元………12分
元………12分
20.(1)∵正四棱锥R—ABCD中Q是△RBC的重心,∴RQ⊥BC
又∵RO⊥底面ABCD,∴RO⊥BC,∵RO∩RQ=R,∴BC⊥平面ROQ
∴平面ROQ⊥平面RBC ………………………………………………4分
(2)延长RQ交BC于点M,由PQ与OM不平行且共面,所以它们必相交,
设RQ∩OM=N,则∠PNO为直线PQ与底面ABCD所成的角,
可求得![]() ,即直线PQ与底面ABCD所成的角为
,即直线PQ与底面ABCD所成的角为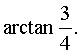 ……8分
……8分
(3)在BC上取一点K,使![]() 则
则![]()
计算可得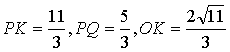 ,
,
由此可求得PQ与BR所成的角为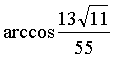 ………………12分
………………12分
21.(1)设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
由M,N两点在椭圆上,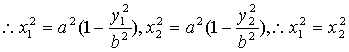
若![]() ,则
,则![]() 舍,
舍,![]()
![]() ……………………2分
……………………2分
(2)当![]() 时,不妨设
时,不妨设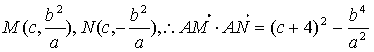
又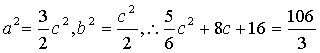 ,
,
![]() ,椭圆C的方程为
,椭圆C的方程为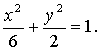 ………………………………5分
………………………………5分
(3)![]() ,
,
设直线MN的方程为![]()
联立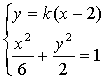 ,得
,得![]() ,
,
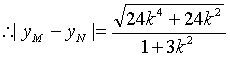 ………………………………7分
………………………………7分
记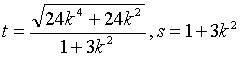 ,
,
则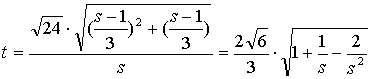
![]() ,当
,当![]() ,即
,即![]() 时取等号 ……………………9分
时取等号 ……………………9分
并且当k=0时![]() ,
,
当k不存在时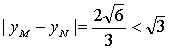
综上![]() 有最大值,最大值为
有最大值,最大值为![]()
此时MN的直线方程为![]() ,或
,或![]() ,………………12分
,………………12分
22.(1)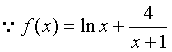 ,
,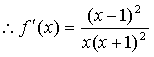 ,
,
当![]() 时,
时,![]() 上为增函数. ………………2分
上为增函数. ………………2分
![]() 在
在![]() 处连续,且
处连续,且![]() 即
即![]() ……5分
……5分
(2)当![]() 时,
时,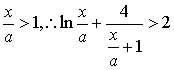 ①,
①,
要证![]() ,即证
,即证![]() ,
,
由①式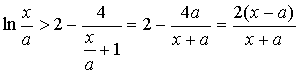 ,所以原式成立. ………9分
,所以原式成立. ………9分
(注:本问也可类似第3问的思路构造函数求导来证明)
(3)要使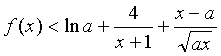 恒成立,需
恒成立,需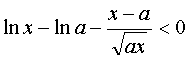 恒成立
恒成立
记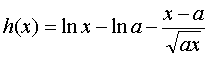 ,则
,则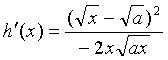 ………11分
………11分
当![]() 时
时![]() ,当
,当![]() 时也有
时也有![]() ,
,
且![]() 在
在![]() 处连续,所以
处连续,所以![]() 在
在![]() 上为减函数
上为减函数
由![]() ,所以只有当
,所以只有当![]() 时恒有
时恒有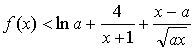 …14分
…14分