高三数学(理)试卷
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k 次的概率Pn(k)=![]()
球的表面积公式S=4πR2(其中R表示球的半径)
球的体积公式:![]() (其中R表示球的半径
(其中R表示球的半径
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的.
|
A. B.{0} C.{1} D.{0,1}
2.已知不等式![]() 的解集为
的解集为![]() ,则实数a ( )
,则实数a ( )
A.-3 B.-1 C.1 D.3
3.长方体ABCD—A1B1C1D1中,AB=BC=1,AA1=3,则异面直线AC与BC1所成角的余弦
值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.复数![]() 的虚部为 ( )
的虚部为 ( )
A.-3 B.3 C.-3i D.3i
5.过原点作曲线C: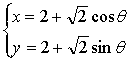 (
(![]() 为参数)的两条切线,则这两条切线的夹角为
为参数)的两条切线,则这两条切线的夹角为
A.30° B.45° C.60° D.90°
6.已知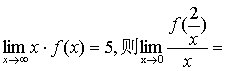 ( )
( )
A.0 B.![]() C.5 D.10
C.5 D.10
7.双曲线![]() 的左右焦点分别是F1、F2,线段F1F2被抛物线
的左右焦点分别是F1、F2,线段F1F2被抛物线![]()
的焦点分成5:3的两段,那么双曲线的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知O为△ABC所在平面上的一点,满足![]() ,且
,且![]()
=![]() ,则三角形为 ( )
,则三角形为 ( )
A.正三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形
9.连续掷一枚骰子3次,三次点数之和为10的不同抛掷结果有 ( )
A.27种 B.30种 C.33种 D.36种
10.将数列![]() 按“第n组有n个数”的规则分组如下:(1),(3,9),(27, 81,243),…,则第100组中各数之和为 ( )A.
按“第n组有n个数”的规则分组如下:(1),(3,9),(27, 81,243),…,则第100组中各数之和为 ( )A.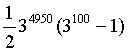 B.
B.![]()
C.![]() D.
D.![]()
11.已知地球半径为R,A地在北纬60°东经20°,B地在北纬30°西经70°,英才苑则A,B的球面距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.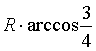
12.已知![]() 满足
满足![]() ,则
,则![]() 在区间[0,
在区间[0,![]() ]上的最大值和最小值之和为 ( )
]上的最大值和最小值之和为 ( )
A.![]() B.
B.![]() C.
C.![]() D.-
D.-![]()
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把正确答案填题卡中的横线上.
13.已知![]() ,则
,则![]() =
.
=
.
14.已知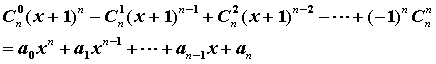 ,
,
则![]() =
.
=
.
15.有一边长分别为8与5的长方形,在四个角各剪去相同的小正方形,把四边折起做成一个无盖小盒,要使纸盒的容积最大,则剪去的小正方形的边长应为 .
16.函数![]() ,对任意
,对任意![]() ,有下列命题中正确的命题题号为
,有下列命题中正确的命题题号为
①![]() ②
②![]()
③![]() ④
④![]()
英才苑2006年高三名校试题汇编(59)(理)2006.5
二、填空:13 14 15 16
三、解答题:本大题共6小题,共74分. 解答应写出文字说明、证明过程或演算步骤,解答过程书写在答题纸的对应位置.
17.(本小题满分12分)
|
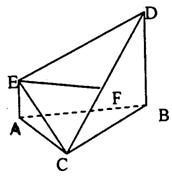
(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成的二面角的正弦值.
18.(本小题满分12分)
已知O为坐标原点,英才苑![]()
![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若![]() 的定义域为
的定义域为![]() ,值域为[2,5],求a,b的值
,值域为[2,5],求a,b的值
19.(本小题满分12分)
数列![]() 满足
满足![]() ,且
,且![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)记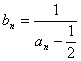 ,求数列
,求数列![]() 的前n项的和.
的前n项的和.
20.(本小题满分12分)
有甲、乙两个箱子,甲箱中有6张卡片,其中2张写有数字0,2张写有数字1,2张写有数字2,乙箱中也有6张卡片,其中3张写有数字0,2张写有数字1,1张写有数字2. 现从甲箱中取1张卡片,从乙箱中取2张卡片.
(1)求至少有两张卡片写有数字0的概率;
(2)设取出3张卡片数字之积为ξ,求ξ的分布列及数学期望.(用分数作答)
|
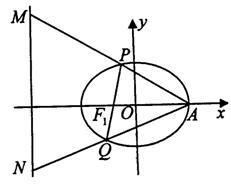
已知椭圆![]() ,F1为其左
,F1为其左
焦点,A为右顶点,l为左准线,过F1的直线![]()
与椭圆交于异于A的P、Q两点.
(1)求![]() 的取值范围;
的取值范围;
(2)若AP∩l=M,AQ∩l=N,求证:M,
N两点的纵坐标之积为定值.
22.(本小题满分14分)
设函数![]() ,其图象在
,其图象在![]() 处的切线的斜率分别为0,-a.
处的切线的斜率分别为0,-a.
(1)求证:![]() ;
;
(2)若函数![]() 的递增区间[s,t],求s-t的取值范围.
的递增区间[s,t],求s-t的取值范围.
(3)若当![]() 时,(
时,(![]() 是与a,b,c无关的常数),恒有
是与a,b,c无关的常数),恒有![]() ,试求
,试求![]() 的
的
最小值.
参考答案59
1—5:DDCBC 6—10:BCAAA 11—12:DB
|
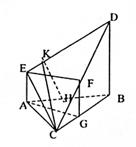
17.解(1)取BC中点G,连结FG,AG
∵AE⊥面ABC,BD∥AE,∴BD⊥面ABC,
又AG![]() 面ABC,∴BD⊥AG,
面ABC,∴BD⊥AG,
又AC=AB,G是BC中点,∴BC⊥AG,
∴AG⊥面BCD,………………3分
∵F是CD的中点且BD=2,∴FG∥BD
且FG=![]() BD=1,
BD=1,
∴FG∥AE 又AE=1,∴AE=FG,故四边形AEFG是平行四边形,从而EF∥AG
∴EF⊥面BCD ………………6分
(2)取AB的中点H,则H为C在面ABDE上的射影,过C作CK⊥DE于E,连接
KH,由三垂线定理的逆定理得KH⊥DE,∴∠HKC为二面C—DE—B的平面角,9分
易知EC=![]() ,DE=
,DE=![]() ,CD=2
,CD=2![]() ,EF=
,EF=![]() ,
,
由![]() ,可得
,可得![]() ,
,
Rt△CHK中,sin∠HKC=![]()
∴面CDE与面ABDE所成的二面角的正弦值为![]() .…………………………12分
.…………………………12分
18.解:(1)![]()
![]() ……………2分
……………2分
![]() 时,由
时,由![]() 得
得
![]() 的单调递增区间为
的单调递增区间为![]() ……………………4分
……………………4分
![]() 时,由
时,由![]() 得
得
![]() 的单调递增区间为
的单调递增区间为![]() ………………6分
………………6分
(2)![]()
![]() ……………………7分
……………………7分
![]() 时,
时,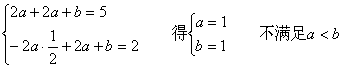 ,舍…………9分
,舍…………9分
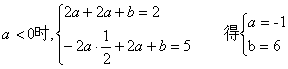 ………………11分
………………11分
综上,a=-1,b=6…………………………12分
19.(1)由![]() 得
得![]() ……………………2分
……………………2分
![]() …………………………4分
…………………………4分
所以![]() 是首项为
是首项为![]() ,公比q=2的等比数列,故
,公比q=2的等比数列,故![]() ,
,
即![]() .……………………6分
.……………………6分
(2)由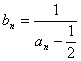 得
得![]() ,……………………8分
,……………………8分
![]()
故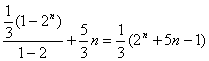 …………………………12分
…………………………12分
20.解(1)![]() ,………………4分,
,………………4分,
(2)随机变量ξ的分布列为:
| ξ | 0 | 1 | 2 | 4 |
| P |
|
|
|
|
………………………………………………10分
期望为![]() …………………………………………12分
…………………………………………12分
21.解:(1)当直线PQ的斜率不存在时,PQ方程为x=-1,代入椭圆![]()
得![]() ……1分
……1分
当直线PQ的斜率存在时,设PQ方程为![]()
代入椭圆![]() 得
得![]() ………………2分
………………2分
设![]() 得
得![]()
![]() …………3分
…………3分
![]()
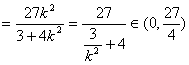 ………………5分
………………5分
综上,![]() 的取值范围是(
的取值范围是(![]() ………………6分
………………6分
(2)AP的方程为![]() 与l的方程:
与l的方程:![]() 联立得
联立得![]() ……8分
……8分
同理,得![]() ……………………9分
……………………9分
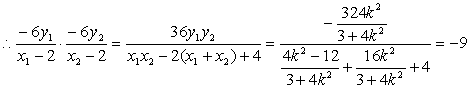 ………11分
………11分
∴M,N两点的纵坐标之积为定值-9………………12分
22.解:(1)![]()
由题意,得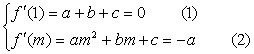 ……………………2分
……………………2分
又![]() 得
得![]()
由(1)得![]() ,代入
,代入![]() 得
得![]()
由![]() 得
得![]() ………………2分
………………2分
将![]() 代入(2)得,
代入(2)得,![]() (3)
(3)
由(3)有实根,得![]() 即
即![]()
解得![]() 或
或![]() …………4分
综上,
…………4分
综上,![]() ………………5分
………………5分
(2)由![]() 的判别式
的判别式![]() 得
得
![]() 有两个不等实根,设为
有两个不等实根,设为![]()
又![]() 知
知![]() 是方程的根,
是方程的根,![]()
当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时
时![]() …………7分
…………7分
∴函数![]() 的递增区间为
的递增区间为![]() ………9分
………9分
(3)由![]() ,即
,即![]() 即
即![]()
![]()
设![]() 对
对![]() 恒成立 ………………11分
恒成立 ………………11分
![]() 即
即 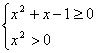 得
得![]() 或
或![]() ………………13分
………………13分
![]() 因此k的最小值为
因此k的最小值为![]() .…………………………14分
.…………………………14分