高三数学（文）试卷
命题人：郑锡华 总分150分
一、选择题（10×5分＝50分，在每小题给出的四个选项中，只有一项是符合要求的）
1. 已知集合
，则集合
=
A．{
}； B．{
}； C．{
}； D． {
}
2. 对于平面
和共面的直线
、
下列命题中真命题是
A．若
则
B．若
则
C．若
则 D．若、
与所成的角相等，则
3. 不等式
成立的充分不必要条件是
A．
或
； B．
或
； C．
； D．
4. 如图，一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的体积为
A．1 B、
C、
D、
5．函数
的图象经过点
,则该函数的一条对称轴方程为
A．
B．
C．
D．
6．若平面四边形
满足
,
,则该四边形一定是
A．直角梯形 B．矩形 C．菱形 D．正方形
7、甲、乙、丙、丁四位同学各自对
、
两变量的线性相关性作试验，并用回归分析方法分别求得相关系数
与残差平方和如下表：
| 甲 | 乙 | 丙 | 丁 | |
|
| 0.82 | 0.78 | 0.69 | 0.85 |
|
| 115 | 106 | 124 | 103 |
则哪位同学的试验结果体现、两变量更强的线性相关性
A、 甲 B、乙 C、 丙 D、 丁
8、若抛物线
的焦点与椭圆
的右焦点重合，则
的值为
A．
B．
C．
D．
9、命题
，命题
的解集是
，
给出下列结论，其中正确的选项是
①命题“
”是真命题； ②命题“
”是假命题；
③命题“
”是真命题； ④命题“
”是假命题
A、②③ B、①②④ C、①③④ D、①②③④
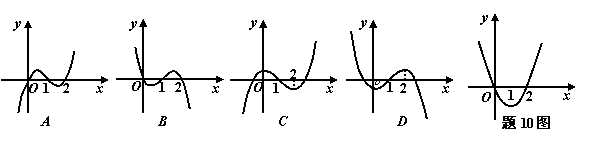10、函数
的导函数
的图象如右图所示，则
的图象最有可能的是
二、填空题（4×5分＝20分。把答案填在题中横线上）
11、函数
的值域是
。
12、A、B是x轴上两点，点P的横坐标为1，且
，若直线PA的方程为
，
则直线PB的方程为 。
|
13. 右图给出的是计算
的值的一个
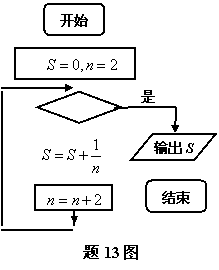
程序框图,其中判断框内应填入的条件是__________。
14、某公司一年购买某种货物400吨，每次都购买
吨，
运费为4万元/次，一年的总存储费用为
万元，
要使一年的总运费与总存储费用之和最小，则
吨．
三、解答题（6小题，共80分，解答应写出文字说明，证明过程或演算步骤）
15、（满分12分）已知函数
。
(Ⅰ)求的定义域；(Ⅱ)设α是第四象限的角，且tan
=
，求
的值.
16、（满分14分）已知向量
，
在＝1处有最大值，（1）求t的值；（2）求使
的的取值范围。
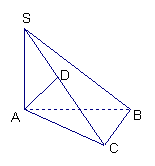17、（满分12分）已知
中∠ACB＝90°，SA⊥面ABC，AD⊥SC于D，
且AB＝5，BC＝4，SA＝3 。（1）求证： AD⊥面SBC；（2）求三棱锥A—SBC的体积。
提示：不在该区域内答题
18、（满分14分）在两个口袋里分别装有编号为1，2，3，4，5，6的小球，从两个口袋里先后各摸出一个球，用两个小球上的编号组成一个两位数字的号码。
问：（1）用列表法写出所有不同的结果？（2）数字大于20的号码有多少个？
（3）数字大于20的号码的概率是多少？
19、（满分14分）设{
}为等差数列，{ 
}为各项为正的等比数列，且
，
，
，分别求出数列{}和{}的前10项和
及
．
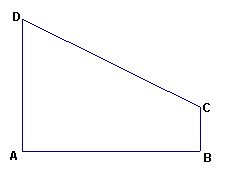
20、(满分14分)如图，在直角梯形中，
，
，
，
，
，椭圆以
、
为焦点且经过点
．（Ⅰ）建立适当的直角坐标系，求椭圆的方程；（Ⅱ）以该椭圆的长轴为直径作圆，判断点C与该圆的位置关系。
答案：
1-10 CCDD CCDD DC
11、R ；12、x+y-3=0 ；13、i≥11，或i＞10； 14、20
15、解：(Ⅰ)由
得
（k∈Z),
故的定义域为｛x,k∈Z｝.
(Ⅱ)因为tanα=,且α是第四象限的角, 所以sinα=
,cosα=
,
故=
=
= 
=
.
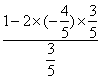16、（1）t=1；（2）略
17、证明：（1）
（1分）
又
面
（2分）
又AC∩SA=A, 
面
（5分）
∵ AD
平面SAC，
（6分）
又
面
（8分）
（2）6
18、（1）36；（2）20；（3）5/6
19、
；
20、解：（Ⅰ）以
所在直线为轴，的垂直平分线为
轴建立直角坐标系……1分
则
，
，
，
…3分
设椭圆方程为
……4分
则
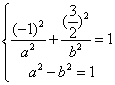解得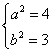
………………8分
∴所求椭圆方程为
………………9分
（2）点C在圆内