高三数学（文科）（10月）阶段考试题
制卷人 周祖勇
一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)
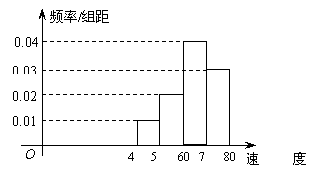1、如图是150辆汽车通过某路段时速度的频率分布直方图，则速度在
的汽车大约有（ ）
A、100辆 B、80辆 C、60辆 D、45辆
2、在数列
中，如果存在非零常数
，使得
对于任意的非零自然数
均成立，那么就称数列
为周期数列，其中叫数列
的周期。已知数列
满足
，如果
，当数列
的周期最小时，该数列前2005项的和是
( )
A．668 B．669 C．1336 D．1337
3、下列所给的4个图象为我离开家的距离y与所用时间t 的函数关系
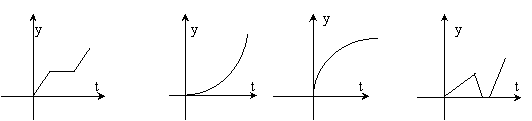
① ② ③ ④
给出下列3个事件：
（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再去上学；
（2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．
其中事件（1）（2）（3）与所给图象吻合最好是 ( )
A. ④①② B.③①② C.②①④ D.③②①
4、已知函数
在区间(
，1)上有最小值，则函数
在区间(1，
上一定（）
A．有最小值 B．有最大值 C．是减函数 D．是增函数
5、 已知命题甲：
，命题乙：点
是可导函数
的极值点，则甲是乙的（）
A、充分而不必要条件 B、必要而不充分条件
C、充要条件 D、既不充分而不必要条件
6、函数f（x）的定义域是[
，2]，则y=f(log2x)的定义域是 ( )
A、[-1,1]
B、[
] C、[
, 4] D、 [1, 4]
7、已知
，则a＋b的值所在的区间是 （ ）
A、（0，1） B、（1，2） C、（2，3） D、（3，4）
8.、函数
的图象是曲线C，则曲线C与直线
（）
A、一定有一个交点 B、至少有一个交点
C、最多有一个交点 D、有无数个交点。
9、已知函数f(x)=x2,集合A={xf(x－1) =ax,x∈R}，且A∪{xx是正实数}={xx是正实数}，则实数a的取值范围是（ ）
A.（－4,+∞） B.（－∞，－1
C.（0,+∞） D.（－∞,－4∪[0,+∞
10、当0≤x≤1时，函数y=ax+a－1的值有正值也有负值，则实数a的取值范围是（ ）
A.a<
B.a>1 C.a<或a>1 D.<a<1
11、若函数f(x)=loga[
－(2a)x]对任意x∈[,+∞]都有意义，则实数a的取值范围是（ ）
A.（0，
B.（0，
） C.
[，1 D.（，）
12、函数f1(x)=
的图象分别是点集C1，C2，C3，C4，这些图象关于直线x=0的对称曲线分别是点集D1，D2，D3，D4，现给出下列四个命题：①D1
D2; ②D1∪D3=D2∪D4; ③D4D3; ④D1∩D3=D2∩D4.
其中，正确命题的序号是（ ）
A.①，③ B.①，② C.③，④ D.②，④
二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中横线上)
13、一条走廊宽 2 m, 长 8 m, 用 6 种颜色的 1
1 m
的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有____________种？
14.甲、乙、丙、丁四人相互传球，首先第一次传球由甲开始，经过7次传球后，球仍回到甲手中的概率是________________（结果用分数表示）
15. 对于定义在R上的函数，有下述四个命题：
①若是奇函数，则
的图象关于点A（1，0）对称；
②若对x∈R，有
，则
的图象关于直线
对称；
③若函数的图象关于直线对称，则为偶函数；
④函数
与函数
的图象关于直线对称。
其中正确命题的序号为 （把你认为正确命题的序号都填上）
16.已知函数f(x)=log
(x2-ax-a)的值域为R，且f(x)在(-∞，1-
)上是增函数，则a的取值范围是__________.
三、解答题(本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分) 设
为正整数，规定：
，已知
．
（1）解不等式：
；
（2）设集合
，对任意
，证明：
；
（3）求
的值；
（4）若集合
，证明：
中至少包含有
个元素．
18. 函数f(x)=loga(x－3a)(a＞0,且a≠1),当点P（x,y)是函数y=f(x)图象上的点时，Q（x－2a,－y)是函数y=g(x)图象上的点.
（Ⅰ）写出函数y=g(x)的解析式.
（Ⅱ）当x∈［a+2,a+3］时，恒有f(x)－g(x)≤1,试确定a的取值范围.
19.(本小题满分12分) 已知在（－1，1）上有定义，
=1，且满足
对数列
（1）证明：在（－1，1）上为奇函数； （2）求
的表达式；
（3）是否存在自然数m，使得对于任意
成立？若存在，求出m的最小值.
20.(本小题满分12分)
已知函数f(x)=x-a，g(x)=x2+2ax+1(a为正常数)，且函数f(x)与g(x)的图象在y轴上的截距相等.
(1)求a的值；
(2)求函数f(x)+g(x)的单调递增区间；
(3)若n为正整数，证明：
21.(本小题满分12分) 某商场以100元/件的价格购进一批羊毛衫，以高于进价的相同价格出售.销售有淡季与旺季之分.标价越高，购买人数越少.我们称刚好无人购买时的最低标价为羊毛衫的最高价格，市场调查发现：
①购买人数是羊毛衫标价的一次函数；
②旺季的最高价格是淡季最高价格的
倍；
③旺季商场以140元/件价格销售时，商场能获取最大利润.
问：在淡季销售时，商场要获取最大利润，羊毛衫的标价应定为多少？
22.(本小题满分14分) 已知
是方程
的两个不等实根，函数
的定义域为
。
（Ⅰ）求
；
（Ⅱ）证明：对于
，若
。
高三数学（文科）（10月）阶段考试题参考答案
制卷人 周祖勇
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | D | A | D | B | C | C | C | A | D | B | G |
13: 
14:
15: ①③ 16:0≤a≤2
17: 解：（1）①当0≤
≤1时，由
≤得，≥
．∴≤≤1．
②当1＜≤2时，因
≤恒成立．∴1＜≤2．
由①，②得，
≤的解集为{≤≤2}．（3分）
（2）∵
，
，
，
∴当
时，
；
当
时，
；
当
时，
．
即对任意
，恒有
．（6分）
（3）
，
，
，
，……
一般地，
（
N）．
(9分)
（4）由（1）知，
，∴
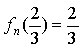．则
．∴
．
由（2）知，对，或1，或2，恒有，∴
．则0，1，2
．
由（3）知，对
，
，
，
，恒有
，∴
，，，．
综上所述，，0，1，2，，，，．∴
中至少含有8个元素．（12分）
18: 解：（Ⅰ）设P(x0,y0)是y=f(x)图象上点，Q（x,y）,则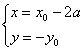
，
∴
∴－y=loga(x+2a－3a)，∴y=loga
(x＞a)
5分
（Ⅱ）
∴x＞3a
∵f(x)与g(x)在［a+2,a+3］上有意义.
∴3a＜a+2 ∴0＜a＜1 6分
∵f(x)－g(x)≤1恒成立
loga(x－3a)(x－a)≤1恒成立.
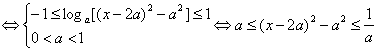8分
对x∈［a+2,a+3］上恒成立，令h(x)=(x－2a)2－a2
其对称轴x=2a,2a＜2,2＜a+2
∴当x∈［a+2,a+3］
hmin(x)=h(a+2)， hmax=h(a+3)
∴原问题等价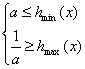
10分
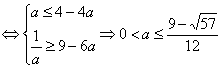12分
19: 解：（1）当x=y=0时，
；令x=0，得
∴对任意的
故在（－1，1）上为奇函数. （4分）
（2）∵
满足
∴
∵
在（－1，1）上为奇函数.
∴
；
由
（8分）
（3）
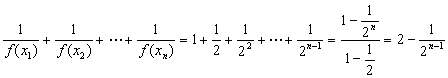
假设存在自然数m，使得对于任意
成立.
即
恒成立. ∴
解得
.
∴存在自然数，使得对于任意
成立.
此时，m的最小值为16. （12分）
20: 解：(1)由题意，得f(0)=g(0),a=1.又a＞0，所以a=1. 2分
(2)解：f(x)+g(x)=x-1+x2+2x+1.
当x≥1时，f(x)+g(x)=x2+3x，它在[1,+
]上单调递增； 3分
当x＜1时，f(x)+g(x)=x2+x+2，它在[-
，1]上单调递增. 5分
又f（x）＋g(x)在x＝1处连续，故它在[-，+）上单调递增
7分
(3)证明：设cn=
，考查数列｛cn｝的变化规律.
解不等式
＜1，由cn＞0，上式化为10·
＜1. 10分
解得n＞
，因n∈N，得n≥4，于是c1≤c2≤c3≤c4，而c4＞c5＞c6＞…，
所以10f(n)·
·
·
. （12分）
21: 解：设在旺季销售时，羊毛衫的标价为
元/件，购买人数为
，
，则旺季的最高价格为
元/件， 利润函数
=
， 
（5分）
由题意知 
即旺季的最高价格是180元/件，则淡季的最高价格是180×
=120（元/件） （7分）
现设淡季销售时，羊毛衫的标价为
元/件，购买人数为
，
则淡季的最高价格为
（元/件），即
利润函数
（10分）
∴
，即
时，
为最大
∴在淡季销售时，商场要获取最大利润，羊毛衫的标价应定为110元/件。（12分）
22: （Ⅰ）设
则
又
故在区间上是增函数。
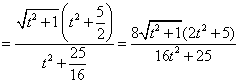（7分）
（Ⅱ）证：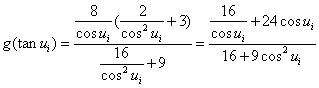
，而均值不等式与柯西不等式中，等号不能同时成立，
（14）分