高三年级第二次摸底考试数学试题（理）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分。考试用时120分钟。考试结束后，将第Ⅱ卷和答题卡一并交回。
第Ⅰ卷（共60分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。不能答在试卷上。
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（A+B）=P（A）·P（B）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，选择一个符合题目要求的选项.
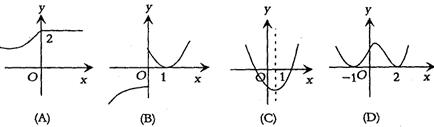
1．在复平面内，复数
对应的点位于 （ ）
|
2．设集合
则 R（A∩B）等于
（ ）
A．R B．
C．{0} D．O
|
4．已知圆C：
，直线
圆上存在两点到直线l的距离为1，则k的取值范围是 （ ）
A．（－17，－7） B．（3，13）
C．（－17，－7）∪（3，13） D．[－17，－7]∪[3，13]
5．已知
= （ ）
A．
B．
C．
D．
6．对于平面
下列命题中真命题是 （ ）
A．若
B．若
|
D．若
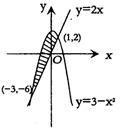
7．如右图，阴影部分的面积是 （ ）
A．
B．
C．
D．
8．已知点O是△ABC所在平面内一点，且
则O是△ABC的 （ ）
A．内心 B．外心 C．垂心 D．重心
9．已知不等式
对任意正实数x，y恒成立，则正实数a的最小值是（ ）
A．2 B．4 C．6 D．8
10．P是双曲线
的右支上一点，F1，F2分别为双曲线的左、右焦点，焦距为2c，则△PF1F2的内切圆的圆心横坐标为 （ ）
A．－a B．a C．－c D．c
11．若数列{an}的通项公式
，数列{an}的最大项为第x项，最小项为第y项，则x+y等于 （ ）
A．3 B．4 C．5 D．6
12．已知函数
且当
，则
的图象的交点个数为（ ）
A．3 B．4 C．5 D．6
第Ⅱ卷（共90分）
二、填空题：本大题共4小题，每小题4分，共16分.答案须填在题中横线上.
|
|
14．将正奇数按一定规律填在5列的数表中，
则第252行，第3列的数是 .
15．过抛物线
与抛物线交于A、B两点，且
△OAB（O为坐标原点）的面积为
=
.
16．已知函数f（x）满足：
+
.
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）
已知a、b、c是△ABC三边长，关于x的方程
的两根之差的平方等于4，△ABC的面积
（Ⅰ）求角C；
（Ⅱ）求a、b的值.
18．（本小题满分12分）
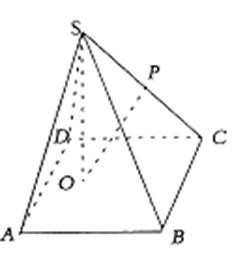
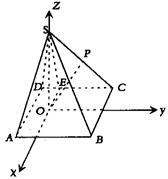
如图，已知四棱锥S—ABCD的底面是边长为4的正方形，S在底面上的射影O落在正方形ABCD内，且O到AB、AD的距离分别为2和1.
（Ⅰ）求证：
是定值；
|
19．（本小题满分12分）
已知数列{an}的前n项和为Sn，且满足
（Ⅰ）判断
是否为等差数列？并证明你的结论；
（Ⅱ）求Sn和an
| |
20．（本小题满分12分）
设
是函数
的两个极值点，且
（Ⅰ）求a的取值范围；
（Ⅱ）求证：
.
21．（本小题满分12分）
甲、乙两公司同时开发同一种新产品，经测算，对于函数f（x）、g（x），当甲公司投入x万元作宣传时，若乙公司投入的宣传费小于f（x）万元，则乙公司对这一新产品的开发有失败的风险，否则没有失败的风险；当乙公司投入x万元作宣传时，若甲公司投入的宣传费小于g（x）万元，则甲公司对这一新产品的开发有失败的风险，否则没有失败的风险。
（Ⅰ）试解释
的实际意义；
（Ⅱ）设
，甲、乙公司为了避免恶性竞争，经过协商，同意在双方均无失败风险的情况下尽可能少地投入宣传费用，问甲、乙两公司各应投入多少宣传费？
22．（本小题满分14分）
椭圆G：
的两个焦点F1（－c，0）、F2（c，0），M是椭圆上的一点，且满足
（Ⅰ）求离心率e的取值范围；
（Ⅱ）当离心率e取得最小值时，点N（0，3）到椭圆上的点的最远距离为
求此时椭圆G的方程；（ⅱ）设斜率为k（k≠0）的直线l与椭圆G相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点
的直线对称？若能，求出k的取值范围；若不能，请说明理由.
| |
参考答案
一、选择题
1．C 2．B 3．C 4．C 5．A 6．C 7．C 8．C 9．B 10．B 11．A 12．D
二、填空题：
13．12
14．2011 15．2 16．30
三、解答题：
17．解：（Ⅰ）设
的两根
则
……………………………………………………………………2分
………………………………………………………………4分
又
……………………………………………………………………6分
（Ⅱ）由
①………………………………………………………………8分
由余弦定理：
即：
②……………………………………………………10分
由①②得：a=8，b=5 ……………………………………………………12分
18．解证：（Ⅰ）在△SDC内，作SE⊥CD交CD于E，连结OE.……………………1分
∵SO⊥平面ABCD， ∴SO⊥CD
∵CD平面SOE
∵CD⊥OE
∴OE//AD
∴DE=1，从而CE=3
|
是定值.
（Ⅱ）以O为坐标原点，以OS所在直线为Oz轴，
以过O且平行于AD的直线为Ox轴，以过O且平
行于AB的直线为Oy轴，建立如图所示的空间直
角坐标系.………………………………7分
于是，A（2，－1，0），B（2，3，0），C（－2，3，0），
S（0，0，3），
………………8分
设点Q（x，y，z），则存在
（这是关键！将点的坐标用一个变量表示）
即
，
得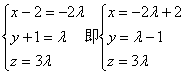
………………………………10分
令
得
…………………………………………………………11分
由
……………………………………………………………………12分
19．解证：（Ⅰ）
………………………………1分
当n≥2时，
………………2分
故是以2为首项，以2为公差的等差数列.…………………………4分
（Ⅱ）由（Ⅰ）得
…………………5分
当n≥2时，
…………………………6分
当n=1时，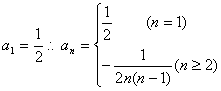
………………8分
（Ⅲ）1°当n=1时，
成立…………………………9分
2°假设n=k时，不等式成立，即
成立
则当n=k+1时，
即当n=k+1时，不等式成立
由1°，2°可知对任意n∈N*不等式成立.
（Ⅲ）另证：
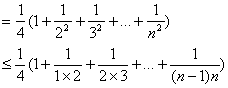
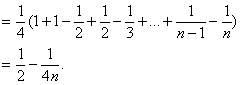
20．解证：（I）易得
…………………………………………1分
的两个极值点
的两个实根，又a＞0
……………………………………………………3分
∴
∵
……………………………………………………7分
（Ⅱ）设
则
由
上单调递增………………10分
………………………………………………12分
21．解：（I）f（0）=10表示当甲公司不投入宣传费时，乙公司要避免新产品的开发有失败风险，至少要投入10万元宣传费；g（0）=20表示当乙公司不投入宣传费时，甲公司要避免新产品的开发有失败的风险，至少要投入20万元宣传费。………………………………4分
（Ⅱ）设甲公司投入宣传费x万元，乙公司投入宣传费y万元，依题意，当且仅当
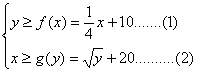成立，双方均无失败的风险……………………8分
由（1）（2）得
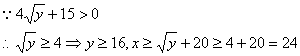
答：要使双方均无失败风险，甲公司至少要投入24万元，乙公司至少要投入16万元。
……………………………………………………………………………………12元
22．解：（I）设M（x0，y0）
①
又
②……………………2分
由②得
代入①式整理得 
又
解得
……………………………………………………………………4分
（Ⅱ）（i）当
设H（x，y）为椭圆上一点，则
若0
由
（舍去）…………………………6分
若b≥3，当y=－3时，HN2有最大值2b2+18
由2b2+18=50得b2=16
∴所求椭圆方程为
……………………………………8分
（ii）设A（x1，y1），B（x2，y2），Q（x0，y0），则由
③
又直线PQ⊥直线l ∴直线PQ方程为
将点Q（x0，y0）代入上式得，
④………………11分
由③④得Q
…………………………………………12分
（解1）而Q点必在椭圆内部 
由此得
故当
时A、B两点关于点P、Q的直线对称.…………14分
（解2）∴AB所在直线方程为
由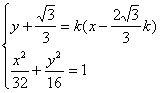
得
显然1+2k2≠0
而
直线l与椭圆有两不同的交点A、B ∴△＞0
解得
故当时，A、B两点关于点P、Q的直线对称。
…………………………………………………………………………14分
（ii）另解；设直线l的方程为y=kx+b
由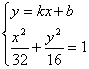
得
设A（x1，y1），B（x2，y2），Q（x0，y0），则
③……………………9分
又直线PQ⊥直线l ∴直线PQ方程为
将点Q（x0，y0）代入上式得， ④………………10分
将③代入④
⑤…………………………………………11分
∵x1，x2是（*）的两根
⑥……12分
⑤代入⑥得
∴当时，A、B两点关于点P、Q的直线对称。
…………………………………………………………………………14分