高三年级第三次六校联考数学试卷
天津塘沽一中、汉沽一中、大港一中、咸水沽一中、杨柳青一中、一百中学
本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分,共150分,考试时间120分钟
第I卷 (选择题，共50分)
注意事项：
1 答第Ⅰ卷前，请考生将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上
2 选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂其它答案，不能答在试卷上
一、选择题（本题共10个小题，每小题5分，共50分 在每小题给出的四个选项中，有且只有一个是正确的）
1 设集合P={直线的倾斜角}，Q={两个向量的夹角}，R={两条直线的夹角}，M={直线l1到l2的角}则必有
A Q
R=PM
B R
MPQ
C Q=RM=P
D RPMQ
2 在等差数列
中，若
，则其前n项和
的值等于5C的是
A 
B 
C 
D 
3 （文）若点B分
的比为
，且有
，则
等于
A ２
B 
C 1
D －1
（理）函数
是
A 周期为
的奇函数
B 周期为的偶函数
C 周期为
的奇函数
D 周期为的偶函数
4 过点（－4，0）作直线L与圆x2+y2+2x－4y－20=0交于A、B两点，如果AB=8，
则L的方程为
A 5x+12y+20=0
B 5x-12y+20=0
C 5x-12y+20=0或x+4=0
D 5x+12y+20=0或x+4=0
5（文）已知p,
q, p+q是等差数列,p ,q ,pq是等比数列，则椭圆
的准线方程是
A 
B 
C 
D 
（理）已知命题P：关于
的不等式
的解集为
；命题Q：
是减函数 若P或Q为真命题，P且Q为假命题，则实数
的取值范围是
A （1，2）
B 
1，2）
C （－
，1
D （－，1）
6 （文）已知命题P：关于的不等式的解集为；命题Q：是减函数 若P或Q为真命题，P且Q为假命题，则实数的取值范围是
A （1，2）
B 1，2）
C （－，1 D （－，1）
（理）若点B分的比为，且有，则等于
A ２
B
C 1
D －1
7 （文）函数
是
A 周期为的奇函数
B 周期为的偶函数
C 周期为
的奇函数
D 周期为的偶函数
（理）若
，对任意实数
都有
，且
, 则实数的值等于
A 
B 
C -3或1 D -1或3
8（文）若
，对任意实数都有
，且, 则实数的值等于
A 
B 
C -3或1 D -1或3
（理）设函数
，数列是公比为的等比数列，若
则
的值等于
A -1974
B -1990
C 2022
D 2038
9 （文）设函数，数列是公比为的等比数列，若则的值等于
A -1974
B -1990
C 2022
D 2038
（理）函数
是奇函数，且在R上是增函数的充要条件是
A p>0 ,q=0
B p<0 ,q=0
C p≤0，q＝0 D p≥0，q=0
10 （文）函数是奇函数，且在R上是增函数的充要条件是
A p>0 ,q=0
B p<0 ,q=0
C p≤0，q＝0 D p≥0，q=0
（理）已知函数
满足：①
；②在
上为增函数
若
,且
,则
与
的大小关系是
A 
B 
C 
D 无法确定
第Ⅱ卷 (非选择题，共100分)
注意事项：
1 第Ⅱ共6页，用蓝、黑色的钢笔或圆珠笔直接答在试卷中
2 答卷前，请将密封线内的项目填写清楚
二、填空题：本大题共6小题，每小题4分，共24分 请把答案填在题后的横线上
11（文）命题“若
，则
”的否命题为
（理）如果椭圆的对称轴为坐标轴，短轴的一个端点与两焦点组成一正三角形，焦点在y轴上，且a－c=,
那么椭圆的方程是
12 （文）
的值是
（理）函数
的反函数
是
13 （文）如果椭圆的对称轴为坐标轴，短轴的一个端点与两焦点组成一正三角形，焦点在y轴上，且a－c=,
那么椭圆的方程是
（理）已知直线ax+by+c=0被圆M：
所截得的弦AB的长为
，那么
的值等于
14 已知直线ax+by+c=0被圆M：所截得的弦AB的长为，那么
的值等于
15 已知函数
设
，则使
成立的
的范围是
16 有 以下几个命题
①曲线
按
平移可得曲线
；
②若x+y
，则使x+y取得最大值和最小值的最优解都有无数多个；
③设A、B为两个定点，为常数，
，则动点P的轨迹为椭圆；
④若椭圆的左、右焦点分别为F1、F2，P是该椭圆上的任意一点，则点F2关于“
的外角平分线”的对称点M的轨迹是圆
其中真命题的序号为
;（写出所有真命题的序号）
三、解答题：本大题6小题，共76分 解答应写出文字说明，证明过程或演算步骤
17 (本题满分12分)
（文）如图，已知圆A的半径是2，圆外一定点N与圆A上的点的最短距离为6，
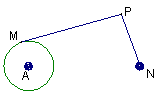过动点P作A的切线PM（M为切点），连结PN使得PM：PN=
，试建立适当的坐标系，求动点P的轨迹
（理）设有关于x的不等式
a
(I)当a=1时，解此不等式
(II)当a为何值时，此不等式的解集是R
18 (本题满分12分)
（文）已知
,求
和
的值
（理）已知二次函数
的二次项系数为，且不等式
的解集为
（I）若方程
有两个相等的实数根，求的解析式；
(II)若函数
的无极值，求实数的取值范围
19 (本题满分12分)
（文）设有关于x的不等式a
(I)当a=1时，解此不等式
(II)当a为何值时，此不等式的解集是R
（理）如图，已知圆A的半径是2，圆外一定点N与圆A上的点的最短距离为6，
过动点P作A的切线PM（M为切点），连结PN使得PM：PN=，试建立适当的坐标系，求动点P的轨迹
20 (本题满分12分)
（文）已知二次函数的二次项系数为，且不等式的解集为
（I）若方程 有两个相等的实数根，求的解析式；
(II)若函数的无极值，求实数的取值范围
（理）已知向量
，向量
与向量
的夹角为
，且
（I）求向量
（II）若向量与向量
的夹角为
，向量
，其中A,C为△ABC的内角，且B=600，求
的取值范围
21 (本题满分14分)
已知数列{an}的前n项和为Sn，且an=(3n+Sn)对一切正整数n成立
（I）证明：数列{3+an}是等比数列，并求出数列{an}的通项公式；
（II）设
，求数列
的前n项和Bn；
（III）数列{an}中是否存在构成等差数列的四项？若存在求出一组；否则说明理由
22 (本题满分14分)
如图，已知椭圆
过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D，设
①求
的解析式；
②求的最值
天津市高三年级第三次六校联考
数学试卷
参考答案
一、选择题：(本大题共10小题,每小题5分,共50分)
1 B 2 A 3 文C（理C） 4
D 5 文A（理B） 6 文B（理C） 7 文C（理C） 8 文C（理A） 9 文A （理D） 10 文D（理A）
二、填空题：（本大题共6小题，每小题4分，共24分 ）
11 （文）“若
，则
” ，（理）
12 （文）
，（理）
，
13 （文），（理）－2
14
-2 15 
16 ②④
三、解答题：（本大题共6个解答题，满分76分，）
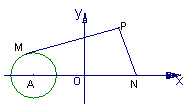
17 （文）解：以AN所在直线为x轴，AN的中垂
线为y轴建立平面直角坐标系如图所示，
则A(-4,0),N(4,0),设P（x，y） 
由PM：PN=，PM2=PA2 –MA2得：
代入坐标得：
整理得：
即
所以动点P的轨迹是以点
（理）解：(I)当a=1时 
或
或
或
(II)原不等式
设
有
当且仅当
即
时
依题有：10a<10 ∴
为所求
18 （文）解：
解得
若由方程组
解得
，可参考给分
（理）解：(Ⅰ)设
（a≠0），则
…… ①
…… ②
又∵
有两等根
∴
…… ③
由①②③得
又∵
∴a<0, 故
∴
(Ⅱ)
∵g(x)无极值
∴方程
得
19 （文）解：(I)当a=1时
或或
或
(II)原不等式
设有
当且仅当
即时
依题有：10a<10 ∴为所求
（理）解：以AN所在直线为x轴，AN的中垂
线为y轴建立平面直角坐标系如图所示，
则A(-4,0),N(4,0),设P（x，y）
由PM：PN=，PM2=PA2 –MA2得：
代入坐标得：
整理得：
即
所以动点P的轨迹是以点
20 （文）解：(Ⅰ)设 （a≠0），则
…… ①
…… ②
又∵有两等根
∴…… ③
由①②③得
又∵
∴a<0, 故
∴
(Ⅱ)
∵g(x)无极值
∴方程
得
（理）解：（I）设
（1）
又
故
（2）
由（1），（2）解得
（II）由向量与向量的夹角为得
由
及A+B+C=知A+C=
则
由0<A<得
，得
故的取值范围是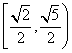
21 解：（I）由已知得Sn=2an-3n，
Sn+1=2an+1-3(n+1),两式相减并整理得：an+1=2an+3
所以3+ an+1=2（3+an），又a1=S1=2a1-3，a1=3可知3+
a1=6
，进而可知an+3
所以
，故数列{3+an}是首相为6，公比为2的等比数列，
所以3+an=6
,即an=3(
)
（II）
设
（1）
（2）
由（2）-（1）得
（III）假设数列{an}中存在构成等差数列的四项依次为:
am1，am2，am3，am4，（ m1<m2<m3<m4 ）
则 3(
)+(
)=3(
)+3(
)
即
+ 
=
+
上式两边同时除以得：1+
故数列{an}中不存在构成等差数列的四项
22 解：（I）依题有：
∴椭圆的左焦点为F（－1，0）故直线方程为：y=x+1
又椭圆的准线方程为
∴A(-m2,-m2+1), D(m2,m2+1) 
由方程组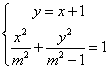
得
成立
又∵A、B、C、D都在直线y=x+1上
∴AB=xB－xA
又∵
∴
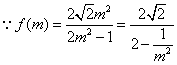
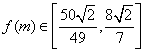
∴当m=2时的最大值为
，
当m=5时的最小值为