高三年级第三次月考数学试题(理)
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.每题均为单项选择题,请从A、B、C、D四个答案中选出你认为正确的一个填入答题卡中.
1.已知全集U={1, 2, 3, 4, 5},集合A, ![]() ,若
,若![]() ,
,![]() {2, 5},则B=( )
{2, 5},则B=( )
A.{2, 4, 5} B.{2, 3, 5} C.{3, 4, 5} D.{2, 3, 4}
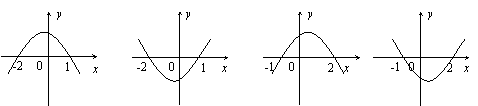 2.不等式
2.不等式![]() 的解集为
的解集为![]() ,则函数
,则函数![]() 的图象大致为( )
的图象大致为( )
A B C D
3.条件![]() ,条件
,条件![]() ,则p是q的 ( )
,则p是q的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
|
A.![]()
B.![]()
C.![]()
D.![]()
5. 若函数![]() 内单调递减,则f(x)可以是 ( )
内单调递减,则f(x)可以是 ( )
A.1 B.![]() C.
C.![]() D.
D.![]()
6.设平面向量![]()
![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在数列![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.5 C.
B.5 C.![]() D.1
D.1
8.不等式![]() 上恒成立,则实数a的取值范围是 ( )
上恒成立,则实数a的取值范围是 ( )
A.![]() B.(1,2
B.(1,2![]() C.
C.![]() D.
D.![]()
9. 已知函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.爷爷与奶奶给他们的孙女、孙子们(孙女与孙子人数不等)分糖果吃,爷爷分配方案如下:给每个孙女的糖果数等于他们孙子的人数,给每个孙子的糖果数等于他们孙女的人数,而且若如此分配糖果恰好分完。可实际分配时,奶奶记反了,她给每个孙女的糖果数等于他们孙女的人数,而给每个孙子的糖果数等于他们孙子的人数。请问:分配结果如何 ( )
A.刚好分完 B.不够分
C.分后有剩余 D.上述三种情况均有可能
11.甲、乙、丙三位学生用计算机联网学习数学,每天上课后独立完成6道自我检测题,甲及格的概率为![]() ,乙及格的概率为
,乙及格的概率为![]() ,丙及格的概率为
,丙及格的概率为![]() ,三人各自检测一次,则三人中只有一人及格的概率为 ( )
,三人各自检测一次,则三人中只有一人及格的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
12.已知抛物线![]() 在点(2,-1)处与直线
在点(2,-1)处与直线![]() 相切,则
相切,则![]() 的值为( )
的值为( )
A.20 B.-2 C.9 D.2
|
|
14.一个等差数列共有2n-1(n∈N,n>1)项,若该数列的各项和为2008,且an=8,则n=
15.若函数![]() 的最小正周期是
的最小正周期是![]() =
=
| |
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本题12分)
已知![]() ,求
,求![]() 的值
的值
18.(本题12分)已知函数![]() ,且
,且![]() ,且
,且![]() 的定义域为[0, 1]
的定义域为[0, 1]
(1)求![]() 的表达式;(2)判断
的表达式;(2)判断![]() 的单调性并加以证明;(3)求
的单调性并加以证明;(3)求![]() 的值域.
的值域.
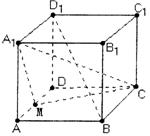
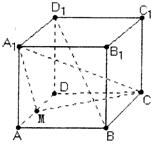
|
(1)求证:AD∥平面A1BC;
(2)求证:平面A1MC⊥平面A1BD1;
(3)求点A到平面A1cMC的距离.
20.(本题12分)某市2003年共有1万辆燃油型公交车。有关部门计划于2004年投入128辆电力型公交车,随后电力型公交车每年的投入比上一年增加50%,试问:
(1)该市在2010年应该投入多少辆电力型公交车?
(2)到哪一年底,电力型公交车的数量开始超过该市公交车总量的![]()
(参考数据:1.56 = 11.4,1.57 = 17.1,1.58 = 25.6)
21.(本题满分12分)已知函数![]() ,其中a为大于零的常数.
,其中a为大于零的常数.
(1)求函数![]() 的定义域;
的定义域;
(2)若对任意![]() ,
, ![]() ,恒有
,恒有![]() ,试确定a的取值范围.
,试确定a的取值范围.
22.(本题14分)已知定义在![]() , 1)上的函数
, 1)上的函数![]() 满足
满足![]() ,且对x,
,且对x, ![]() , 1)时有:
, 1)时有:![]()
(1)判断![]() 在
在![]() , 1)上的奇偶性并证明之;
, 1)上的奇偶性并证明之;
(2)令![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)设Tn为数列![]() 的前n项和,问是否存在正整数m,使得对任意的
的前n项和,问是否存在正整数m,使得对任意的![]() ,
,
| |
参考答案
一、选择题:本大题共12个小题,每小题4分,共48分。在每小题给出的四个选项中,只有一项是符合题目要求的。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | A | C | D | A | B | A | C | B | C | B |
二、填空题:本大题共4小题,每小题4分,共16分。
11.(1,+∞) 12.126 13.4 14.(0,2] 15.14
三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤。
17.-![]()
18.(1)∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
故![]() 即为所求
即为所求
(2)![]() 在[0, 1]内单调递减
在[0, 1]内单调递减
设x1, x2为[0, 1]内任意两个实数且x1<x2
则![]()
![]()
∵![]() ∴
∴![]()
∴![]() 故
故![]() 从而
从而![]()
|
(3)∵![]() ∴值域为
∴值域为![]() , 0]
, 0]
19.解法一:(1)由已知:AD∥BC,
而BC在平面A1BC内,AD在平面A1BC外
所以,AD∥平面A1BC
(2)连结BD
由![]() ,
,
得△DAB ~△CDM, ∴∠ADB =∠DCM,
又∠DCM +∠DMC = 90°
∴∠ADB +∠DMC = 90°
故BD⊥CM,
又BD是BD1在平面ABCD的射影,
由三垂线定理可知:BD1⊥CM
同理可得BD1⊥A1M,
∴BD1⊥平面A1MC, 又![]() 平面A1BD1
平面A1BD1
∴平面A1MC⊥平面A1BD1
(3)取BC的中点P,设O为A1C与BD1的交点,OC的中点Q,连结AP、PQ,
由AP∥MC知点A到平面A1MC的距离等于点P到平面A1MC的距离,
由P、Q分别是BC、OC的中点知PQ∥BO,![]() ,
,
又BO⊥平面A1MC, ∴PQ⊥平面A1MC,而BO =
a, ![]() ,
,
即点A到平面A1MC的距离为![]() .
.
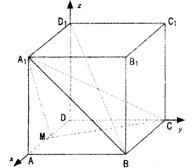
解法二:以D为原点,以射线DA、DC、DD1分别为x、y、z的正半轴建立空间直坐标系,可知各点坐标分别为D(0,0,0),![]()
|
(1)由此可知![]() ,
,
![]() ,所以
,所以![]()
故![]() ∥
∥![]() ,
,
而BC在平面A1BC内,AD在平面A1BC外
所以AD∥平面A1BC
(2)![]() ,
,
故BD⊥CM.
同理可得BD1⊥A1M,
∴BD1⊥平面A1MC, 又![]() 平面A1BD1
平面A1BD1
∴平面A1MC⊥平面A1BD1
(3)![]() ,由(2)知
,由(2)知![]() 是平面A1MC的法向量,
是平面A1MC的法向量,
∴点A到平面A1MC的距离为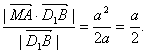
20.解:(1)设2004年为第一年,其电力型公交车的数量为a1 = 128,第n年的电力型公交车的数量为an辆依题意可知{an}为a1 = 128,q = 1.5的等比数列,
2004年a1 = 128,
2005年a2 = 128×1.5,…
2010年![]() (辆)
(辆)
(2)记![]() ,依据题意,得
,依据题意,得![]()
于是![]() (辆),即
(辆),即![]() ,
,
因此![]()
所以,到2011年底,电力型公交车的数量开始超过该市公交车总量的![]()
21.(1)由![]() 得
得![]()
方程![]() 的根的判别式
的根的判别式![]()
当![]() 时
时![]() ∴
∴![]() 恒成立,故
恒成立,故![]() ;
;
当![]() 时
时![]() 此时方程
此时方程![]() 的根为
的根为![]()
且![]() 故
故![]() 或
或![]()
综上,当![]() 时,函数的定义域为
时,函数的定义域为![]() ;
;
当![]() 时,函数的定义域为
时,函数的定义域为![]() 或
或![]() }
}
(2)当![]() ,
, ![]() 时,恒有
时,恒有![]() 成立.
成立.
即:![]() 对
对![]() ,
, ![]() 恒成立
恒成立
令![]() (
(![]() ,
, ![]() ) 故
) 故![]()
故当![]() 时,对任意
时,对任意![]() ,
, ![]() 恒有
恒有![]() 成立.
成立.
22.(1)![]() 为奇函数,令
为奇函数,令![]() ,∴
,∴![]()
又当![]() 时
时 ![]() 即:
即:![]() .
.
故![]() 为奇函数.
为奇函数.
(2)∵![]() 满足
满足![]() ,
,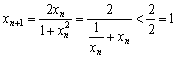
∴![]() ∴
∴![]()
而由(1)知,![]() 在
在![]() , 1)上为奇函数
, 1)上为奇函数
∴![]() ∴
∴![]() 即
即![]()
∴![]() 是以
是以![]() 为首项,以公比为2的等比数列
为首项,以公比为2的等比数列
∴![]()
(3)![]()
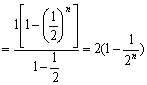
假设存在正整数m,使得对于任意的![]() ,有
,有![]() 成立,
成立,
即:![]() 对一切
对一切![]() 恒成立.
恒成立.
只需![]() 即
即![]() .
.
故存在正整数m,使得对![]() 恒有
恒有![]() 成立,
成立,
此时m的最小值为10