高三年级第四次模考数学(文科)试题
(总分:150分 时间:120分钟)
第Ⅰ卷
一. 选择题:(本大题共12小题,每小题5分,共60分).
1.集合M=![]() ,N=
,N=![]() ,则
,则![]() =( )
=( )
A .M B. N C. R D. ![]()
2.. 函数![]() 的值域是
( )
的值域是
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
3.已知向量![]() 平行,则m等于
( )
平行,则m等于
( )
A.-2 B.2 C.![]() D.
D.![]()
4.使关于![]() 的不等式
的不等式![]() 有解的实数
有解的实数![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,则
的图象,则
f (x)是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知函数![]() (b为常数),若
(b为常数),若![]() 时,
时,![]() 恒成立,则( )
恒成立,则( )
A..b = 1 B.b< 1 C.![]() D.
D.![]()
7.设函数![]() 的导函数
的导函数![]() ,则数列
,则数列![]() 的前n项的和为( )
的前n项的和为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x-1,那么不等式f(x)<![]() 的解( )
的解( )
A.{x0<x<![]() } B.{x-
} B.{x-![]() <x<0}
C.{x-
<x<0}
C.{x-![]() <x<0或0<x<
<x<0或0<x<![]() } D.{xx<-
} D.{xx<-![]() 或0≤x<
或0≤x<![]() }
}
9. 命题p:若![]() 的充分而不必要条件:命题q:函数
的充分而不必要条件:命题q:函数
![]() 的定义域是
的定义域是![]() 则( ) ( )
则( ) ( )
 A.“p或q”为假 B.“p且q”为真
A.“p或q”为假 B.“p且q”为真
C.p真q假 D.p假q真
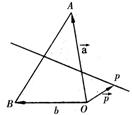
10.如图,![]() 是平面上三点,向量
是平面上三点,向量![]()
![]() ,
,![]()
![]() .
.
在平面![]() 上,
上,![]() 是线段
是线段![]() 垂直平分线上任意一点,
垂直平分线上任意一点,
向量![]() =
=![]() ,且
,且![]() 则
则 ![]() 的值是:( )
的值是:( )
|
 A.
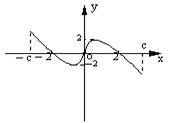
A.11.f(x)是定义在[-C,C]上的奇函数,其图象如下,
令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是( )
A.若a<0,则函数g(x)的图象关于原点对称
|
C.若a≠0,b=2,则方程g(x)=0有两个实根
D.若a≥1,b<2,则方程g(x)=0有三个实根
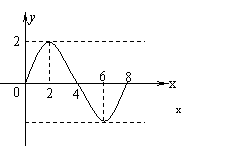 12、已知函数
12、已知函数![]() 的部分图象如图所示, 记
的部分图象如图所示, 记![]() 则
则![]() 的值为( )
的值为( )
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共4小题,每小题4分,共16分)
13.已知![]() 与
与![]() 的夹角为
的夹角为![]() ,若向量
,若向量![]() 与
与![]() 垂直, 则m= 。
垂直, 则m= 。
 14. 不等式
14. 不等式![]() 解集是
解集是
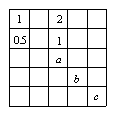
15.在右面的表格中,每格填上一个数字后使每一横行成等差数列,
每一纵列成等比数列,则![]() __ 。
__ 。
16.给出下列命题:
(1)如果命题P:“x>2”是真命题,则Q:x≥2是真命题;
(2)函数![]() 是奇函数,且在(-1,0)∪(0,1)上是增函数;
是奇函数,且在(-1,0)∪(0,1)上是增函数;
(3)“![]() ,且
,且![]() ”的充分不必要条件是“(
”的充分不必要条件是“(![]() ”;
”;
(4)如果等差数列![]() 的前n项的和是
的前n项的和是![]() ,等比数列
,等比数列![]() 的前n项的和是
的前n项的和是![]() ,则
,则![]() 、
、
![]() 、
、![]() 成等差数列,
成等差数列,![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
其中正确命题的序号是: .
三、解答题(本大题共6小题,共76分)
17.(本小题满分12分)已知A,B,C是三角形![]() 三内角,向量
三内角,向量![]() ,且
,且![]()
(Ⅰ)求角![]() ;
;
(Ⅱ)若![]() ,求
,求![]()
18.已知函数f(x)=sin(2x-)+2sin2(x-) (x∈R)
(Ⅰ)求函数f(x)的最小正周期 ; (2)求使函数f(x)取得最大值的x的集合.
19.(本小题满分12分)
已知函数![]() ,点
,点![]() 在
在![]() 上,且
上,且![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,若
,若![]() 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
20、(本小题满分12分)
已知![]() 的反函数为
的反函数为![]() .
.
(1)若![]() ,求x的取值范围D ;
,求x的取值范围D ;
(2)设函数![]() ,当x∈D时,求函数
,当x∈D时,求函数 ![]() 的值域.
的值域.
21.(本小题满分12分)
已知一列非零向![]()
(1)证明:![]() 是等比数列;
是等比数列;
(2)求向量![]()
(3)设![]() 一列,记为
一列,记为![]() 为坐标原点,求点
为坐标原点,求点![]() 的坐标。
的坐标。
22. (本小题满分14分)
设![]() 是定义在R上的奇函数,
是定义在R上的奇函数,![]() 与
与![]() 的图象关于直线x = 1对称,当
的图象关于直线x = 1对称,当![]() 时,
时,![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)当x = 1时,![]() 取得极值,证明:对任意x1、
取得极值,证明:对任意x1、![]() ,不等式
,不等式![]() 。
。
(3)若![]() 是
是![]() 上的单调函数,且当
上的单调函数,且当![]() 时有
时有![]() ,
,
证明:![]() 。
。
高三数学第四次模考答案
一.选择题:BBCAB DADDB BC 13.-5 14。(0,2] 15。1 16。(1)
17解:(Ⅰ)∵![]() ∴
∴![]() 即
即![]()
![]() ,
, ![]()
∵![]() ∴
∴![]() ∴
∴![]() 。。。。。。6分
。。。。。。6分
(Ⅱ)由题知![]() ,整理得
,整理得![]()
∴![]() ∴
∴![]() ∴
∴![]() 或
或![]()
而![]() 使
使![]() ,舍去 ∴
,舍去 ∴![]() …………… 12分
…………… 12分
18.解:(Ⅰ) f(x)=sin(2x-)+1-cos2(x-)
= 2[sin2(x-)- cos2(x-)]+1 =2sin[2(x-)-]+1
= 2sin(2x-) +1
∴ T==π。。。。。。6分
(Ⅱ)当f(x)取最大值时, sin(2x-)=1,有 2x- =2kπ+
即x=kπ+ (k∈Z) ∴所求x的集合为{x∈Rx= kπ+ , (k∈Z)}.… 12分… 12分
19.解(I)![]() .
.
………………………………(1分)
∵点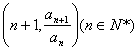 在反函数图像上,
在反函数图像上,![]() ……………………………(3分)
……………………………(3分)
![]()
(II)![]() …………(8分)
…………(8分)
![]() …………(10分)
…………(10分)
又Sn关于n是单调函数,![]() ……
……
20、(文科)解析:∵ ![]() ,∴
,∴ ![]() .
.
(1)∵![]() 即
即![]() .
.
∴![]() ,∴
,∴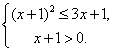 解之得
解之得
![]() , ∴
, ∴![]() . ………………6分
. ………………6分
(2) ∵ ![]()
![]()
![]()
![]() .
. ![]()
令![]() ,显然在[0,1]递增,
,显然在[0,1]递增,
则有![]() .∴
.∴![]() ,
,
即![]() 的值域为
的值域为![]() . ………………12分
. ………………12分
20.(理科)解:(1)![]()
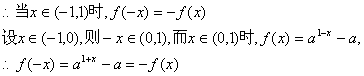
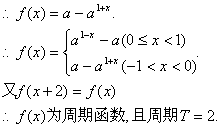
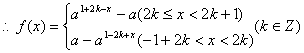 …………………………6分
…………………………6分
(2)当![]()

由函数的周期性可知:![]() …………………………12分
…………………………12分
21、解:(1)![]()
![]() ………………2分
………………2分
首项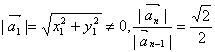 为常数,
为常数, ![]() 是等比数列.………3分
是等比数列.………3分
(2)![]()
![]() ,…………………………5分
,…………………………5分
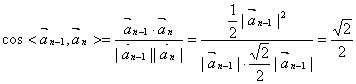 ,
,
![]() 的夹角为
的夹角为![]() ……… ………6分
……… ………6分
(3)![]()
![]()
![]()
![]() … ……8分
… ……8分
由题意可得,![]()
![]() ………………………9分
………………………9分
设![]()
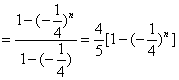 …………………10
…………………10
![]()
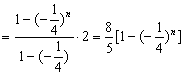
(或![]() )∴点
)∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() )…………………12分
)…………………12分
22.(文科)解:①∵![]() 与
与![]() 的图象关于直线x = 1对称
的图象关于直线x = 1对称
当![]() 时,设
时,设![]() 为
为![]() 上的点
上的点
∴P关于x = 1对称点![]() 则
则![]()
∴![]()
∴![]() ……………………………………………………(3分)
……………………………………………………(3分)
又∵![]() 在R上是奇函数,∴
在R上是奇函数,∴![]() 又设
又设![]() ∴
∴![]()
∴![]() ∴
∴![]()
∴![]() ……………………………………………………(3分)
……………………………………………………(3分)
∴![]() ……………………………………………………(4分)
……………………………………………………(4分)
②![]() ∴
∴![]() ,∴
,∴![]()
∴![]()
∵![]() 有
有![]()
∴![]()
∴![]() 即
即![]() 在(-1,1)上为单调减函数,在
在(-1,1)上为单调减函数,在![]() 上有
上有
![]()
![]() …………………………………………(6分)
…………………………………………(6分)
则![]() 上恒有:
上恒有:![]() …………(8分)
…………(8分)
③若![]() 在
在![]() 单调递减,则
单调递减,则![]()
∴![]()
![]() 上不恒成。
上不恒成。
故a不存在,∴![]() 在
在![]() 递增
递增
∴![]() 在
在![]() 上恒成立。
上恒成立。
∴![]() ………………………………………………………………………………(9分)
………………………………………………………………………………(9分)
不妨假设![]() ,则
,则![]()
已知![]() 矛盾
矛盾
若![]() 则
则![]()
与![]() (矛盾)
(矛盾)
∴综上可知![]() ……………………………………………………………(14分)
……………………………………………………………(14分)
22.(理科)(1)![]()
(i)![]() 符合要求;
符合要求;
(ii)a<0时,令g(x)=ax2+x-1, x→+∞,g(x)→-∞,
故f(x)在![]() 只能是单调递减的.
只能是单调递减的.
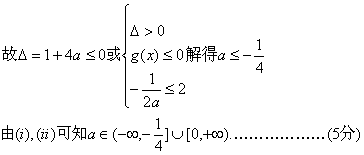
(2)![]()
故![]() …………………………………………………………(8分)
…………………………………………………………(8分)
(3)反证法:不妨设![]()
|
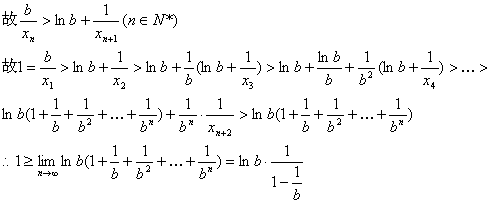
又由(2)当b>1时, 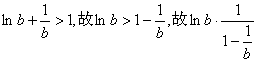 >1与①矛盾.
>1与①矛盾.
故![]() ……………………(14分)
……………………(14分)