![]()
![]() 高三年级数学学科第二次月考试卷
高三年级数学学科第二次月考试卷
本卷共150分 考试时间120分钟
一、选择题:(每题5分,共50分;在每小题给出的四个选项中,恰有一项是符合题目要求的)
1.已知![]() 是等差数列,且
是等差数列,且![]() ,
,![]() ,此数列的首项与公差依次(A)
,此数列的首项与公差依次(A)
A、19,-2 B、21,-2 C、15,-1 D、16,-1
2.求![]() 的值(B)
的值(B)
A、![]() B、-
B、-![]() C、
C、![]() D、-
D、-![]()
3.已知A是三角形的内角,且sinA+cosA=![]() ,则cos2A等于(B)
,则cos2A等于(B)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.在等比数列![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() 的值为 (C)
的值为 (C)
A、3或-3 B、 3 C、 -3 D、不存在
5.若一个等差数列前2项的和为10,最后2项的和为110 ,且所有项的和为390 ,则这个数列有 (D)
A、10项 B、11项 C、12项 D、13项
6.若a>1,![]() ;则函数
;则函数![]() 的图象一定不经过 (B)
的图象一定不经过 (B)
A、第一象限 B、第二象限 C、第三象限 D、第四象限
7.若f (x)=x5-ax3+bx+2,且 f (-5)=17;则f (5)的值为(D)
A、19 B、13 C、-19 D、-13
8.已知![]() 则
则![]() 等于(A)
等于(A)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9.已知函数![]() ,f(x)>0的解集为
,f(x)>0的解集为![]() ,则函数
,则函数![]() 的图象(C)
的图象(C)
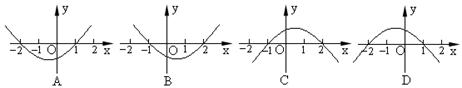
10.某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入a元定期储蓄,若年利率为p且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将所有的存款及利息全部取回,则可取回的钱的总数(元)为(不计利息税) (D)
A、![]() B、
B、
![]()
C、![]() D、
D、![]()
二、填空题:(本大题共6小题,每小题5分,共30分.)
11.函数![]() 的最小正周期是
的最小正周期是![]() .
.
12.已知![]() ,则函数
,则函数![]() 的最大值为
的最大值为![]()
13.已知函数![]() 是奇函数,当
是奇函数,当![]() 时,f(x)=x(1+x),则
时,f(x)=x(1+x),则![]() 时f(x)=_x(1-x)_.
时f(x)=_x(1-x)_.
14.数列![]() 中,
中,![]() ,则
,则![]() 10100.
10100.
15.数列{an}为等差数列,Sn为其前n项和,已知a3=12,S10>0,S11<0,则Sn的最大值为60.
16.下列命题:
① 若数列{an}的前n项和是Sn=n2+2n-1,则{an}为等差数列;
② 若数列{an}的前n项和是Sn=3n-c,则c=1是{an}为等比数列的充要条件;
③ 等比数列{an}中,a1+a2=1,a3+a4=9,那么a4+a5=27;
函数f (x)=xx+bx+c,当b=0,c>0时,方程f (x)=0只有一个实根;其中正确的命题是:②④
![]()
![]() 高三年级数学学科第二次月考答题纸
高三年级数学学科第二次月考答题纸
一、选择题:(每题5分,共50分;在每小题给出的四个选项中,恰有一项是符合题目要求的)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | B | C | D | B | D | A | C | D |
二、填空题:(本大题共6小题,每小题5分,共30分.)
11.![]() .
12.
.
12. ![]() 13. f(x)=_x(1-x)_.
13. f(x)=_x(1-x)_.
14. ![]() 10100.
15. 60. 16. ②④.
10100.
15. 60. 16. ②④.
三、解答题:(本大题共5小题,共70分)
17.(本小题12分,第一、二两小问满分各6分)
设关于![]() 的不等式
的不等式![]()
![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() .(1)求集合A,B;
.(1)求集合A,B;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
17.解:⑴由于![]() ……… 3分
……… 3分
由![]() 得,
得,![]() …………..4分
…………..4分
![]()
![]() 6分
6分
⑵![]()
![]() …………………8分
…………………8分
![]()
![]() …………………………10分
…………………………10分
![]() ……………………………12分
……………………………12分
18.(12分)某单位建造一间地面面积为12平方米的背面靠墙的长方体小房,房屋正面的造价为1200元每平方米,房屋侧面的造价为800元每平方米,屋顶的造价为5800元。如果墙的高为3米,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低,最底的总造价为多少元?
18.解:设底面矩形中与墙相对的边长为xm,则另一边的长为![]() m,又设房屋的总造价为k元,则……………………………2分
m,又设房屋的总造价为k元,则……………………………2分 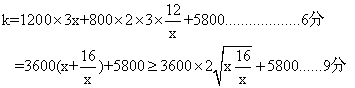
当且仅当![]() ,即x=4时,k最小。………11分
,即x=4时,k最小。………11分
因此,当底面矩形中与墙相对的边长时4m,另一边长为3m时,房屋的 总造价最低。最低造价为34600元。………12分
19. (本小题满分16分,每一小问满分4分)
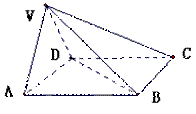 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(1)证明AB⊥平面VAD;
(2)求面VAD与面VDB所成的二面角的大小;
(3)若AB=2,求四棱锥V-ABCD的体积;
(4)求D点到平面VAB的距离。
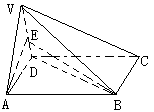
证明:(1)证明:
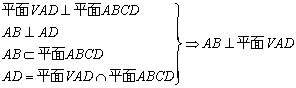 ...4分
...4分
(2)解:取VD的中点E,连结AE,BE,...5分
∵△VAD是正三形,
∴AE⊥VD,AE=![]()
∵AB⊥平面VAD, ∴AB⊥AE.又由三垂线定理知BE⊥VD. ...6分
因此,tan∠AEB=![]() ...7分
...7分
即得所求二面角的大小为![]() ...8分
...8分
(3)解:取AD的中点F,连结VF,...9分
∵△AVD是正三形, ∴VF⊥AD,VF=![]() =
=![]() ...10分
...10分
又∵平面VAD⊥底面ABCD,且平面VAD![]() 底面ABCD=AD
底面ABCD=AD
∴VF⊥底面ABCD. ... . ... . ... . ... . ... . ... . ... . ... . ... . ... . ... . ...11分
∴VV-ABCD=![]() . . ... . ... . ... . ... . ... . ...12分
. . ... . ... . ... . ... . ... . ...12分
(4)解:连接BF. . ... . ... . ... . ... . ... . ...13分
易求BF=![]() ,VB=2
,VB=2![]() ,所以S三角形VAB=2
,所以S三角形VAB=2
∵VV-ABD= VD-VAB=![]() =
=![]() ... . ... . ... . ... . ... . ...15分
... . ... . ... . ... . ... . ...15分
∴h=![]() .即D到平面VAB的距离是
.即D到平面VAB的距离是![]() ... . ... . ... . ... . ... . ...16分
... . ... . ... . ... . ... . ...16分
20.(本题共14分)
数列![]() 时其前n项和Sn满足
时其前n项和Sn满足![]()
①求证:![]() 是等差数列。
是等差数列。
②设![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
20.解:①当![]() 时
时 ![]()
∴![]() ………5分
………5分
∴![]() 构成以
构成以![]() 为首项公差为2的等差数列
为首项公差为2的等差数列
∴![]() ∴
∴![]() …………9分
…………9分
②![]() …………11分
…………11分
∴![]() ……14分
……14分
21.(本小题共16分)已知函数:![]() .
.
(1)当![]() 的定义域为
的定义域为![]() 时,求证:
时,求证:![]() 的值域为
的值域为![]() ;
;
(2)设函数![]() ,求
,求![]() 的最小值 .
的最小值 .
(1)证明:![]() ,
,
当![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
即![]() 的值域为
的值域为![]() . ………………4分
. ………………4分
(2)![]()
①当![]() .
.
如果![]() 即
即![]() 时,则函数在
时,则函数在![]() 上单调递增,
上单调递增,
∴![]() ; ………………6分
; ………………6分
若![]() ;
………………8分
;
………………8分
当![]() 时,
时,![]() 最小值不存在.
………………9分
最小值不存在.
………………9分
②当![]() ,
,
如果![]() ;
………11分
;
………11分
如果![]()
![]() ……………………13分
……………………13分
当![]() .
.
![]() .…………………15分
.…………………15分
综合上述:1。当![]() 时, g(x)最小值是
时, g(x)最小值是![]() ;
;
2。当![]() 时, g(x)最小值是
时, g(x)最小值是![]() ;
;
3。当![]() 时, g(x)最小值为
时, g(x)最小值为![]() ;
;
4。当![]() 时, g(x)最小值不存在.…………………16分
时, g(x)最小值不存在.…………………16分