高三年级数学综合训练(一)
试卷
总分150分
一.选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数![]() 的反函数为( )
的反函数为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2.函数![]() 在区间
在区间![]() 上存在反函数的充要条件是 ( )
上存在反函数的充要条件是 ( )
A、![]() 或
或![]() B、
B、![]() 或
或![]() C、
C、![]() D、
D、![]()
3. 函数![]() 在其定义域上单调递减,且值域为
在其定义域上单调递减,且值域为![]() ,则它的反函数的值( )
,则它的反函数的值( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知双曲线![]() 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为![]() 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.已知实数![]() 同时满足(1)
同时满足(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,则
,则![]() 的最大值是
( )
的最大值是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6.P是△ABC所在平面上一点,若![]() ,则P是△ABC的 (
)
,则P是△ABC的 (
)
A 外心 B 内心 C 重心 D 垂心
7.若一系列函数的解析式和值域相同,但定义域互不相同,则称这些函数为“同族函数”,例如函数![]() ,
,![]() 与函数
与函数![]() ,
,![]() 即为“同族函数”。下面4个函数中,能够被用来构造“同族函数”的是 ( )
即为“同族函数”。下面4个函数中,能够被用来构造“同族函数”的是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8.设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
(1)![]() (2)
(2)![]() (3)
(3)![]()
(4)![]() ,其中,假命题是( )
,其中,假命题是( )
A、(1)(2) B、(2)(3) C、(1)(3) D、(2)(4)
9. 已知不等式![]() 对任意正实数
对任意正实数![]() 恒成立,则正实数
恒成立,则正实数![]() 的最小值
的最小值
为 ( )
(A)8 (B)6 (C)4 (D)2
10. 当![]() 时,函数
时,函数![]() 的 ( )
的 ( )
A、最小值是![]() B、最大值是
B、最大值是![]() C、最小值是4 D、最大是4
C、最小值是4 D、最大是4
二.填空题:本大题共6小题,每小题5分,共30分。把答案填在答题卡的相应位置
11.若三点![]() 共线,则
共线,则![]() 的值等于_________________.
的值等于_________________.
12.双曲线![]() 上的点到左焦点的距离与到左准线的距离的比是3,则
上的点到左焦点的距离与到左准线的距离的比是3,则![]() 等于
等于
13.设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() =14,
=14,![]() -
-![]() =30,则
=30,则![]() = .,
= .,
14. 如果函数![]() 满足:对任意实数
满足:对任意实数![]() 都有
都有![]() ,且
,且![]() ,则
,则![]() ______________________.
______________________.
15. 三棱柱ABC-![]() 中,所有棱长均为1,则点B
中,所有棱长均为1,则点B![]() 到平面ABC
到平面ABC![]() 的距离为 .
的距离为 .
16. 设![]() ,
,![]() 是两个不共线的向量,若
是两个不共线的向量,若![]() ,
,![]() ,
,![]() ,且
,且![]() 三点共线,则
三点共线,则![]() _______
_______
三.解答题:本大题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17. (本题12分)已知![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() ,设点
,设点![]() 是棱
是棱![]() 上的动点(不含端点),过点
上的动点(不含端点),过点![]() 的平面交棱
的平面交棱![]() 于点
于点![]()
(1)求证:![]()
(2)求二面角![]() 的大小(结果用反正弦函数值表示)
的大小(结果用反正弦函数值表示)
(3)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,试说明理由
,试说明理由
18.(本题14分)已知点A、B、C的坐标分别为A(3,0),B(0,3),C(cosα,sinα),![]() 。
。
(1)若![]() ,求角α的值;
,求角α的值;
| |
19.(本小题满分14分)
设数列{an}的各项都是正数,Sn是其前n项和,且对任意n∈N*都有a![]() =2Sn-an.
=2Sn-an.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=(2n+1)![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
20. (本题满分14分) 如图已知F1、F2为
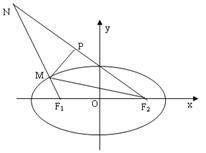 椭圆
椭圆![]() 的两焦点,M是椭圆上一点,
的两焦点,M是椭圆上一点,
延长F1M到N,P是NF2上一点,且满足
![]() ,
,![]() ,点N的轨迹方程为
E。
,点N的轨迹方程为
E。
⑴求曲线E的方程;
⑵过F1的直线l交椭圆于G,交曲线E于H,
(G、H都在x轴上方),若![]() ,
,
求直线l的方程;
21、(本小题满分16分)已知函数![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的定义域、值域都是
的定义域、值域都是![]() ,若存在,则求出
,若存在,则求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ,求m的取值范围.
,求m的取值范围.
参考答案:
一、1—5 BACCB , 6—10 DADCC
二、11.![]() 12.
12.![]() 13.77
13.77![]() 14.4012 15.
14.4012 15.![]() 16.- 8
16.- 8
17.(1)![]() ,又
,又![]() ,
,
![]()
(2)连结![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,又
,又![]() ,面
,面![]() 面
面![]()
![]() ,
,![]() ,
,![]() 是二面角
是二面角![]() 的平面角,不妨设
的平面角,不妨设![]()
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,
中,![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]()
(3)假设棱![]() 上存在点
上存在点![]() ,由题意得
,由题意得![]() ,要使
,要使![]() ,只要
,只要![]() 即可
即可
当![]() 时,
时,![]() 中,
中,![]() ,
,
![]()
![]() ,
,![]() 时,
时,![]()
18.解:解:(1)∵![]() =(cos
=(cos![]() -3, sin
-3, sin![]() ),
), ![]() =(cos
=(cos![]() , sin
, sin![]() -3).
-3).
∴∣![]() ∣=
∣=![]() 。
。
∣![]() ∣=
∣=![]() 。
。
由∣![]() ∣=∣
∣=∣![]() ∣得sin
∣得sin![]() =cos
=cos![]() .又∵
.又∵![]()
![]() ,∴
,∴![]() =
=![]()
(2)由![]() ·
·![]() =-1,得(cos
=-1,得(cos![]() -3)cos
-3)cos![]() +sin
+sin![]() (sin
(sin![]() -3)=-1
-3)=-1
∴ sin![]() +cos
+cos![]() =
=![]() .①
.①
又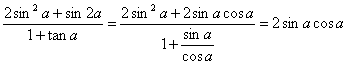 .
.
由①式两边平方得1+2sin![]() cos
cos![]() =
=![]() , ∴2sin
, ∴2sin![]() cos
cos![]() =
=![]() ,
,
∴![]()
19.(本小题满分12分)
解:(Ⅰ)∴a![]() =2Sn-an,n∈N*,
=2Sn-an,n∈N*,
∴当n=1时,a![]() =2a1-a1,即a
=2a1-a1,即a![]() =a1
=a1
∵a1>0 a1=1. …1分
又a![]() ,
,
∴a![]() -a
-a![]() ,
,
即(an+1-an)
![]() ,
,
从而an+1-an=1. …4分
故数列{an}是1为首项,公差为1的等差数列.
∴an=n. …6分
(Ⅱ)由(Ⅰ)知:bn=(2n+1)![]() =(2n+1)2n.
=(2n+1)2n.
∴Tn=b1+b2+…+bn=3×2+5×22+…+(2n+1)2n ①
∴2Tn=3×22+5×23+…+(2n-1)2n+(2n+1)2n+1 ②
①—②得-Tn=3×2+2×22+2×23+…+2×2n-(2n+1)2n+1
=6-(2n+1)2n+1+![]()
=-(2n-1)2n+1-2… 11分
故Tn=(2n-1)2n+1+2.… 12分
20.解:⑴由已知得F1(-1,0)
∵![]() ,
,![]() =0
=0
∴MP为线段NF2的垂直平分线
∴│MN│=│MF2│ …3分
由椭圆的定义知:│MF1│+│MF2│=2![]()
∴│NF1│=│MN│+│MF1│=│MF2│+│MF1│=2![]()
显然M为椭圆左、右端点时不满足![]() =0
=0
∴曲线E的方程为(x+1)2+y2=8 (y≠0)
⑵由⑴知│F1H│=2![]()
∵![]() =2
=2![]() ∴G为线段F1H的中点
∴G为线段F1H的中点
∴│F1G│=![]() │F1H│=
│F1H│=![]()
∴G点的轨迹是以F1(-1,0)为圆心,![]() 为半径的圆的x轴上半部分
为半径的圆的x轴上半部分
∴G点轨迹方程是(x+1)2+y2=2 (y>0)
又∵G在椭圆上:![]() =1
=1
由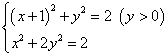 解得
解得 ![]()
∴G(0,1) …13分
∴所求的直线方程为:y=x+1
21、解:(1)∵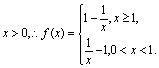
∴![]() 在(0,1)上为减函数,在(1,+∞)上是增函数.
在(0,1)上为减函数,在(1,+∞)上是增函数.
由![]() ,可得
,可得![]() ,即
,即![]() .
.
∴![]() …3分
…3分
故![]() ,即
,即![]() …4分
…4分
(2)不存在满足条件的实数![]() .
.
若存在满足条件的实数![]() ,使得函数
,使得函数![]() 的定义域、值域都是[
的定义域、值域都是[![]() ],则
],则![]() .
. 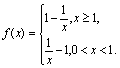
①当![]() ∈(0,1)时,
∈(0,1)时,![]() 在(0,1)上为减函数.
在(0,1)上为减函数.
故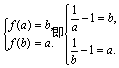 解得
解得![]() .
.
故此时不存在适合条件的实数![]() .…6分
.…6分
②当![]() ∈
∈![]() 时,
时,![]() 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
故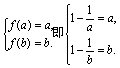
此时![]() 是方程
是方程![]() 的根,由于此方程无实根.
的根,由于此方程无实根.
故此时不存在适合条件的实数![]() .…8分
.…8分
③当![]() ∈(0,1),
∈(0,1),![]() 时,由于1∈[
时,由于1∈[![]() ],而
],而![]() ,故此时不存在适合条件的实数
,故此时不存在适合条件的实数![]() .
.
综上可知,不存在适合条件的实数![]() .…10分
.…10分
(3)若存在实数![]() ,使得函数
,使得函数![]() 的定义域为[
的定义域为[![]() ]时,值域为
]时,值域为![]() ,则
,则![]() .
.
①当![]() ∈(0,1)时,由于
∈(0,1)时,由于![]() 在(0,1)上是减函数,值域为
在(0,1)上是减函数,值域为![]() ,
,
即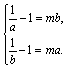 解得a=b>0,不合题意,所以
解得a=b>0,不合题意,所以![]() 不存在.
不存在.
②当![]() 时,由(2)知0在值域内,值域不可能是
时,由(2)知0在值域内,值域不可能是![]() ,所以
,所以![]() 不存在. 故只有
不存在. 故只有![]() .
.
∵![]() 在(1,+∞
)上是增函数,∴
在(1,+∞
)上是增函数,∴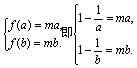
![]() 是方程
是方程![]() 有两个根.
有两个根.
即关于x的方程![]() 有两个大于1的实根.
有两个大于1的实根.
设这两个根为![]() .
.
则![]() ∴
∴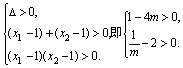
解得![]() .…14分
.…14分
综上m的取值范围是![]() .
.